基于车辆被拒绝概率的停车区服务水平研究

刘大任 林航飞

（同济大学交通运输工程学院 上海 201804）

0 引 言

随着城市汽车保有量的快速增长，停车需求也在不断增加．在一些城市的商业区，由于缺乏有效的诱导信息，人们有时需要转换多个停车场才能寻找到车位．限于交通状况和停车场的布局，一旦车辆第一次进入的停车场已经饱和，人们往往就需要绕行较长的距离才能到达下一个停车场，从而为出行带来很大的不便．因此，车辆能否不经转换而直接寻找到车位从一个方面反映了区域停车设施的服务水平．

为了对区域停车设施进行系统考虑，在此将区域内若干个空间上互补的停车场称为一个停车区．目前关于停车区服务水平的研究还较少，沈旗等［1］从投资者与使用者的角度建立了面向多个停车场的评价体系；其他一些研究则更多地针对单一的停车场，如蔡家明［2］、董红彦［3］等．而现行的相关规范则主要是对停车场泊位数、场址、出入口数量以及一些具体几何参数的规定，并没有涉及服务水平的内容［4－5］．本文针对包含2个停车场的停车区，建立了车辆首次寻找车位被拒绝概率的计算模型，通过算例分析了相关因素对这一概率的影响，以期为评价停车区的服务水平提供新的角度和方法，为停车设施规划与诱导信息发布提供参考．

1 车辆首次寻找车位被拒绝的概率计算模型

车辆能否直接寻找到车位与停车区的泊位供给和停车需求有关．对应不同的供给与需求，车辆在首次寻找车位时被接受或被拒绝的可能性也不同．设某区域的停车区由A，B 2个停车场组成，车辆进入该区域后可任选其一进行停车．如图1所示，其中黑色区域表示停车点．2个停车场的泊位数分别记为nA，nB车位；该停车区已停泊的车辆数记为x，辆．根据A，B中停放的车辆数，可以将这x辆车在2个停车场的分布分成若干种情形，每一种情形又有不同的车辆组合，每一种组合对应一种可能的分布结果．

图1 研究区域示意图

现作如下2点假设：（1）这x辆车在2个停车场内随机分布，即每一种组合对应的分布结果以相等的概率出现；（2）第（x＋1）辆车首次寻找车位时随机地选择A，B 2个停车场，其概率pA＝pB＝1／2．

若第（x＋1）辆车进入某停车场时，该停车场已满，则定义该辆车首次寻找车位被拒绝，其概率记为Pr．

根据nA，nB的关系，可以分成如下2种情况：

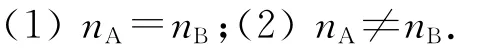
对于这2种情况，车辆首次寻找车位被拒绝的情形有所不同，分析如下．

1．1 2 个停车场泊位数相等时的情况

在2停车场泊位数相等时，不妨设nA＝nB＝n．对x值进行分段考虑．

1）当x＜n时，停车场A，B均未饱和，故第（x＋1）辆车首次寻找车位被拒绝的概率Pr＝0．

2）当n≤x≤2n时，该停车区已停的x辆车在A，B 2个停车场可能的分布情形见表1（按A中车辆数依次递增、B中车辆数依次递减排序，下同）．

表1 停车区已有车辆分布表

在表1中共存在（2n－x＋1）种情形．在第1种情形中，停车场B达到饱和；在第（2n－x＋1）种情形中，停车场A达到饱和．只有这两种情形有可能使下一辆车首次寻找车位时被拒绝．由于假定这x辆车在两个停车场内随机分布，则第i种情形出现的概率．根据全概率公式［6］可知，此时

1．2 2 个停车场泊位数不等时的情况

在2停车场泊位数不等时，设nA＝m＜nB＝n．同理，对x值进行分段考虑．

1）当x＜m时，停车场A，B均未饱和，故Pr＝0．

2）当m≤x＜n时，这x辆车在A，B 2个停车场可能的分布情形见表2．

表2 停车区已有车辆分布表

此时，只有在第（m＋1）种情形中停车场A达到饱和，可能使下一辆车首次寻找车位时被拒绝

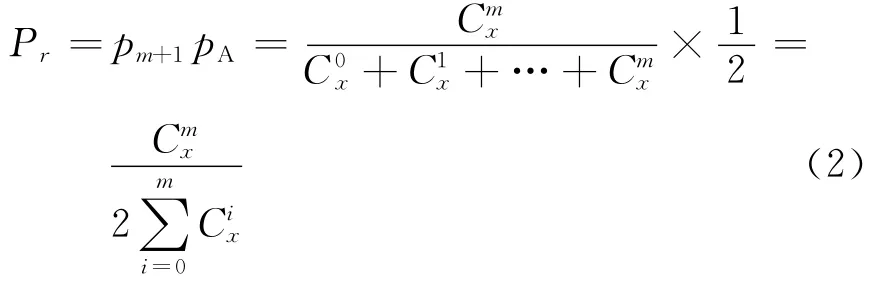
3）当n≤x≤m＋n时，这x辆车在A，B中可能的分布情形见表3．

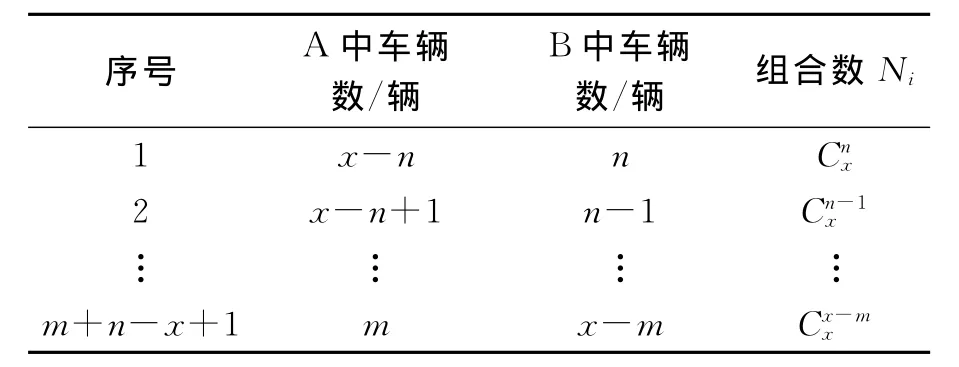
表3 停车区已有车辆分布表

在表3中共存在（m＋n－x＋1）种情形．在第1种情形中，停车场B达到饱和；在第（m＋n－x＋1）种情形中，停车场A达到饱和．只有这两种情形有可能使下一辆车首次寻找车位时被拒绝．此时

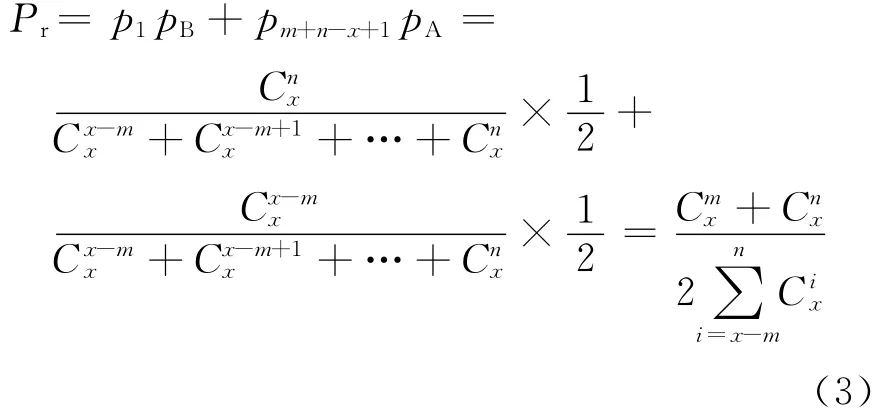
由前面的计算模型可以看出，车辆首次寻找车位被拒绝的概率Pr与2个停车场的泊位数nA，nB以及这两个停车场中已停放的车辆数x有关．如果记停车区容量为C，车位；2个停车场的泊位数之比为k；停车区饱和度为S；定义

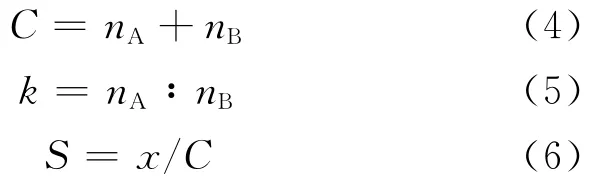
那么可以将Pr的影响因素归结为3个停车区的参数：C，k，S．由此可以通过上述模型，探讨这3个因素对车辆首次寻找车位被拒绝概率的影响．

2 算例分析

为探讨停车区容量C，各停车场泊位数配比k以及停车区饱和度S对Pr的影响，现在依次选择其中一个变量为定值，探讨Pr与另外2个变量的关系．依据前面的计算模型，分别计算各组数据对应的Pr值，根据计算结果绘制曲线，进行算例分析．

1）选定C＝120，k值分别取1∶1，1∶1．5，1∶2，1∶3，绘制Pr随S的变化曲线（见图2）．

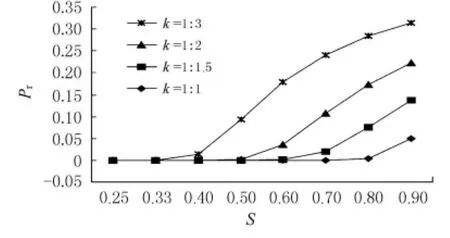
图2 C为定值时P r与k，S关系图

由图2可见，对于该组所选取的数据，在C值一定时，对应任意一个k值，Pr随S的增大而单调上升（Pr＝0的区间除外）；Pr曲线在某些k值下会出现凸凹性的变化，以k＝1∶3时为例，Pr在0．25≤S≤0．60的区间加速上升，在0．60≤S≤0．90的区间上升趋缓（由于所取的S值并不连续，这里对拐点的准确位置不作探讨）；在相同的饱和度下，k值越接近于1，Pr越小，即在停车区容量一定的情况下，均衡设置2个停车场的泊位数可以减小车辆首次寻找车位被拒绝的概率．

2）选定k＝1∶1．5，S分别取0．5，0．6，0．7，0．8，绘制Pr随C的变化曲线（见图3）．

图3 k为定值时P r与C，S关系图

由图3可见，对于该组所选取的数据，在k值一定时，对应任意的S值，随着C的增大，Pr值单调递减，且其减小的速度在放缓；对于任意的C值，S越大，那么S每增加0．1，Pr的增量就越大，即在停车区饱和度较大的情形下，饱和度的继续增加会对用户产生显著的影响．

3）选定S＝0．8，k值分别取1∶1，1∶1．5，1∶2，1∶3，绘制Pr随C的变化曲线，见图4．

图4 S为定值时P r与C，k关系图

由图4可见，对于该组所选取的数据，在S值一定时，对应任意的k值，随着C的增大，Pr值单调减小；对应k＝1∶1，1∶1．5，1∶3这三条曲线，随着C值不断增大，Pr值减小的速度在放缓，而对应k＝1∶2这条曲线，在C由80增加到160时，Pr值下降平缓，C由160增加到200时，Pr值又有了相对显著的下降；不同的k值对应的曲线有明显的间隔，说明k对Pr有显著影响，均衡设置互补停车场的泊位数对用户更为有利．

3 结束语

停车区的服务水平涉及到安全性、便利性以及费用等诸多因素，本文从车辆寻找车位被拒绝的概率这一角度对其进行了探讨，建立了车辆首次寻找车位被拒绝概率的计算模型并进行了算例分析．结果表明，停车区容量、区内各停车场泊位数的配比以及停车区饱和度对这一概率有显著影响，均衡设置两个停车场的泊位数可以减小车辆首次寻找车位被拒绝的概率．本文为评价停车区服务水平提供了一个新的视角，可为停车设施的规划以及相应的规范制定提供参考．同时，车辆寻找车位被拒绝的概率这一信息可以作为未来停车诱导信息的一个组成部分，以更好地均衡各个停车场的需求、提高停车设施的服务水平．

应当指出的是，只有在每辆车均随机进入2个停车场时，车辆的分布结果才是随机的；当停车区已有车辆数超过某个停车场的泊位数时，如果一个停车场达到饱和，后续车辆就无法随机进入2个停车场，此时车辆并非随机分布．因此本文所做假设有一定的不合理之处，对于模型计算结果的偏差有待进一步测定，同时对于车辆在多个停车场的分布规律尚需进一步研究．

［1］沈 旗，李 平．停车场评价指标体系和双层规划模型［C］／／程代展，段广仁．第25届中国控制会议论文集（下册）．北京：北京航空航天大学出版社，2006：1 705－1 708．

［2］蔡家明．城市停车场模糊评价研究［J］．上海工程技术大学学报，2009，23（4）：304－307．

［3］董红彦，王秋平．基于模糊理论的停车场服务水平评价［J］．交通科技与经济，2009（6）：14－17．

［4］中华人民共和国建设部．JGJ100－98汽车库建筑设计规范［S］．北京：北京建筑工程学院出版社，1999．

［5］中华人民共和国公安部，建设部．停车场规划设计规则（试行）［S］．北京：中华人民共和国公安部，1989．

［6］同济大学概率统计教研组．概率统计［M］．3版．上海：同济大学出版社，2004．