城市交通的多方法综合评价与分析＊

傅新平 邱 超 周习鹏

（水路公路交通安全控制与装备教育部工程研究中心1） 武汉 430063）（武汉理工大学智能交通系统研究中心2） 武汉 430063）

1 评价指标体系的建立

城市交通综合评价指标应该满足宏观和微观两方面进行评价的要求．同时，评价指标还要获取方便、计算简单．在参考大量相关文献的基础上，充分考虑城市交通系统的设施建设、功能建设、结构建设、环境和安全特性［1－3］，利用德尔菲法选定交通发展指数、交通畅通指数、交通环境指数、交通安全指数和交通出行指数5个准则层及万人拥有公交车数量、车均机动车道面积、道路网密度、车均停车面积、人均非机动车道路面积、主干道平均车速、道路平均饱和度、交叉口阻塞率、城市中心区干路网交通负荷度、单位运输量燃油消耗、日均空气质量等级、万车死亡率、万车事故率、万人死亡率、公交分担率、私家车分担率、出租车分担率、非机动车分担率共18个指标，运用层次分析法（analysis hierarchy process，AHP）建立城市交通综合评价指标的体系．见表1．

2 确定评语集

根据公安部交管局、建设部城建司2007年联合印发的《城市道路交通管理评价指标体系》，把指标的指数评价划分为5个等级，即［10，9］，［9，8］，［8，7］，［7，6］，［6，0］5个区间，对应的评语集为：｛V1，V2，V3，V4，V5｝：｛很好，较好，一般，差，很差｝．相应评语集的百分制表示为C＝｛c1，c2，c3，c4，c5｝＝｛100～90，90～80，80～70，70～60，60～50｝．

表1 城市交通综合评价指标体系

3 指标权重的确定

3．1 主观赋权法——层次分析法确定权重

层次 分 析 法 （analysis hierarchy process，AHP）确定权重的步骤首先是构造判断矩阵B，然后分别是层次单排序一致性检验和层次总排序一致性检验，通常认为当层次总排序随机一致性比例CR≤0．10时，层次总排序的计算结果具有满意的一致性［4－5］．层次分析法最主要的判断矩阵B的确定受主观因素影响很大，而判断矩阵直接关系后续工作能否正常进行，故为了削弱主观因素影响，应该将之与客观赋权法结合使用．

3．2 客观赋权法——熵值法确定权重

熵值法（entropy method）确定权重的步骤如下．

2）计算第i项指标的熵值ei＝－ ×ln（pij），其中：k ＝ ［ln（n）］－1为常数，显然，0≤ei≤1．

3）计算指标xi的差异性系数di＝1－ei，di越大，则指标对系统的比较作用越大．

4）确定指标权重wi＝

3．3 组合赋权法确定权重

设pi，qi分别为主、客观赋权法确定的指标xi的权重，则可以用以下两个公式来确定综合权重wi，分别称为“加法”集成法式（1）和“乘法”集成法式（2）．

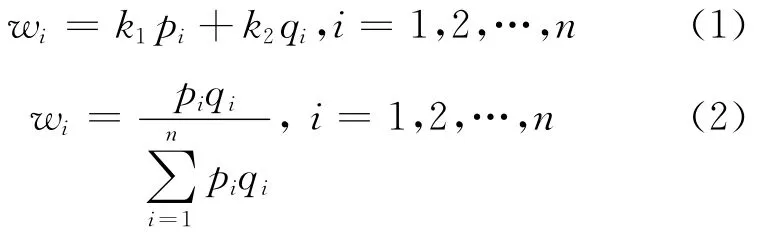
鉴于“加法”集成法中系数k1，k2难于确定，故本文选用“乘法”集成法．

3．4 构造评价矩阵R

评价矩阵R是反映从评价因素U到评价尺度V之间的模糊评价关系，是一种模糊映射．本文采用灰色关联法确定评价矩阵R［6］．首先确定样本矩阵D，然后确定评估灰类，即确定评估灰类的定级数、灰类的灰数及灰数的白化权函数．依据实际评估问题设评估灰类序号为e（e＝1，2，…，g），即有g个评估灰类，通常的白化权函数有以下3种：

1）第1灰类 “高”（e＝1），灰数为⊗∈［d1，∞），其白化权函数为

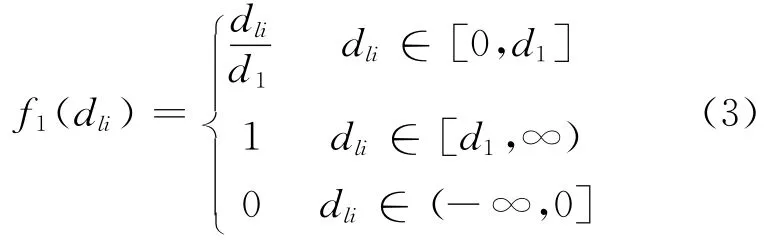
2）第二灰类 “中”（e＝2），灰数为⊗∈［0，d2，2d2］，白化权函数为

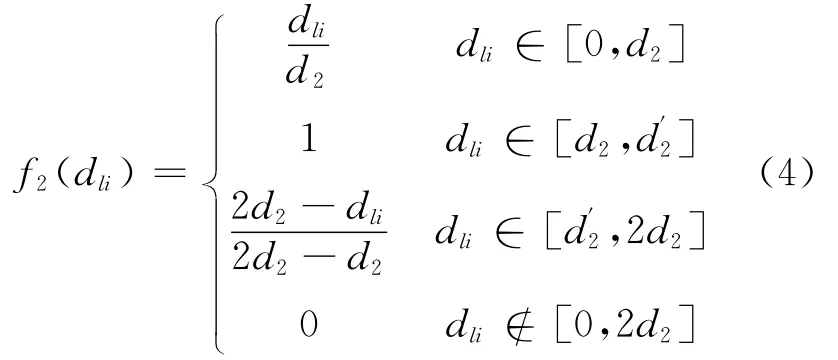
3）第三灰类 “低”（e＝3），灰数为⊗∈［0，d3，2d3］，白化权函数为

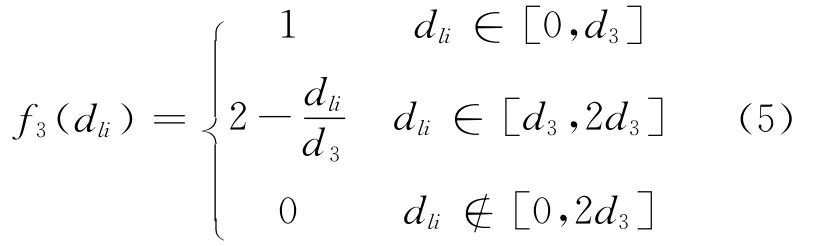
白化权函数的阈值di（i＝1，2，…，n），可采用客观阈值或相对阈值或二者的综合来确定．用灰色统计法确定灰数的白化权函数，求出dli属于第e类评估标准的权fe（dli），据此求出评判矩阵的灰色统计数（记为pie）和总灰色统计数（记为pi）

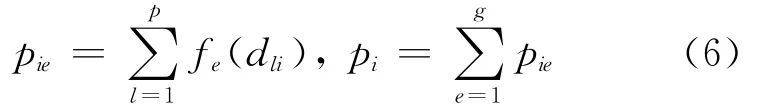
再综合r位专家对第s个评估对象的评估指标，采用第e种评估标准的灰色权值rie＝pie／pi，进而可构成评价矩阵

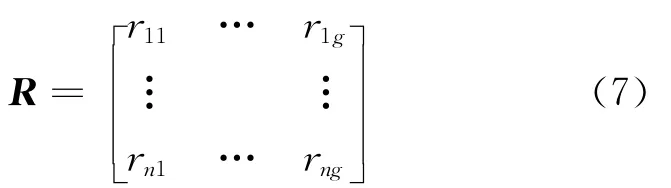
4 城市交通模糊综合评价

综合评价就是将各指标的组合权重与评价矩阵R，进行多次模糊计算，算出最终评语集A，最后对评语进行定量化处理得出综合评价的百分数［7］．

4．1 城市交通模糊综合评价的数学模型

设因素论域U 由k层组成（k≥2），第一层（最高层）具有m个因素，U＝，，…，），评语集V＝（V1，V2，…，Vn），则多层次模糊综合评价的数学模型为

式中：W为各层的权向量，其中下标的个数x表示W为第x＋1层的各个权向量；R为最底层（第k层）的模糊评价矩阵；运算符“·”按M（∧，∨）运算．

4．2 模糊综合评价的步骤

多层次模糊综合评价是从最底层（第k层）开始，向上逐层运算，第k层评价的结果就是第k－1层因素的模糊关系矩阵，直至得到最后的评语集A＝W·R．然后对评语进行定量化处理得到最终的评价结果．计算步骤如下（k＝2）．

1）城市交通综合评价的因素集分为一级指标集Ui（i＝l，2，3，4，5）和二级指标集Uij（i＝1，2，3，4，5；j＝l，2，3，4，5）．利用 Delphi法和白化权函数法计算出最底层因素集与评语集之间对应的模糊评价矩阵Rij．

2）进行第二层的运算，分别得到Ai＝Wi·Ri，即A1＝W1·R1，…，，Am＝Wm·Rm．完成第二层的计算后，令R ＝ ［A1，A2，…，Am］T．

3）进行最高层的运算，得到最后的评语集A＝W·R，然后对评语进行定量化处理得到最终的评价结果．

4）结果量化处理．评语集采用百分制表示，就得到了一个关于评语的分数向量C＝（c1，c2，c3，c4，c5），对于难以决策的向量，通过分数向量计算得分，令

由于各评语的得分是一个区间，所以一般计算3个有代表性的得分S高，S中，S低．

5 实例应用

以武汉市为例，指标评价值参考《2009年武汉市交通年度发展报告》以及城市建设统计资料，并结合公安部交管局、建设部城建司2007年印发的《城市道路交通管理评价指标体系》．由于“城市中心区干路网交通负荷度”这项指标数据难以获得，故选取其他17项指标对武汉市城市交通系统进行综合评价．请8位专家为上述各项指标打分，规定打分范围为1～10分，得到专家对指标的评价样本矩阵D＝（die）8×17：

将样本矩阵D中的数据分别按照AHP法、熵值法和组合赋权法步骤计算，得各级指标权重如表2、表3所列．

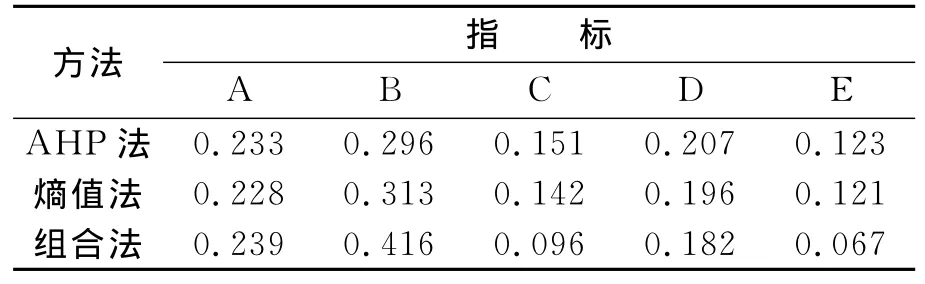
表2 武汉市城市交通综合评价体系一级指标权重

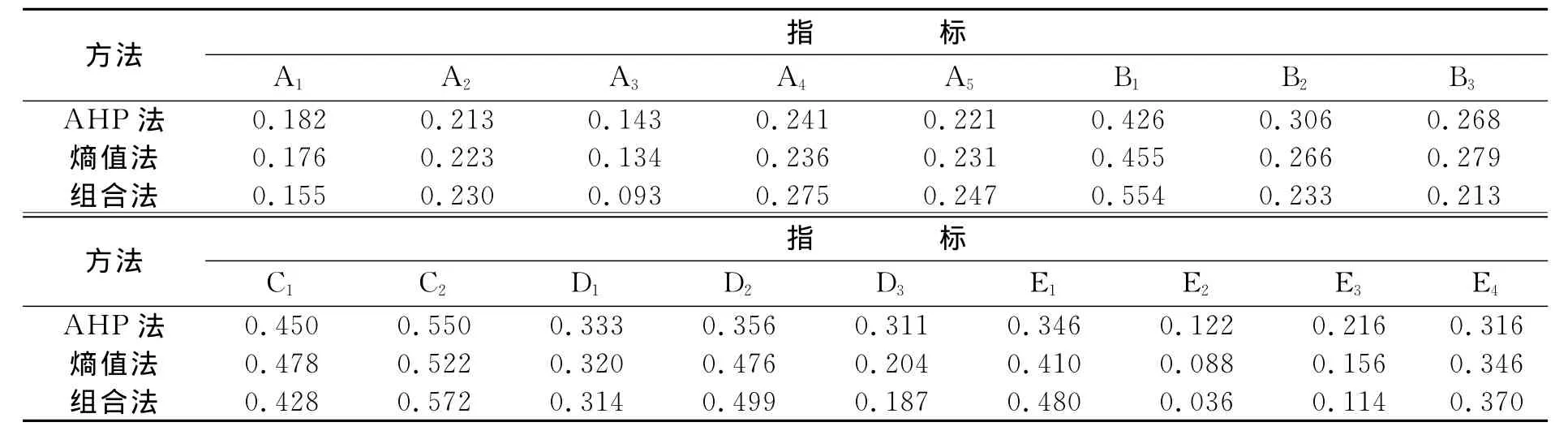
表3 武汉市城市交通综合评价体系二级指标权重

如前所述，把指标的指数评价划分为5个等级，即［10，9］，［9，8］，［8，7］，［7，6］，［6，0］五个区间，对应的评语集为：｛V1，V2，V3，V4，V5｝：｛很好，较好，一般，差，很差｝，即评价灰类为5个．

依照前面介绍的方法，由式（16）、（17）可得pie，pi和rei（i＝1，2，…，17；e＝1，2，…，5），于是得R＝（rie）5×17矩阵

由评价矩阵R，按最大隶属度原则，对二级指 标进行模糊评价，如表4所列．

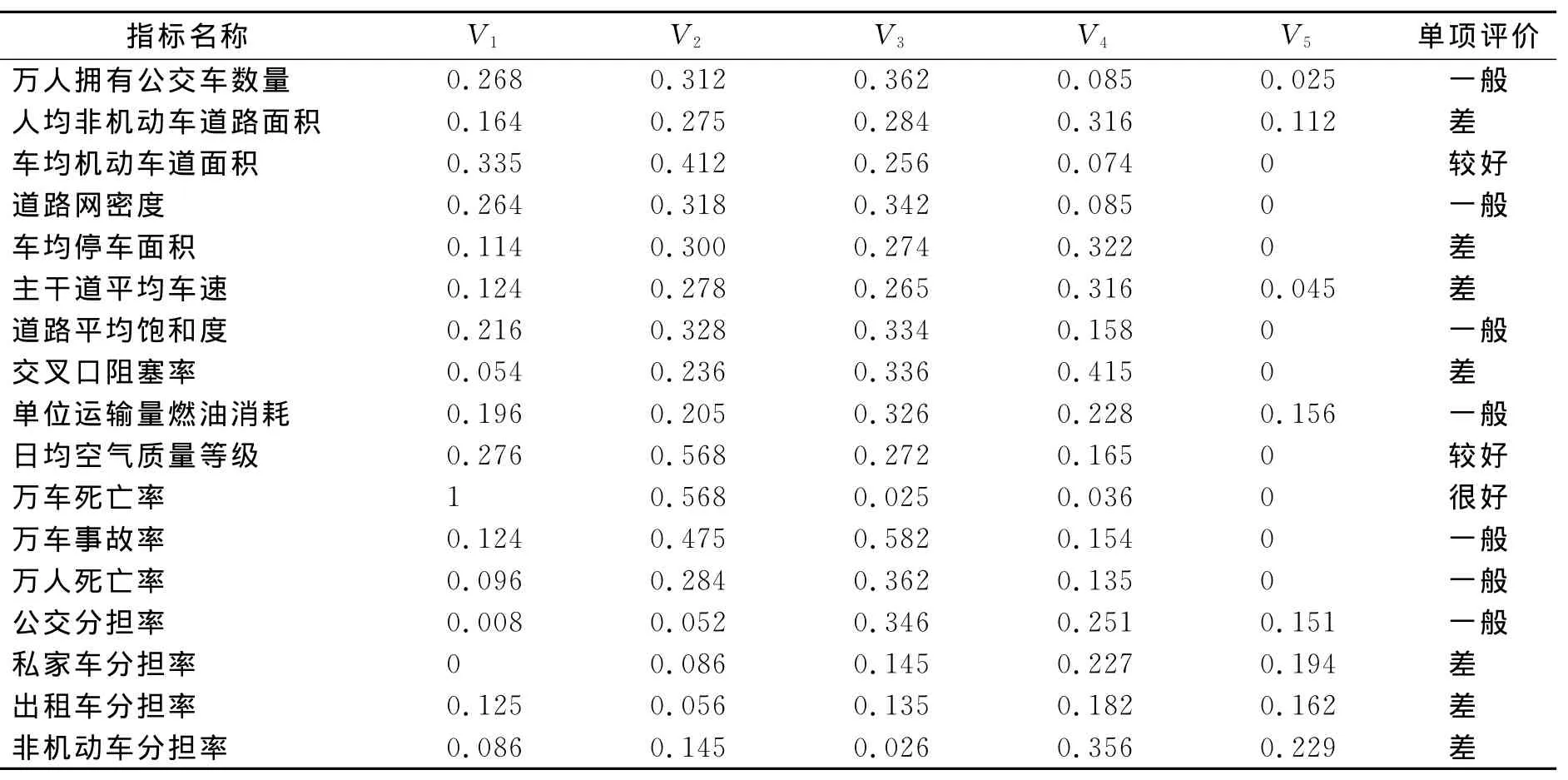
表4 武汉市城市交通综合评价体系二级指标评价结果

表5 武汉市城市交通综合评价体系一级指标评价结果

表6 武汉市城市交通综合评价结果

根据表6结果可知，用式（21）对评语结果进行定量化处理后，武汉市城市交通综合评价的最高得分为77．65，小于80；最低得分为68．49，介于65和70之间．故武汉市城市交通综合评价为“一般”和“差”之间，而更偏向于“一般”，结果符合武汉市城市交通现状．

由表5的评价结果可知，武汉市城市交通中交通发展状况较差、交通畅通状况差，应加大交通设施投资力度，加大交通管制力度，改善交通结构、交通环境和交通安全．

［1］傅新平，胡伶俐．基于物元分析法的综合交通系统服务水平评价［J］．武汉理工大学学报：交通科学与工程版，2007，31（4）：580－581．

［2］郭秀芝，陆化普．城市交通系统整体发展水平综合评价指标体系及方法［J］．交通标准，2003，120（8）：53－54．

［3］陆 建，王 炜．面向可持续发展的城市交通系统综合评价方法研究［J］．土木工程学报，2004，37（3）：101－102．

［4］Fu Xinping，Zou Min．Application of combination weighting method in contract risk＇s evaluation of third party logistics［J］．Journal of Southeast University：English Edition，2007，23：130－131．

［5］刘 虹，陈学武．公路建设项目社会经济环境影响评价方法研究［J］．交通信息与安全，2008，26（6）：92－93．

［6］吴晓平，汪 玉．舰船装备系统综合评估的理论与方法［M］．北京：科学出版社，2007．

［7］王新洲，史文中．模糊空间信息处理［M］．武汉：武汉大学出版社，2003．