教育测验中学生能力水平与测验项目难度的Rasch模型分析*——个体能力与题目难度之间的对应关系

● 张金勇 何妃霞

教育测验中学生能力水平与测验项目难度的Rasch模型分析*
——个体能力与题目难度之间的对应关系

● 张金勇 何妃霞

本文以2011年贵阳市第八中学第一次高三英语高考模拟考试为例，使用Rasch分析软件WINSTEPS对其进行分析，可以得出学生与学生、测验项目与项目以及学生与测验项目之间的关系。研究结果表明，该试题的内容覆盖了所有能力水平的学生，且能够较好地区分学生的能力水平。研究结果得出学生的能力水平略高于项目的难度水平，对样本群体的测验目标较明确；测验中间的项目难度水平接近；测验项目涵盖的内容不够；缺乏难度较大的项目。

Rasch模型；WINSTEPS；教育测验；难度；能力水平

科学测评学生学业成就对于改进学校教学质量、公平评价学生、促进学生发展和教师专业发展具有重要意义。而科学测评学生学业成绩，测验项目与测评目标、学生能力相吻合非常关键。测验项目的难度是测验项目质量的重要指标，不仅直接关系到测验的可靠性与准确度，而且还直接或间接地影响到学生的学习态度和学习行为。尽管考生的得分受到评分者的标准把握程度、项目特定等级的难度等因素的影响，但主要决定于考生的能力和测验项目的难度。因此，如何使测验项目与被测对象的能力水平一致，是教育测量与考试研究的重要课题。这里我们借助Rasch模型，运用实例在一个连续尺度上呈现教育测验的结果，分析教育测验质量，研究学生的能力水平和测验项目难度、学生与学生、测验项目与项目等之间的关系。本研究对试卷质量及考生能力分析具有一定的启示和借鉴。

一、研究的理论基础：Rasch模型

Rasch模型是丹麦数学家Georg Rasch（1960）提出的一种潜在特质模型，通过个体在题目上的表现来测量不可直接观察的、潜在的变量，分析测试分数之间的差异。它可以同时估计项目难度和个体能力，是包含考生能力和项目难度层面的双面模型。

近年来，国内外学者对Rasch模型的原理进行了较为深入的研究。这一模型以自然科学领域内的客观测量为标杆，为社会科学领域内的测量建立起一套客观标准，在教育和心理测量领域得到广泛的应用，多集中于在CET、教师评分等级、学生学业成就估计、学生学业成绩的分析等。如田清源（2006）认为Rasch模型对测验中主观评分的分析有重要影响，可以降低对学生成绩估计的测量误差[1]；何莲珍、张洁（2008）的研究结果显示Rasch模型在CET口语考试、分数等值等研究中有重要作用[2]；Michela Battauz，Ruggero Bellio，Enrico Gori（2008）认为通过结合 Rasch 模型和教师评分可以减少学生学业成就估计的误差[3]。但大多数的研究不够深入，在基础教育中的应用研究也比较缺乏，尤其是在项目难度与考生能力水平分析方面不足。

Rasch模型有四个最基本的假设：一是每个个体有其特定的能力；二是每个项目有一个难度；三是每个项目的难度可以呈现在同一标度上；四是可以计算任何特定观察分数反应概率数目之间的差异[4]。对于客观测量，Rasch模型有两个要求：一是对任何题目，能力高的个体应该比能力低的个体有更大可能作出正确回答；二是任何个体在容易题目上的表现应该始终好过在困难题目上的表现。[5]Rasch模型是一个理想化的数学模型，要求所收集的数据必须符合模型的先验要求，才能实现客观测量。如果数据与模型不拟合，就必须拒绝数据，而不是模型[6]。

依据上述观点，运用Rasch模型，可以估计测验项目之间、学生之间以及测验项目与学生之间的关系，可以在同一个图形中使用等距的单位来描述个体和项目的潜在特质[7]。Rasch模型通过原始分数来计算学生的能力和项目的难度，把学生能力和项目难度的测量单位转换为等距的logit。该模型中的能力参数与难度参数可以真正相互独立地估计出来，且学生总分和项目总分是能力参数与难度参数的充分估计值。因此，Rasch模型可以为学生和项目建立一个等距分数。另外，Rasch模型对分布在中间的项目和学生的估计要比分布在边缘的项目和学生更精确。Rasch模型通过学生对测验项目的反应来测量个体的能力水平和测验的难度水平。根据Rasch模型原理，学生答对特定项目的反应概率可以用个体能力与该题目难度的一个简单函数来表示，即其中，Pni是考生正确作答项目i的概率，（1-Pni）是考生答错项目i的概率，Bn是考生n的能力值，Di是项目i的难度。因此，个体能力和项目难度共同决定了个体对特定项目正确反应的概率。学生能力越高，对项目正确回答的概率越大。如果个体的能力等于项目的难度，那么正确回答的概率为0.5；如果个体的能力显著大于项目难度，那么正确回答的概率接近1；相反，如果个体的能力小于项目难度，那么正确回答的概率接近0[8]。

二、研究数据的选取与处理

本研究的样本学校学生是贵州省贵阳市第八中学高三学生。研究数据来源于贵州省贵阳市第八中学高三学生第一次英语高考模拟考试。数据总数为643个，剔除无效数据12个，有效数据个数为631，数据有效率高达98%。用社会科学统计软件包SPSS15.0对数据进行预处理，并用WINSTEPS3.38作Rasch分析。

三、研究结果与分析

（一）样本学校学生测验的经典理论分析

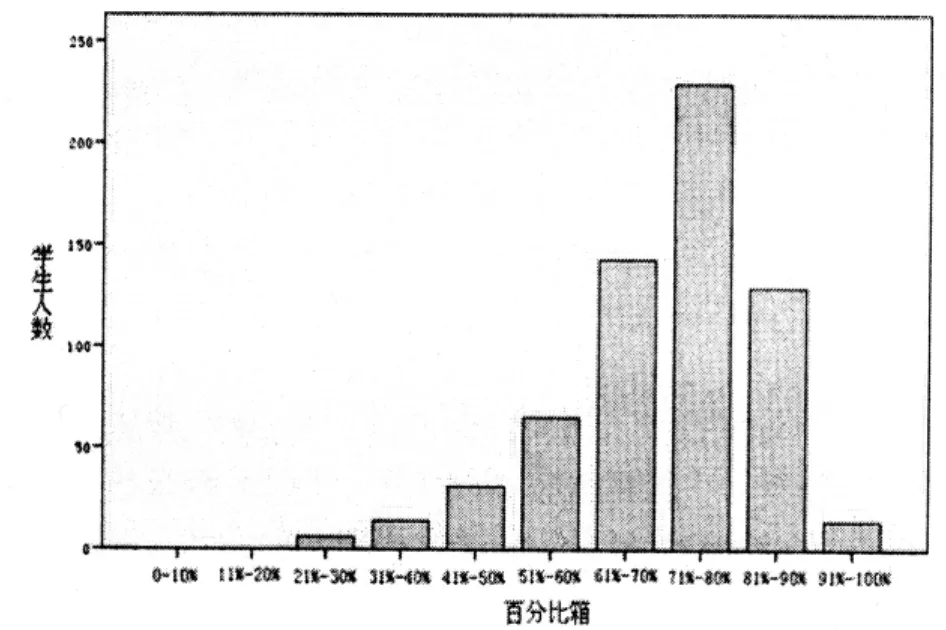
图1呈现了样本学校学生的分数分布情况。其中横坐标表示学生的得分率。图1表明，大部分学生处在高分端，对知识的掌握较好，学生成绩呈负偏态分布。

（二）样本学校学生测验的Rasch模型分析

1．测验项目的难度与学生能力水平整体近似正态分布，学生能力水平相对高于测验项目的难度水平。

图2中，横轴右边是模拟测验项目难度的分布，左边是学生能力水平的分布。图2清晰地呈现了测验项目难度和学生能力的分布形态，都近似于正态分布。同时，还可知，学生能力与测验项目之间的关系——横轴原点处表示个体正确回答题目的概率为50%，能力在原点以上的学生对原点以下的项目正确回答的概率大于50%。从图中可以看出学生的能力分布宽度大约为6.4个logit，项目难度的分布宽度约为5个logit，由此可以看出学生的能力水平相对高于测验项目的难度水平。也就是说，作为高考的模拟测验，其项目难度设计与学生的实际水平之间不太吻合，难度偏低，这样就会使测验的区分度降低。

2．测验项目难度分布不均匀，试题便易，区分度较低

横轴上部分清晰地呈现了65个项目之间的关系，项目间的距离代表项目之间的难易程度差异，越靠近顶端的项目难度越大，越靠近下端难度越小。同时项目之间的距离越近，说明项目的难度水平越接近，对学生的能力水平进行估计时误差也较大。图的左边呈现学生能力的分布情况，越靠近图的顶端，学生能力越强，对项目的答对率越高。顶端的项目适合那些能力水平较高的学生，下端的项目适合能力水平较低的学生。从图2可以看出，模拟测验中较难的题目偏少，容易的试题偏多，试题之间的难度水平差距不大，难度相近的试题分布较为集中，这样就不能对高低不同能力水平的学生做出很好的区分，高考模拟测验的有效性就不太高。

3．学生能力水平差别较大，能力水平与部分测验项目呈负相关，测验项目与测验目标基本一致

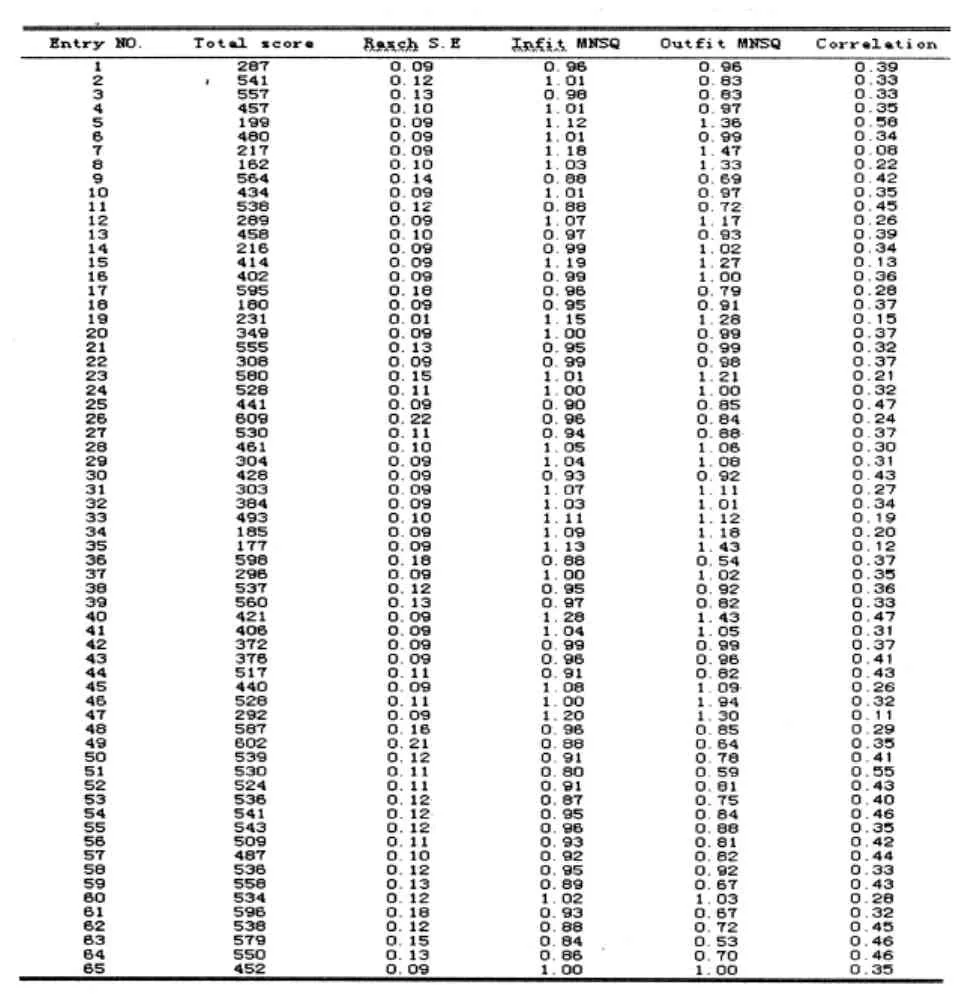
表1 样本学校高三学生RASCH模型项目信息表

表1中难度项目和学生能力测量的Rasch标准误（第三列Rasch S．E）代表估计的不确定性。表中第二列代表学生在65道题目上答对的学生人数。Outfit MNSQ表示标准残差的均方。一个项目的Outfit MNSQ值越大，表明个体能力水平和项目难度水平差异显著时，能力水平高的学生答错了简单项目，能力水平低的学生正确回答了较难的项目，学生能力水平差别也较大，能力水平与回答题目呈现负相关。例如项目23是较容易的项目，但Outfit MNSQ值为1.21，表明一些高能力水平的学生未能对该项目作出正确回答；项目8是较难的项目，Outfit MNSQ值为1.33，说明一些低能力水平的学生正确回答了该项目。这两种情况的试题都是测验设计时不想出现的结果，教师需要对这样的试题进行修改。Infit MNSQ表示加权后的残差均方。对于一个特定项目，如果Infit MNSQ值较大，说明与项目难度水平接近的学生作答的方式与模型不一致，如项目7和项目35，但总体基本符合样本学校学生的能力水平。从表1第六列可以看出，所有测验项目的相关系数都是正向的，表明测验项目与测验目标基本一致，测量相同的潜在结构。

根据 Rasch模型原理，Infit MNSQ和 Outfit MNSQ的理想值为1，但在实际项目分析中，Infit MNSQ和Outfit MNSQ值在0.5-1.5之间即可认为与模型拟合。此外，Rasch标准误不超过±0.75也在可接受的范围。从表1中的结果可以看出，测验分数的Rasch分析表明，Rasch标准误、Infit MNSQ以及Outfit MNSQ值均在可接受的范围内，即可以对测验项目和学生能力做出较全面、客观的评价。

4．测验项目难度接近，顺序不清晰，对学生能力的估计不够精确

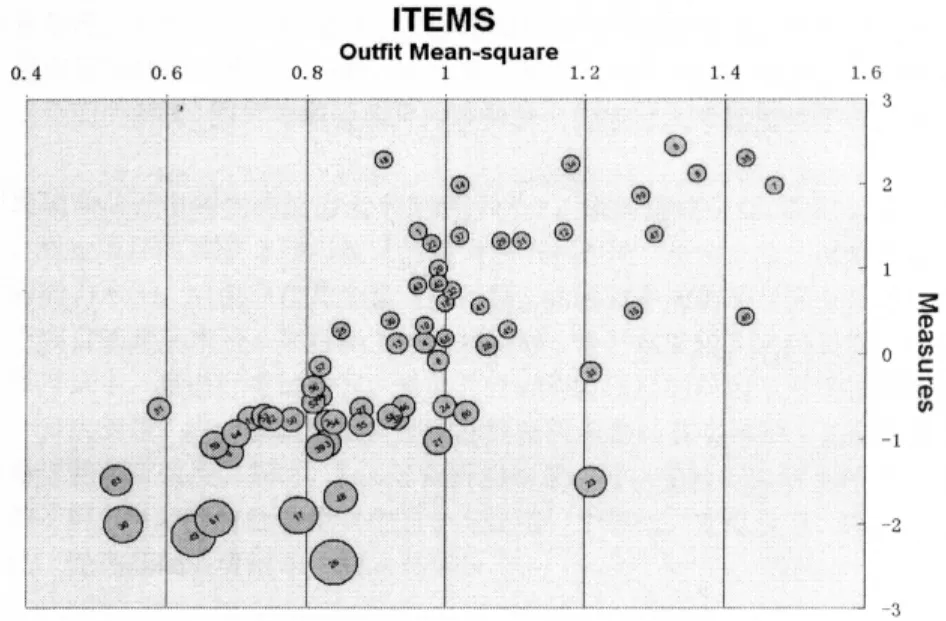
图3中用气泡代表每个项目，气泡的大小代表Rasch标准误的比例。气泡的比例越小，说明该测验对学生能力水平的估计越精确；比例越大，对学生能力水平估计的误差就越大。理想状态下，测验项目应靠近气泡图的中轴线。从图中可以看出，许多气泡重合了，表明项目的难度非常接近，从而导致项目顺序不清晰。项目越简单，学生的通过率越高，对学生能力的估计就不精确，代表项目的气泡就越大，就不能对学生能力做出很好的估计和区分，如项目36、26、49等。位于气泡图左边的项目，如25和51，两个项目的Infit MNSQ和Outfit MNSQ值都小于1，说明与模型拟合比预期好，学生在测验项目上的答对率高。位于气泡图右边的项目，如 7、15、19、40 和 47，表明除了受到项目难度和学生能力水平的影响外，还受到较多外在因素的影响。图中8、18、34和35都是很难的项目，它们的Outfit小于1.3，这可能是由于低能力的学生猜测正确造成的。

四、研究结论与讨论

理想的测验应该是测验项目集中在学生能力分布周围。通过Rasch模型分析，本测验的项目难度水平与学生能力水平基本相当，但个体的能力水平略高于项目的难度水平。从表1中可以看出大多数测验项目与测验的目标接近，这说明大多数项目是有效的，该测验能够较好的测出预测的知识和技能。同分布在两端的项目和学生相比，该测验对分布在测验中部项目难度和中等能力水平的学生做出的估计更精确。例如项目26，根据表1中的数据，它的Rasch分析误差最大，项目26的参数结果不如其他项目的估计结果精确，对学生的测验目标也不够明确。因此，根据分析结果，在设计测验或建立题库时，像26这样的项目需要进一步的修改和探讨，以便使其更具有针对性和有效性。

Maja Planinic,Lana Lvanjek,Ana Susac（2010）在一项研究中发现，针对测验的宽度不足以覆盖样本学生的能力范围，测验中部有许多项目的距离接近，测验两端没有充足的项目，这时需要在测验的两端增加项目来提高测验的效度。[9]依据这一研究结果，该测验对于该样本学生来说较简单，需要在测验的两端增加一些项目，比如像8、18、35这样的项目，删除一些中间的项目，以便能够更加精确的估计学生的能力。同时，也需要增加测验的总体难度来提高测验的上限。另外，该测验中有些项目是重叠的，测量的内容是相同的，这就需要对试卷结构进行调整。调整时要根据学生能力分布的大致情况和测验项目难度的分布情况，以及测验目标，删减或合并相同内容的题目，增加新内容，使测验充分体现测验目标，提高的内容效度。另外，可以针对学生实际掌握和运用知识的情况，进行教育教学调整，使教学更能适应学生的实际水平。因此，运用Rasch模型对测验进行分析，不仅能够对测验分数做出比较全面的解释，同时对测验项目内容和学生的能力水平都提供了一个合理的评价依据。

客观准确地估计出考生的能力水平是测评活动追求的最终目标，而测验要达到理想的信度和效度，测验项目的难度必须与被试的能力水平相匹配。总的来看，该测验项目基本符合样本学生的能力水平，但也存在几个显著的问题，如测验中间的项目区分度不明显、学生能力水平高于项目的难度水平、项目涵盖的内容不够、缺乏难度较大的项目等。这就要求高中教师在模拟考试中，要进行考试研究，侧重于分析测验项目的问题以及考试的实际能力，而不是侧重于多次测量；进一步研究如何使试题既反映考生的真实水平，又反映测量目标，保证测验的科学性和有效性。同时，Rasch分析的结果，可以使教师对学生的知识掌握水平有一个清晰的了解，为老师的教学和学生的学习提供一个导向，使得学习、教学和测验的编制更有针对性，促进基础教育改革的深入发展。

[1]田清源．主观评分中多面Rasch模型的应用[J]．心理学探新，2006,26(1)：70-73．

[2]何莲珍，张洁．多层面Rasch模型下大学英语四、六级口语考试(CET-SET)信度研究[J]．现代外语，2008：31(4)：388-437．

[3]Michela Battauz,Reggero Bellio,Enrico Gori.Reducing Measurement Error in Student Achievement Estimation[J].PSYCHOMETRIKA,2008，(2):289-234.

[4]Trevor G.Bond,ChristineM.Fox.Applying the Rasch Model:Fundamental Measurement in the Human Sciences[M].Lawrence Erlbaum Associates,2007.26.

[5]Wright,B.D.,&Stone,M.H.（1979）.Best test design Chicago:MESA Press.

[6]晏子.心理科学领域内的客观测量——Rasch模型之特点及发展趋势[J]．心理科学进展，2010，(18)：1298-1305.

[7JDouglas H.Clements,Julie H.Sarama,Xiufeng H.Liu.Development of a measure of early mathematics achievement using the Rasch model:the Research-Based Early Maths Assessment[J].Educational Psychology,2008，(28):457-482.

[8][9]Maja Planinic,Lana Ivanjek,Ana Susac.Rasch modelbased analysis of the Force Concept Inventory[J].Phisics Education Research.2010，(6).

张金勇/贵州师范学院教育科学学院讲师 何妃霞/贵州师范大学教育科学学院硕士研究生

*本研究为贵州省高等学校教学质量与教学改革工程重点项目“基于PBL理论改进心理教育测量教学改革研究”（项目批准号：黔高教发[2011]28-1）、贵州师范大学精品课程“心理测量”建设项目阶段性成果。

（责任编辑：曾庆伟）