台风下香港K11大楼风振响应实测及分析

林 巍，黄铭枫，郭中秀，楼文娟

1)浙江大学结构工程研究所，杭州310058;2)香港科技大学土木与环境工程系，香港

近年来，高层建筑朝越来越高、越来越柔的方向发展.这些建筑自振频率较小，在强风作用下动力响应较大，在台风下尤为明显.李秋胜等［1］对台北101大楼进行了风振实测分析研究.吕西林等［2］对上海几幢超高层建筑的振动特性进行了实测.原型实测可以验证现有结构风振分析技术，并推动相关风工程理论的发展.随着越来越多风敏感高层建筑在各地的兴建，风振舒适度性能设计研究及其相应的设计标准和评价方法已成为风工程热点问题之一［3］.利用风振实测数据可方便解决高楼的风振舒适度评价问题.本研究选取香港维多利亚港附近K11超高层建筑在台风作用下的实测加速度数据进行分析，并对其进行居住舒适度评价，旨在为高层建筑的抗风性能设计提供依据.

1 研究背景

K11大楼位于香港维多利亚港附近，主楼68层，结构总高度约270 m.主楼承重系统以井字形巨型剪力墙构架为主，每隔20层设置巨型桁架转换层.剪力墙沿结构短轴向(y向)布置.主楼结构平面为长方形，长58 m，宽22 m，结构高宽比大于10，超过现行结构规范规定的标准，结构较柔，属于对风敏感建筑.大楼顶层安装有GPS监测系统和加速度传感器，从而可获得丰富、实时的结构风致振动响应数据，以评估建筑在强风强震下的舒适性、安全性和可靠性.顶层平面GPS和加速度传感器测点布置如图1，包括位于角部的测点1和位于大楼中心位置的测点2.其中GPS主要用来测量建筑物的风致位移，通常包括共振、背景和静力分量，加速度传感器用于测量加速度响应.限于篇幅，本研究只讨论由加速度传感器所测得的风致加速度响应时程数据.加速度传感器的采样频率为20 Hz.

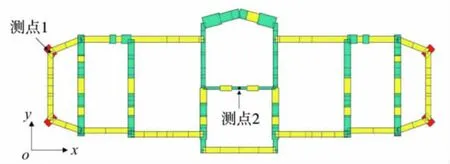
图1 结构平面图Fig.1 The plan view

2008-08-04 清晨北冕 (Kammuri)在香港东南580 km的南海东北部形成热带低气压，并向西北偏西移动，翌日早上增强为热带风暴.8月6日清晨北冕增强为强烈热带风暴并向西北移动，早上在香港西南偏南约130 km处掠过，当日下午转向西移动.在8月6日10∶00左右最接近香港，位置在香港西南偏南约130 km.其移动路径如图2.香港气象台在横澜岛上海拔90 m高度处的风速仪测得最大每小时平均风速为26.7 m/s，最大3 s阵风风速为38.9 m/s.横澜岛附近录得最低气压为98.75 kPa.香港天文台为此于8月6日5∶40发出8号东北烈风或暴风信号，当时北冕位于香港以南约180 km.6日8∶40香港天文台改发8号东南烈风或暴风信号.

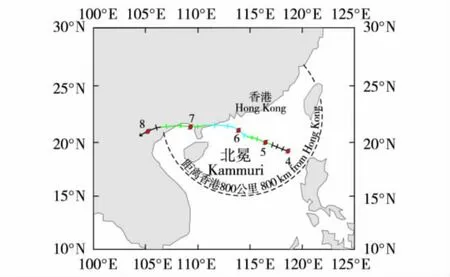
图2 2008年台风“北冕”路径图Fig.2 Track of Kammuri in 2008

2 实测风振数据分析

2.1 结构风振响应概率分布特性

结构顶层加速度是评价高层建筑安全性和舒适度的重要指标，研究实测加速度响应的概率分布特性具有重要意义.对随机过程的概率统计常用三阶和四阶统计量偏度及峰度来描述.偏度反映随机信号概率分布曲线的对称性，峰度反映随机信号概率分布曲线的陡峭程度.高斯信号的偏度值为零，峰度值为3.若实测加速度的峰度大于3，则表明其概率分布较正态分布曲线陡峭，小于3则表明较正态分布曲线平坦.

表1给出K11楼层顶部两个测点实测加速度数据的前四阶矩统计量，其中，台风实测加速度用milli-g表示.对各测点实测加速度值正则化，绘制概率密度图如图3.由表1和图3可知，实测加速度的偏度值接近0，峰度值接近3，其概率密度分布曲线与标准正态分布基本符合.但加速度数据也说明了轻微的非高斯特性，如中心测点2沿x方向加速度过程的峰度值小于3，图3中概率密度分布曲线中段表现出比高斯分布更为平坦的特点.表1和图3的结果还表明，K11大楼和其他大多数高层建筑一样，其风致加速度响应的分布基本符合高斯分布.但风致响应服从高斯分布的结论是有条件的，即高层建筑在台风作用下应仍处于线弹性工作阶段.若因某种原因，如经受地震作用后的损伤累积和刚度退化等，高层建筑某些构件会处于弹塑性工作状态，这样其结构行为就不一定仍是线性的，响应分布也就不一定呈高斯分布.由于非线性系统的风振分析和风洞试验理论还不十分完善［4］，利用实测的加速度数据分析其分布特征就具有更为重要的意义.

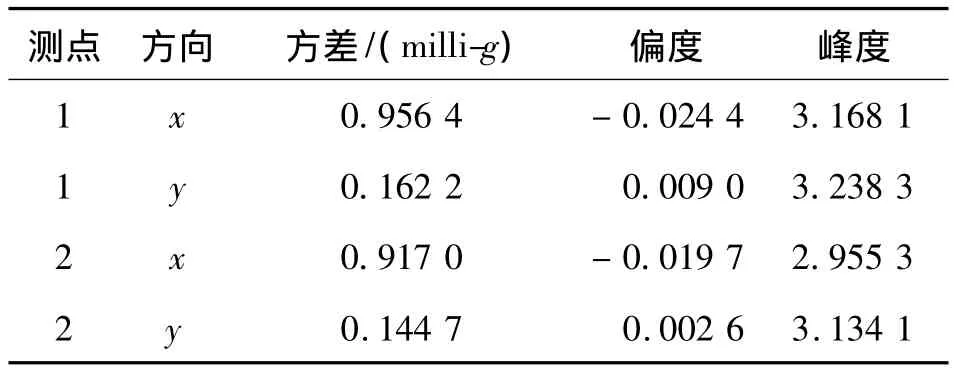
表1 实测加速度的各阶统计量Table 1 The order statistics of measured accelerations

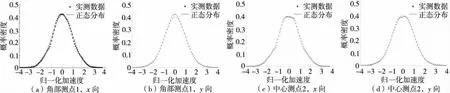
图3 K11大楼顶层测点加速度概率密度分布Fig.3 Probability density charts of acceleration data

2.2 结构自振频率

通过对测点实测加速度响应信号进行功率谱分析，得到结构的模态参数.图4给出测点1和2沿x与y两个方向上的加速度功率谱.由图4可知，功率谱的峰值明显，从中可方便识别结构的自振频率.所识别的结构频率值直接标注在各谱形图中.由于x方向加速度响应比y向大，结构扭转模态可以通过比较角部测点和中心测点x方向加速度的谱形图来识别.角部测点和中心测点x向加速度谱均在0.205 Hz和0.439 Hz各有一个尖峰，可见这两个频率值代表了结构沿x向的一阶和二阶平动振型频率.而角部测点x向加速度谱比中心测点x向谱在0.342 Hz处多了一个明显的峰值，这个峰值是由于结构的扭转在角部产生的平动分量，从而可以判定0.342 Hz为结构的扭转振型频率.

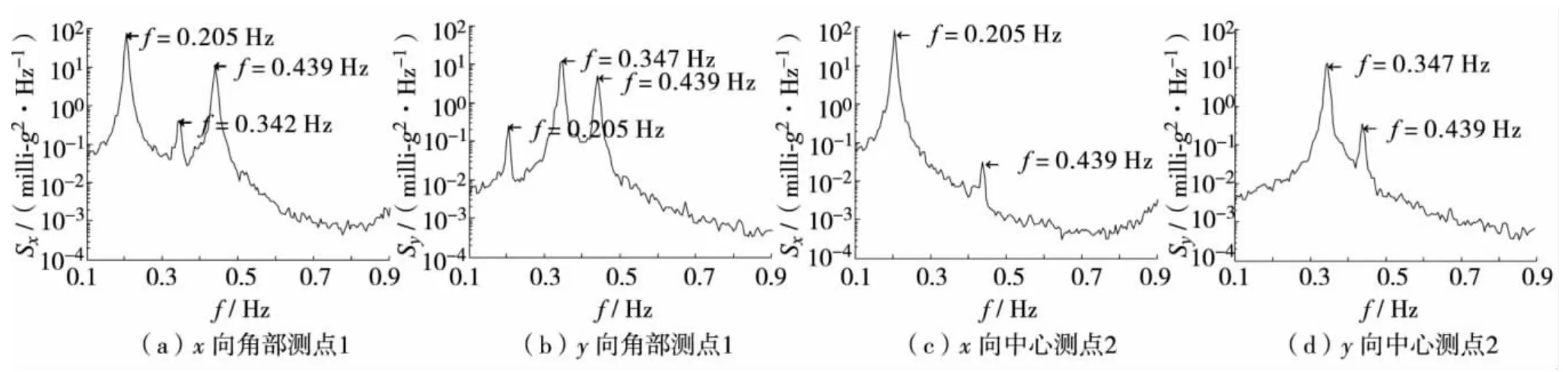
图4 实测加速度功率谱Fig.4 The power spectral density of measured acceleration

为进行对比分析，根据结构施工图采用SAP2000进行三维有限元建模，计算其自振频率.梁柱及桁架杆件用FRAME单元描述，剪力墙及楼板用SHELL单元描述.

虽然结构平面为长方形，但因剪力墙沿y向布置，使y向结构较刚.由功率谱分析法识别的结构自振频率和由有限元模型计算所得的结果列于表2.由表2可知，有限元计算结果较实测结果偏小，这与有限元模型计算时未考虑非结构部分的刚度贡献有关.另外模型误差 (包括材料物理特性和截面特性的偏差、边界条件的不确定性等)及实地测量误差也导致了有限元分析与实测结果之间的较大偏差.为便于比较，表2列出了根据各经验公式得出的高层结构频率预测值.与有限元模型相比，这些经验公式给出了和实际测量值更为接近的频率预测值.为使有限元模型能更精确预测该大楼在将来台风等极端气候条件下的动力响应，可以通过结构动力模型修正方法对该楼的有限元模型进行更新，使其动力特性符合实际现场测量结果［5］.限于篇幅，涉及动力模型修正部分不在本文讨论.

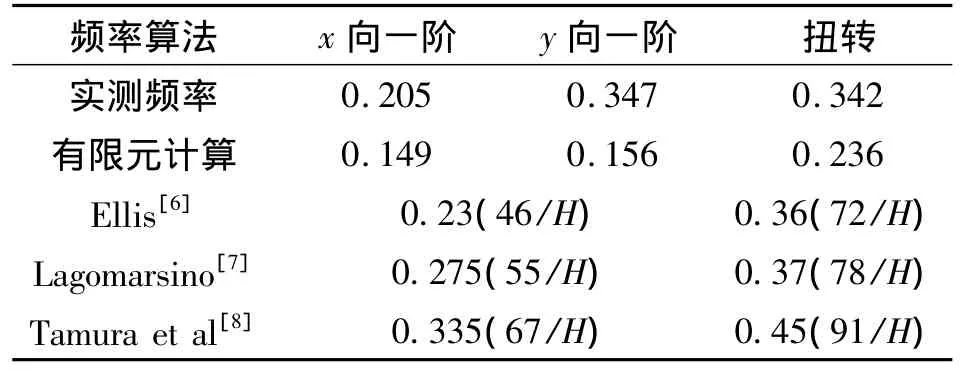
表2 结构自振频率Table 2 Natural frequency of the structure 单位:Hz

2.3 加速度响应峰值因子计算

其中，xe为峰值因子;平均值和根方差δx可以根据时程信号得到.对于峰值因子的取值，往往是在假设随机过程符合高斯概率分布的基础上进行推算.在 GB50009-2001［9］中，基于高斯分布假定，建议峰值因子取2.5，则可达到99.38%的保证率.通过根方差和峰值因子确定的峰值加速度通常可以用来评价高层建筑的居住舒适度.

基于零穿越理论，由 Davenport［10］发展而来的标准高斯过程的峰值因子法，可得峰值因子为

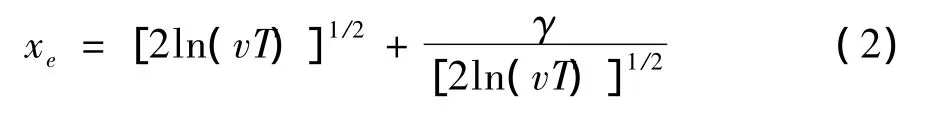
其中，γ=0.577 2(欧拉常数);v为高斯过程的零值穿越率，可以估计为

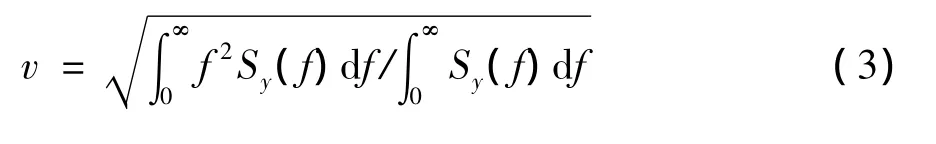
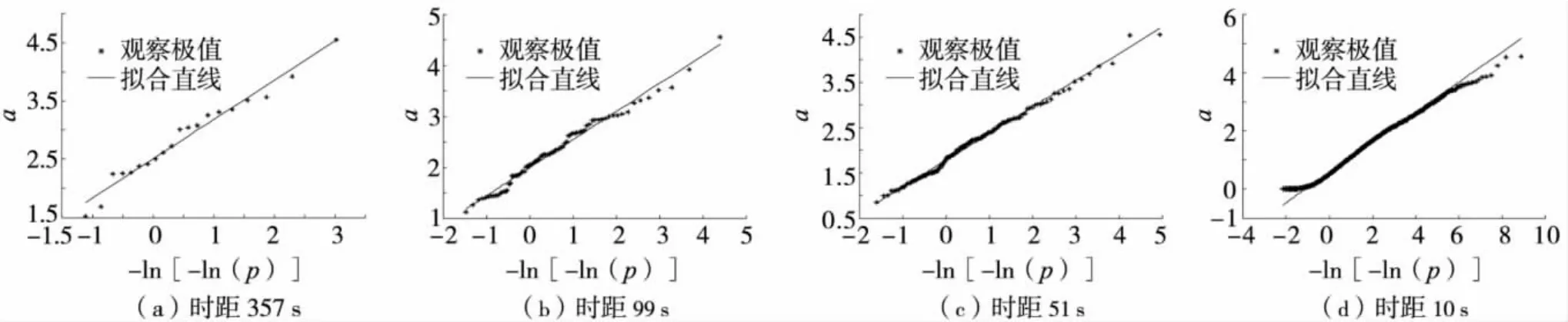
图5 角部测点x方向加速度的Gumbel图Fig.5 Gumbel diagram of x-direction acceleration at corner measurement point

其中，f为频率;Sy(n)为功率谱密度函数.

基于经典极值理论的Gumbel法认为，高斯过程的极值服从极值Ⅰ型分布 (Gumbel分布).其概率分布函数为

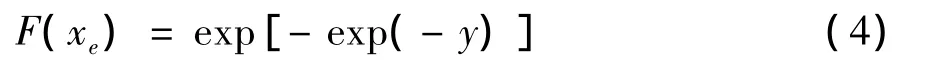
其中，可引入简化变量

参数u和1/b分别称为模和散度.由于估计极值的需要，式 (4)和 (5)可变为

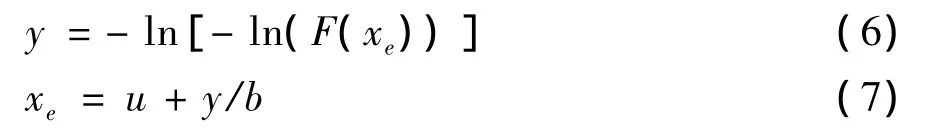
平均极值

标准Gumbel法通常需要大量样本才能得到可靠结果.为此，本研究采用改进的 Gumbel法［11］，通过n个短时距下的观察极值，得到目标时距下极值分布的两个参数u和b，从而计算出目标时距下的峰值因子.

设目标时距为t1的数据划分为若干段时距为t2的数据(t1≥t2)，则划分段数n=t1/t2.记时距t1下的极值小于x的概率为F(T=t1)，时距t2下的极值小于x的概率为F(T=t2)，由极值间的独立性有

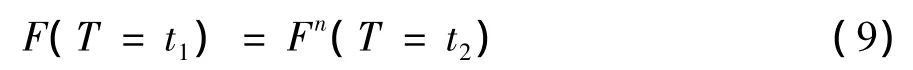
将式 (4)和式 (5)代入式 (9)，简化可得

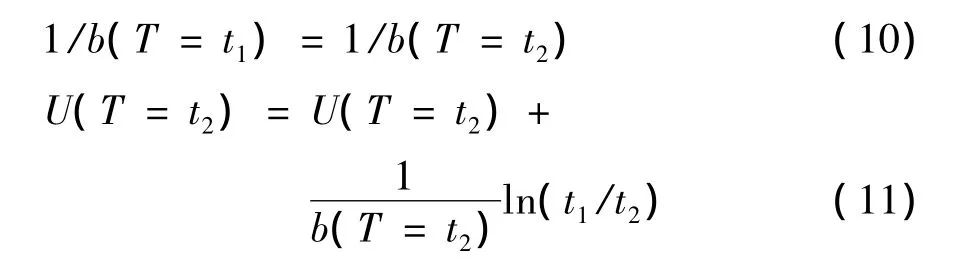
对各测点已标准化的加速度时程a，按实际观察时距357 s、199 s、99 s、51 s、22 s和10 s进行划分，分别绘制Gumbel图，观察可知各测点的观察极值能较好地服从极值Ⅰ型分布.图5给出角部测点1处x方向加速度数据在各典型时距分段下的Gumbel图.极值分布的u和b可通过Gumbel图中拟合直线的斜率和截距确定.由图5可见，51 s为最佳观察时距.当分段时距较大(357 s)时，由于观察极值的数目较少，数据较为离散;当分段时距很小 (10 s)时，数据间隔较小，数据间的相关性增强，在Gumbel图中的尾部和端部与拟合直线有较大的偏差.

峰值因子法与改进的Gumbel法计算结果有较好的可比性，两者结果见表3.最大误差7.04%发生在中心测点2沿x方向的加速度.这是由于测点2沿x方向所测加速度数据的峰度值小于3(见表1)，说明该加速度过程具有比高斯分布更窄的尾部，及较小的峰值因子，所以传统峰值因子法高估了7.04%.与峰值因子法相比，改进Gumbel法也适用于具有非高斯特性的随机过程.

表3 各测点的峰值因子Table 3 Peak factor of the measuring point

3 台风下K11大楼居住舒适度评价

到目前为止，国际上广泛采用建筑物的风致加速度响应来评价高层建筑居住舒适度性能，但还没有统一的风振舒适度标准.在各国和国际标准化组织 (ISO)推荐的风振舒适度标准中，用到的加速度响应指标包括均方根值、峰值模态加速度和峰值合成加速度等.其中均方根和峰值模态加速度通常用于和频率相关的舒适度性能标准.如ISO-6897标准［12］规定，5年重现期的风速条件下10 min振动时距的均方根加速度指标应满足

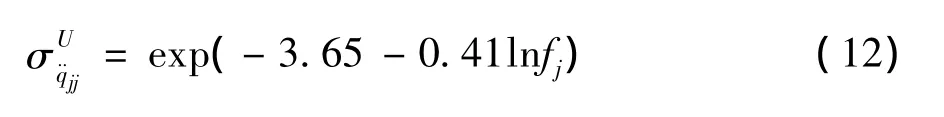
日本规程AIJ-GEH-2004［13］也采纳了与频率相关的具有1年重现期的峰值模态加速度指标，评价高层建筑的居住舒适度.根据日本规程，式 (13)给出的1年重现期峰值加速度限值对应于大楼90%的居住人员将会感知风振，

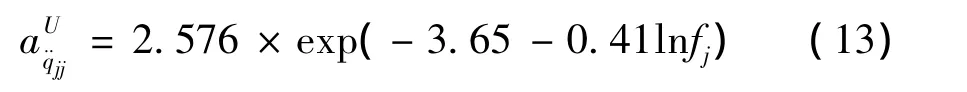
K11大楼具有1年重现期的峰值模态加速度指标，可利用实测加速度方差0.956 4 milli-g和由改进Gumbel法估计的峰值因子3.568及重现期转换系数0.95得到，为3.24 milli-g，满足要求.

在10年重现期偶遇风灾下，与频率无关的峰值加速度指标也被不少国家和地区的相关风荷载规范所采纳和推荐，包括中国大陆和香港的规范［14-16］等.参考中国《高层民用建筑钢结构技术规程》［14］和《高层建筑混凝土结构技术规程》［15］，公共建筑的峰值加速度限值分别为28和25 milli-g.该楼在台风北冕下的期望峰值加速度为0.956 4×3.568=3.41 milli-g，相应的在10年重现期台风下的峰值加速度为5.57 milli-g，亦满足要求.为便于比较，3种不同标准下该大楼居住舒适度评价结果均列于表4.由表可知，3种不同标准下加速度限值与加速度指标的比都在4左右，说明这些标准虽然表达形式不同，但本质上对风振舒适度的要求一致.

表4 台风下K11大楼居住舒适度评价Table 4 Occupant comfort assessment

结 语

综上研究可知:① 在台风作用下，结构的风振加速度响应基本符合高斯分布，但也表现出轻微的非高斯特性;②通过加速度时程的功率谱分析，得到了结构的前几阶自振频率;并与有限元计算结果和相关经验公式预测值进行了对比;③分别通过基于零穿越理论的峰值因子法和基于经典极值理论的改进Gumbel法计算了风振加速度响应的峰值因子，两种方法所得结果基本一致，规范取值偏低，改进Gumbel法也适用于具有非高斯特性的随机过程;④参考国内外各种高楼居住舒适度评价标准，利用实测的风致加速度方差和估计所得的期望峰值因子，对K11大楼进行了全面的居住舒适度评价，为超高层建筑的舒适度设计提供了依据和方法，结果表明大楼的居住舒适度在类似的台风作用下可满足各相关规范和标准.

/References:

［1］ LI Qiu-sheng，ZHI Lun-hai，DUAN Yong-ding，et al.Full-scale measurements and analysis of wind-induced response of Taipei 101 Tower［J］.Journal of Building Structures，2010，31(3):24-31.(in Chinese)李秋胜，郅伦海，段永定，等.台北101大楼风致响应实测及分析［J］.建筑结构学报，2010，31(3):24-31.

［2］ LU Xi-lin，SHI Wei-xing，SHEN Jian-hao，et al.Vibration properties of several tall buildings in Shanghai［J］.Building Science，2001，17(2):36-39.(in Chinese)吕西林，施卫星，沈剑昊，等.上海几幢超高层建筑振动特性实测［J］.建筑科学，2001，17(2):36-39.

［3］ Tamura Y，Kawana S，Nakamura J，et al.Evaluation perception of wind-induced vibration in buildings［J］.Proceedings of the Institution of Civil Engineers:Structures＆Buildings，2006，159:283-293.

［4］ HUANG Zhong-wei，YANG Xiao-ling，YU Ping-jing.Similarity analysis of structural wind motion under complex damp［J］.Journal of Shenzhen University Science and Engineering，1999，16(4):1-3.(in Chinese)黄中伟，杨小玲，遇平静.复杂阻尼作用下结构风振的相似性分析［J］.深圳大学学报理工版，1999，16(4):1-3.

［5］ ZHU Hong-ping，XU Bin，HUANG Yu-ying.Comparison and evaluation of analytical approaches to structural dynamic model correction［J］.Advances in Mechanics，2010，32(4):513-525.(in Chinese)朱宏平，徐 斌，黄玉盈.结构动力模型修正方法的比较研究及评估［J］.力学进展，2010，32(4):513-525.

［6］ Ellis B R.An assessment of the accuracy of predicting the fundamental natural frequencies of buildings and the implications concerning the dynamic analysis of structures［J］.Proc Inst Civ Eng，1980，69(2):763-776.

［7］ Lagomarsino S.Forecast models for damping and vibration periods of buildings［J］.Journal of Wind Engineering and Industrial Aerodynamics，1993，48:221-239.

［8］ Tamura Y，Suda K，Sasaki A.Damping in buildings for wind resistant design［C］//Chenju，Proceedings of the International Symposium on Wind and Structures.Seoul:Techno-press，2000:115-130.

［9］ GB50009-2001.Code of loads on building structures［S］.(in Chinese)GB50009-2001.建筑结构荷载规范［S］.

［10］ Davenport A G.Note on he distribution of the largest value of a random function with application to gust loading［J］.Proceedings，Institution of Civil Engineering，1964，28:187-196.

［11］ Quan Y，Gu M，Tamura Y，et al.An extreme-value estimating method of non-Gaussian wind pressure［C］//Cheng Chii-Ming，The Seventh Asia-Pacific Conference on Wind Engineering. Taipei:Techno-press，2009:723-726.

［12］ ISO 6897.Guidelines for the evaluation of the response of occupants of fixed structures，especially buildings and offshore structures，to low-frequency horizontal motion［S］.(in Chinese)ISO 6897.建筑物低频水平振动舒适度评价规程［S］.

［13］ AIJ-GEH-2004.Guidelines for the evaluation of habitability to building vibration［S］.(in Chinese)AIJ-GEH-2004.建筑振动可居住性评价规程［S］.

［14］ JGJ 99-98.Guidelines for steel structural design of tall buildings［S］.(in Chinese)JGJ 99-98.高层民用建筑钢结构技术规程［S］.

［15］ JGJ 3-2002.Guidelines for concrete structural design of tall buildings［S］.(in Chinese)JGJ 3-2002.高层建筑混凝土结构技术规程［S］.

［16］ Hong Kong Code of Practice.Code of practice for structural use of concrete［S］.