异形柱框架结构优化

朱杰江，袁 涛，王 坚

(1.上海大学 土木工程系，上海 20072;2.上海临港新城投资建设有限公司,上海 201306)

与矩形柱为主的传统框架结构相比，以异形柱为柱子截面的框架体系能使柱在转角处不外露，从而使房屋室内空间平整、布置灵活，所以越来越多的多层住宅开始采用异形柱的框架结构体系,对异形柱框架结构的优化必将带来巨大的经济效益.

在异形柱正截面承载力计算[1]方面，本研究采用的是数值积分法[2]来编制程序.在程序设计中，采用试算的办法，对截面进行了单元划分，得出了一个与外力平衡的应力状态，从而得到中和轴的位置和较满意的计算结果.文献[2]中“有效优化设计变量”的概念，探索对参数变量较多且普遍存在偏心的异形柱框架结构的优化问题进行了研究并编制了相关的程序，将梁的截面高度与宽度、异形柱的各项截面尺寸参数及楼层的混凝土强度等级都作为本研究的优化变量嵌入到了各级优化过程中.所有的变量都为离散变量，通过多级优化方法，即以结构楼层为基本单位的优化方法，使最终得到的结构优化解更符合实际工程的设计习惯，具有较大的工程意义.

1 异形柱正截面计算

1.1 数值积分法计算原理

数值积分方法是JGJ 149—2006《混凝土异形柱结构技术规范》[3]推荐使用的计算方法.该方法先将柱截面沿整体x轴和y轴划分成有限多个等尺寸或不等尺寸的混凝土方格单元或钢筋圆形单元，近似地取单元内的应变和应力为均匀分布，并假定各单元的合力点在其单元形心，合力大小为单元应力与单元面积的乘积.当截面的最大压应变点处的混凝土达到极限压应变时，由截面的中和轴方程及钢筋和混凝土的本构关系可得到每个单元的应变和应力.然后，对各单元的应力叠加即得截面的抵抗力.截面的轴力、弯矩和基本未知量之间的方程的求解需要利用计算机反复迭代运算来实现.

1.2 基本假定

(1)柱平均应变沿截面高度的分布规律，自加载开始直至破坏基本符合平截面假定，因而平均应变的平截面假定在T形、L形和十字形截面双向压弯柱中仍然适用；

(3)小方格(钢筋)单元内的应力和应变均匀分布，其合力点为小方格(钢筋)的形心；

(4)钢筋的应力—应变曲线采用斜直线加平直线的理想弹塑性模型，纵向受拉钢筋的极限拉应变取为0.01 ；

(5)混凝土受压应力—应变关系曲线、极限压应变可按现行国家标准GB 50010—2010《混凝土结构设计规范》[4]第6.2.1条的规定采用.

1.3 基本计算公式

1.3.1 中和轴方程

当异形柱截面在坐标系的第一象限、混凝土极限压应变值在坐标原点时，截面中和轴方程如下：

(1)

式(1)中，θ为中和轴法线方向与坐标轴x正向的夹角，以逆时针为正,R为坐标原点O到中和轴距离.

1.3.2 任意点的应变[5-6]

将柱截面划分为有限个混凝土单元和钢筋单元，近似取单元内的应变和应力为均匀分布，合力点在单元形心处；初步选定中和轴法线角度θ和坐标原点O到中和轴距离R，根据平截面假定即可求得截面上各钢筋及混凝土单元形心至中和轴的距离，进而求得截面上各钢筋及混凝土单元的应变:

一方面是劳动力素质技能偏低。陇西县农村劳动力素质和劳动技能均偏低，80%以上的务工人员均为初中文化，从事的工种仅局限于各种粗重的体力劳动和机械性劳动，与当前劳动力市场由体力型向专业型、技能型转变的要求很不适应，是制约陇西县劳动力外出务工的主要瓶颈，是农村劳动力转移就业的内在制约因素。另一方面务工人员工资水平较低、工作时间长。福州市各大企业的工资普遍较低，绝大多数劳务人员的月工资在2 500～3 000元左右，而劳动生产工作时间都在10～11 h（除3班制外）。

(2)

式(2)中，ε为任意点应变，压为正、拉为负,εcu为混凝土极限压应变值.

1.3.3 截面承载力公式

有了任一点的应变，就可以根据基本假定中钢筋及混凝土的应力—应变关系，求出钢筋及混凝土的应力σsj与σci，然后用JGJ 149—2006《混凝土异形柱结构技术规范》中公式5.1.2求出截面的承载力.

1.4 计算框图(见图1)

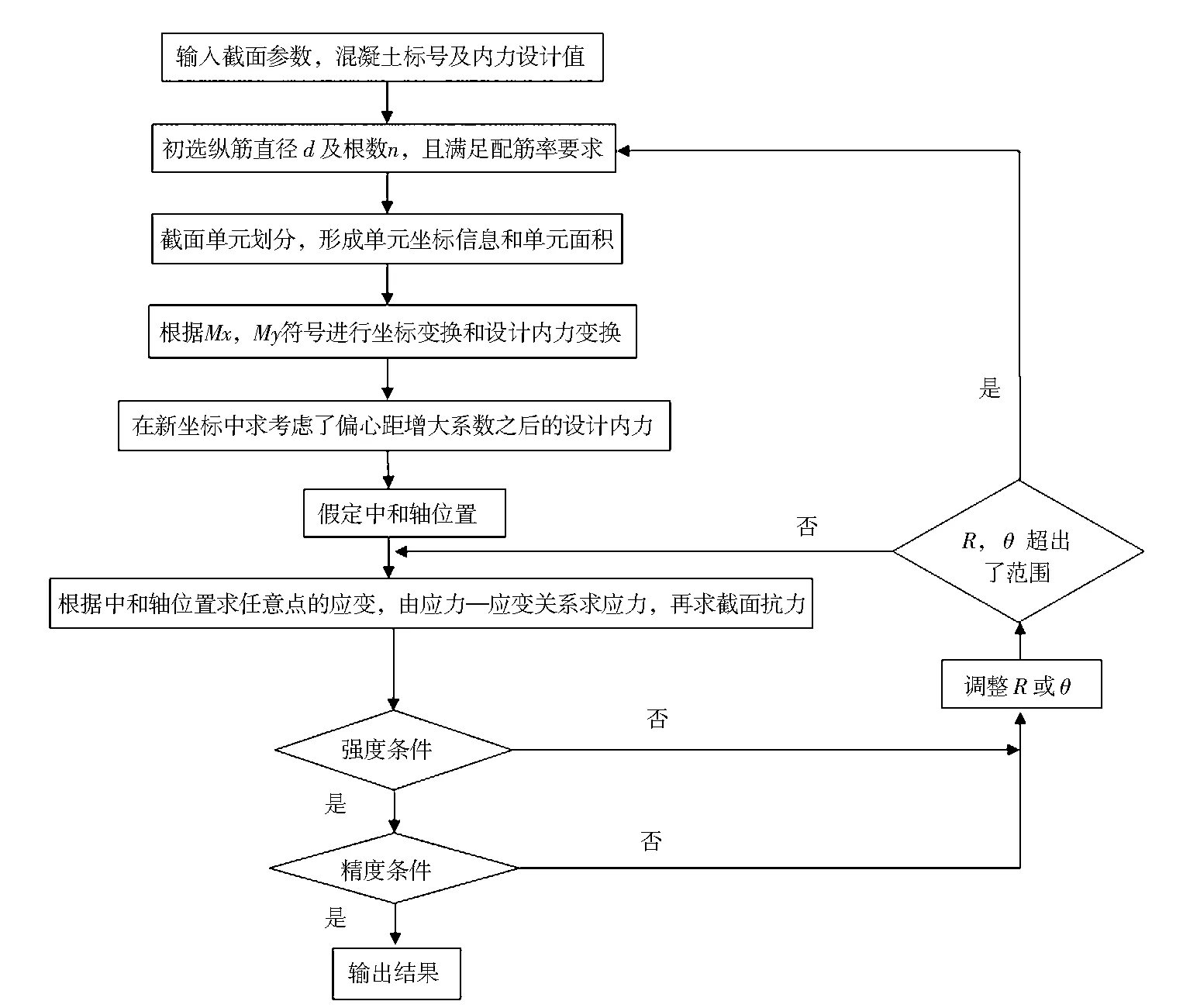
图1 数值积分法计算流程图Fig.1 Numerical integral method calculation flow chart

1.5 计算结果分析

使用2010版PKPM[7]中的结构基本构件辅助设计软件GJ来完成异形柱构件的设计计算，见表1.从表1可以看出,本研究所配钢筋与PKPM配筋较为一致，但存在一些误差，这可能是由于PKPM中混凝土应力应变曲线与本研究所取有所不同而造成的，也有很大可能是算法上的一些差异导致的，如单元划分的方法或大小、迭代方法的选取、计算精度的控制及安全系数等.

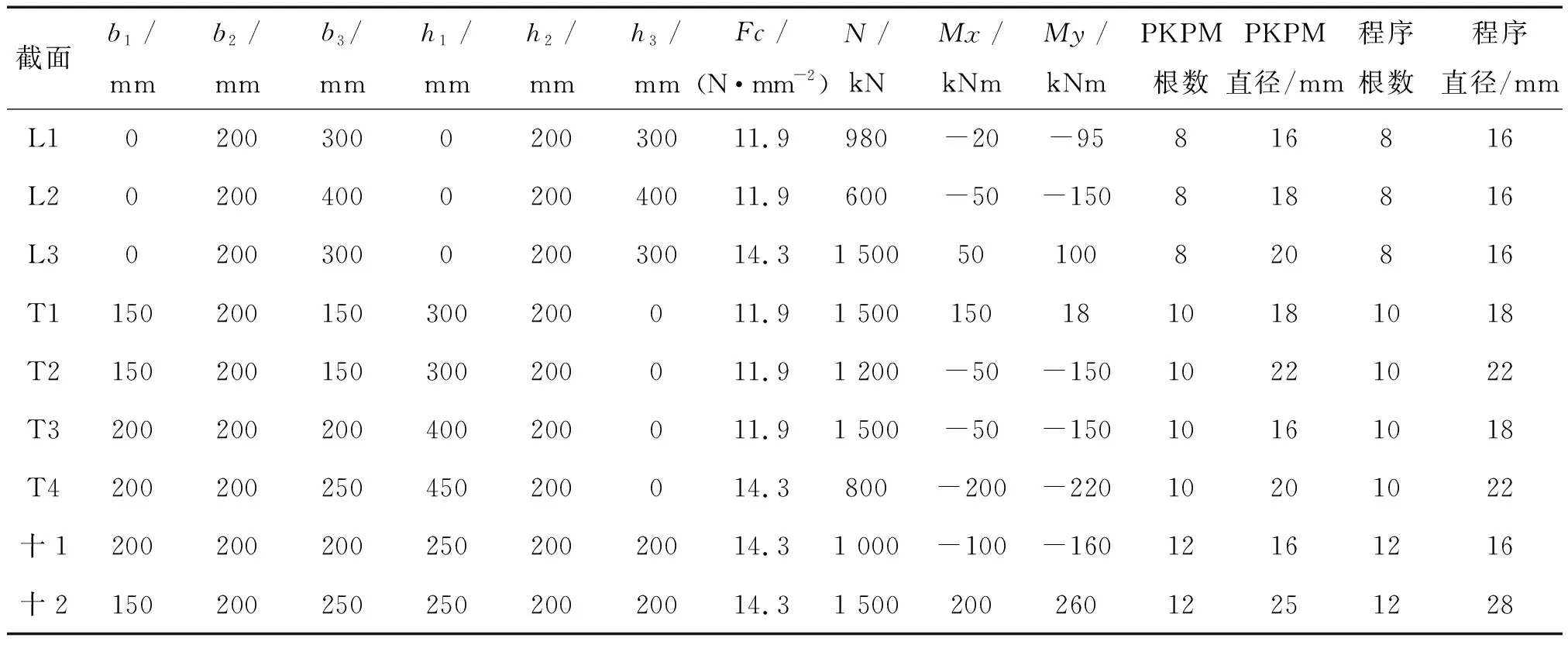
表1 配筋计算比较Tab.1 Reinforcement calculation

2 优化设计数学模型及程序设计

2.1 设计变量

异形柱框架结构多级优化的设计变量包括异形柱的截面参数b1，b2，b3，h1，h2，h3以及结构的混凝土强度等级.在优化过程中，异形柱的截面形式在优化中控制为与原设计的截面形状保持一致，如原来是L形的优化结果中截面形状依旧保持为相同方向的L形，改变的只是长度非0柱肢的尺寸，这样能够使异形柱截面优化的结果与设计思路一致.

2.2 目标函数

目标函数是设计变量的函数，本研究的目标函数为结构所有主体构件的综合造价之和(以下简称造价)，各构件的造价组成包括混凝土、钢筋、模板的造价.在框架结构中，将造价作为判定优化结果的唯一标准.

单根梁构件的造价为：

(3)

单根异形柱构件造价为：

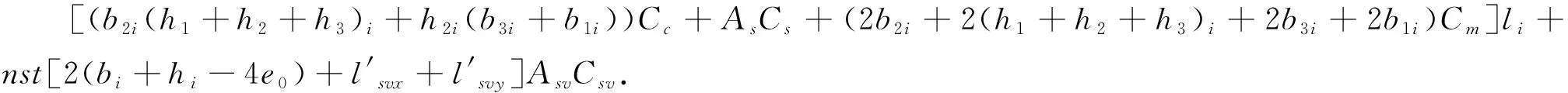
(4)

结构的总造价为：

(5)

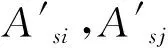
2.3 约束条件

2.3.1 强度约束

M≤Mu，

(6)

V≤Vu.

(7)

异形柱强度约束的具体计算公式按照GB 50010—2010《混凝土异形柱结构技术规范》进行.

2.3.2 刚度约束

异形柱框架结构刚度约束为每层最大弹性层间位移角满足

δi/hi<1/600.

(8)

2.3.3 构造约束

构造约束包括梁杆件截面高宽比不超过4；异形柱肢宽等于墙厚且各肢肢长要满足最小肢长和最大肢长的要求；梁、柱配筋还需要满足截面最大配筋率、最小配筋率、钢筋直径、钢筋最大间距、钢筋最小间距、箍筋肢数与柱轴压比限制等.这些构造要求全部按照GB 50010—2010《混凝土结构设计规范》进行设置，力求提高优化设计结果的可行性.

2.4 优化程序的实现

优化设计程序需要完成结构的截面尺寸及每层混凝土强度等级的选择，对每个构件进行理论配筋计算并完成钢筋的实配，最后计算整个结构的造价信息.在进行优化前，需要输入梁截面尺寸上下限与异形柱柱肢的尺寸上下限，使优化结果尽量满足实际需要.

3 算例

图2为某简单异形柱框架结构，楼面恒载为7 kN/m2,楼面活载为2 kN/m2,梁上线载为7 kN/m, 结构位于7度设防区，框架抗震等级四级，场地类别为上海IV类，场地特征周期为0.90 s，多遇地震影响系数最大值为0.04，基本风压为0.55 kN/m2.

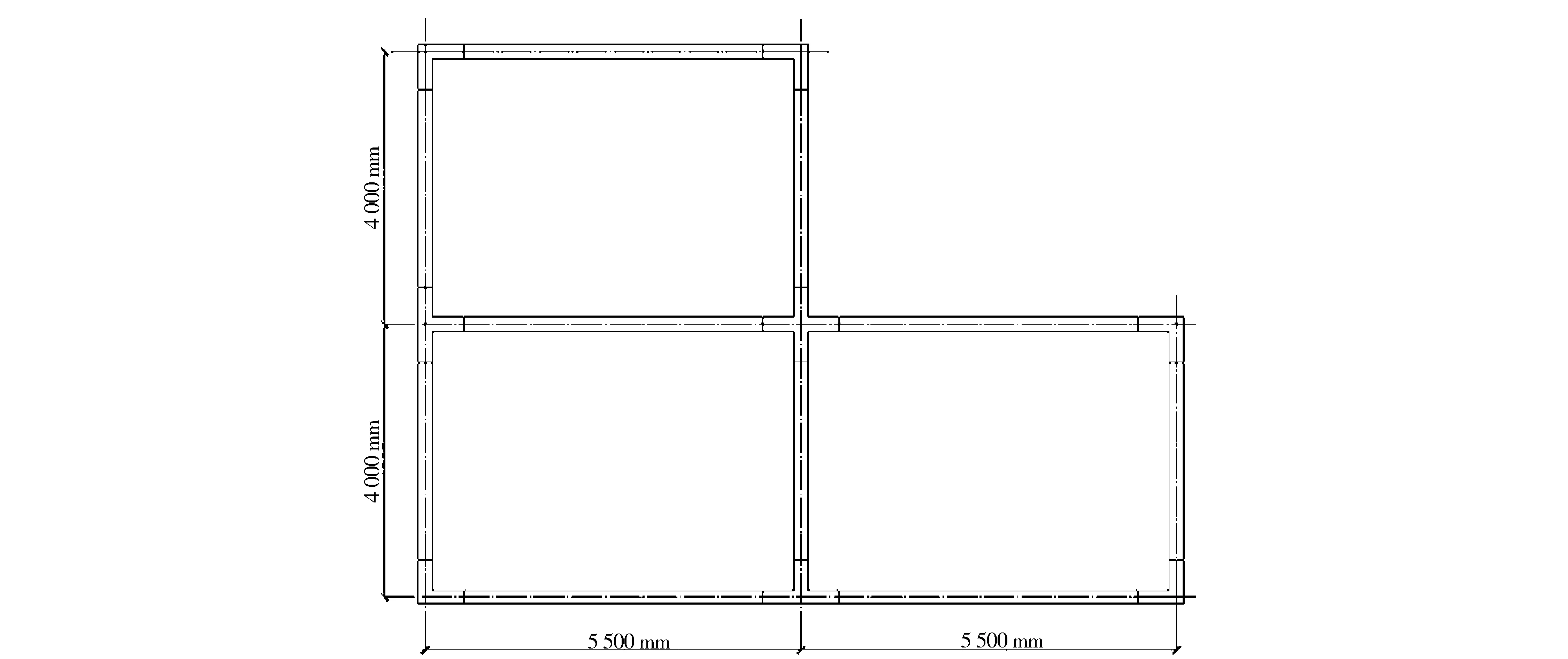
图2 算例结构示意图Fig.2 Coordinate internal force conversion

在进行优化设计前，设定柱肢截面的可接受尺寸为500～750 mm，梁截面的截面宽度恒为200 mm，与柱肢同宽.表2是Z1优化前与优化后的对比，表3是梁1优化前与优化后的对比.通过本方法进行优化设计后，结构混凝土等级从原来的C30提高到C35，原造价为45 506.7元，优化后造价为30 430.9元，造价节省率为33.13%.

表2 柱Z1优化前后对比Tab.2 Column Z1 before and after optimization contrast

表3 梁L1优化前后对比Tab.3 Beam L1 before and after optimization contrast

4 结语

本研究就解决异形柱框架结构的优化问题进行了一定的探索,运用多级优化的思想，将混凝土等级和异形柱的截面尺寸嵌入不同级别的优化过程中,该结果可为结构初步设计提供一个较经济的参考方案.

参考文献：

[1] 连星.双向偏心受压异形柱计算机辅助配筋计算[D].合肥:合肥工业大学,2006:13-17.

[2] Richard Balling. Giving Designers a Choice of Optimal Designs[C].17th Analysis and Computation Specialty Conference,2006:37.

[3] DG/TJ 08-009-2002.钢筋混凝土异型柱结构技术规程[S]:2002.

[4] GB 50010—2010.混凝土结构设计规范[S]:2010.

[5] 肖芳.异形柱正截面承载力研究及异形柱框架结构计算机辅助设计[D].长沙:湖南大学,2001:29-37.

[6] 姚俊淦,江见鲸.异形柱双向偏心受压正截面承载力分析及程序设计[J].力学与实践,2001,23(2):20-23.

[7] GJS-4结构基本构件辅助设计软件用户手册[Z].2011.

[8] 朱杰江,郑愔睿.空间钢筋混凝土框架的多级优化及程序开发[J].建筑科学,2009,25(1):91-95.