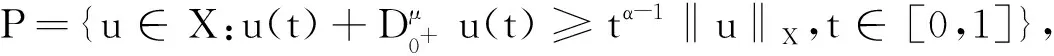一类带有p-Laplacian算子分数阶微分方程边值问题正解的存在性

申腾飞,刘文斌,宋文耀

(中国矿业大学理学院,中国 徐州 221008)

分数阶导数是整数阶导数的推广.近些年来,分数阶微分方程在自然科学及工程技术等领域得到了重要应用[1].越来越多的学者投身于分数阶微分方程的研究,取得了不少的研究成果[2-13], 文献[3]运用了不动点定理研究了一类分数阶微分方程

文献[4]运用迭合度理论研究了一类带有p-Laplacian算子的分数阶微分方程

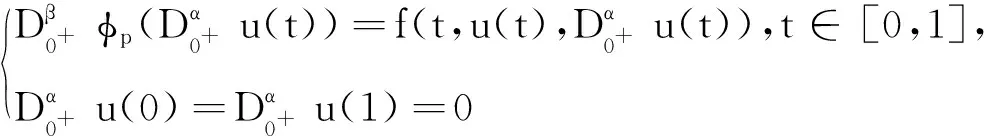
本文主要讨论以下带有p-Laplacian算子分数阶的微分方程的边值问题

(1)

1 预备知识

定义1[2]函数y:(0,+∞)→R的α阶Riemann-Liouville分数阶积分为

其中α>0,Γ(·)为gamma函数，右边在(0，∞)逐点有定义.

定义2[2]连续函数(0,+∞)→R的α阶Riemann-Liouville分数阶导数为

其中,α>0,Γ(·)为gamma函数,n=[α]+1，右边是在(0，∞)逐点有定义的.

定义3[2]设B是Banach空间,P⊂B是一个锥.θ:P→[0,+∞)是连续泛函且对一切x,y∈P和t∈[0,1],不等式θ(tx+(1-t)y)≥tθ(x)+(1-t)θ(y)成立,则称θ是P上的非负连续凹泛函.

u(t)=c1tα-1+c2tα-2+…+cNtα-N，

其中N=[α]+1,ci∈R,i=1,2,…,N.

其中N=[α]+1,ci∈R,i=1,2,…,N.

引理3[2]若α>0,如果λ>-1,λ≠α-i,i=1,2,...,[α]+1,t>0 ,那么

引理4若y(t)∈C[0,1]且3<α≤4,则分数阶微分方程

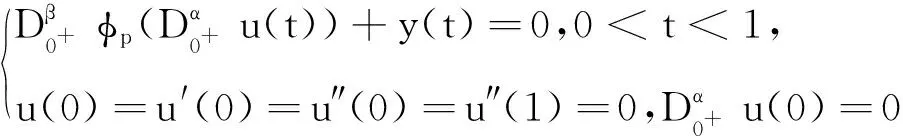
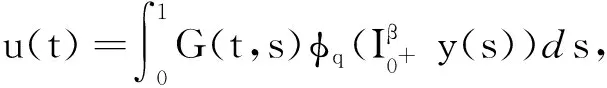
证由引理1和引理2,存在ci∈R,i=1,2,3,4使得分数阶微分方程的解等价于

由边值条件u(0)=0可得c4=0.所以

由u′(0)=0可得c3=0.所以

引理5G(t,s)有下面的性质:

(1)G(t,s)≥0,s,t∈(0,1)；(2)G(1,s)≥G(t,s)≥tα-1G(1,s),s,t∈(0,1),

证(1)当s≤t时,有t-ts≥t-s,则

Γ(α)G(t,s)=tα-1(1-s)α-3-(t-s)α-1≥tα-1(1-s)α-1-(t-s)α-1≥

(t-ts)α-1-(t-s)α-1≥0 .

故G(t,s)≥0. 当t≤s时,显然G(t,s)≥0.

(2)根据G(t,s)的定义,对于给定s∈(0,1),G(t,s)在定义区间上关于t是增函数,则G(t,s)≤G(1,s).当s≤t时,

Γ(α)G(t,s)=tα-1(1-s)α-3-(t-s)α-1≥tα-1(1-s)α-3-(t-ts)α-1=

tα-1(1-s)α-3-tα-1(1-s)α-1=tα-1[(1-s)α-3-(1-s)α-1].

则G(t,s)≥tα-1G(1,s).当t≤s时,

Γ(α)G(t,s)=tα-1(1-s)α-3≥tα-1(1-s)α-3-(t-ts)α-1=tα-1(1-s)α-3-tα-1(1-s)α-1=

tα-1[(1-s)α-3-(1-s)α-1].

则G(t,s)≥tα-1G(1,s).

引理6G(t,s)有下面的性质:

证首先证明

因为

由引理1和引理2得

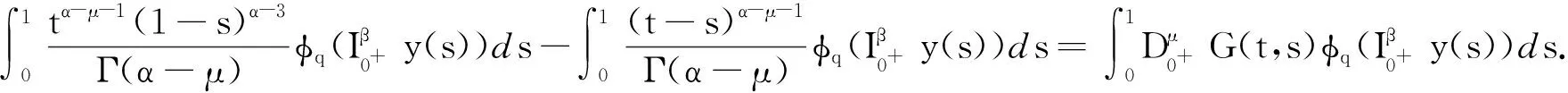
余下证明过程类似引理4,在此省略.

(i) 当u∈p∩∂Ω1时,‖Tu‖≤‖u‖；当u∈p∩∂Ω2时,‖Tu‖≥‖u‖,

(ii) 当u∈p∩∂Ω1时,‖Tu‖≥‖u‖；当u∈p∩∂Ω2时,‖Tu‖≤‖u‖.

(i) 当x∈P(θ,b,d)时,{x∈P(θ,b,d)|θ(x)>b}≠∅且θ(Tx)>b,

(iii) 当x∈P(θ,b,c)且‖Tx‖>d时,θ(Tx)>b.

那么T至少存在3个不动点x1,x2,x3且‖x1‖

注1c=d条件下(iii)可由(i)得到.

2 主要结果

下面证明T为全连续算子T:P→P.

证首先,由引理5和6知

显然T是连续算子,下面证T(P)⊂P是一致有界的.

设Ω是锥P中的有界集,Ω={u∈p|‖u‖X≤R}, 又f是连续函数,则存在正数A,使得

故‖Tu‖X是一致有界的.再证T是等度连续的.设0≤t1

因为tα-1,tα-μ-1在[0,1]是一致连续的,φq(s)在[-A,A]是一致连续的,因此T是等度连续的.由Arzela-Ascoli定理知,T(P)是相对列紧的,故T是全连续的.

为了叙述方便定义如下常数

定理1设f,g:[0,1]×[0,+∞)×R→[0,+∞)连续函数,若存在2个常数l2>l1>0 ,使得

(H1)∀(t,x,y)∈[0,1]×[0,l1)×(-∞,+∞),f(t,x,y)≥φp(Ml1) ,

(H2)∀(t,x,y)∈[0,1]×[0,l2)×(-∞,+∞),f(t,x,y)≤φp(Nl2)；

则问题(1)至少存在一个正解.

证令Ω1={u:‖u‖X

因此,当u∈P∩Ω1时,‖Tu‖X≥‖u‖X.

另一方面,令Ω2={u:‖u‖X

因此,当u∈P∩Ω2时,‖Tu‖X≤‖u‖X.

定理2假设存在常数0

(H3)∀(t,x,y)∈[0,1]×[0,a)×(-∞,+∞),f(t,x,y)<φp(Na);

(H5)∀(t,x,y)∈[0,1]×[0,c)×(-∞,+∞),f(t,x,y)≤φp(Nc);

则问题(1)至少存在3个正解.

由条件(H3)可得‖Tu‖X

即θ(Tu)>b,所以引理8(i)成立,又因为当d=c时条件(iii)可由条件(i)得到,故方程BVP(1)至少有3个正解.

参考文献:

[1] KILBAS A A, SRIVASTAVA H M, TRUJILLO J J. Theory and applications of fractional differential equations [M].Amsterdam：Elsevier, 2006.

[2] BAI Z B, LV H S. Positive solutions for boundary value problem of nonlinear fractional differential equation[J]. J Math Anal Appl, 2005,311( 2):495-505.

[3] BAI Z B. On positive solutions of a nonlocal fractional boundary value problem[J]. Nonlinear Anal, 2010,72(2):916-924.

[4] CHEN T Y, LIU W B. A boundary value problem for fractional differential equation withp-Laplacian operator at resonance [J]. Nonlinear Anal, 2012,75(6):3210-3217.

[5] SU X W. Boundary value problem for a coupled system of nonlinear fractional differential equations [J]. Appl Math Lett, 2009,22(1):64-69.

[6] GAN S Q. Dissipativity ofθ-methods for nonlinear delay differential equations of neutral type [J]. Appl Numer Math, 2009,59(6):1354-1365.

[7] SUN H R, TANG L T, WANG Y H. Eigenvalue problem forp-Laplacain three-point boundary value problems on time scales[J].J Math Anal Appl, 2007,331(1):248-262.

[8] ZHANG Y H, BAI Z B. Existence of solutions for nonlinear fractional three-point boundary value problems at resonance [J]. J Appl Math Comput, 2011,36(2):417-440.

[9] ZHAO Y G, SUN S R. The existence of multiple positive solutions for boundary value problem of nonlinear fractional differential equations [J]. Commun Nonlinear Sci Numer Simulat, 2011,16(4):2086-2097.

[10] XU X J, JANG D Q. Multiple positive solutions for the boundary value problem of a nonlinear fractional differential equation [J]. Nonlinear Anal, 2009,71(10):4676-4688.

[11] 曹 珂. 一类非线性三阶三点边值问题单调正解的存在性[J].湖南师范大学自然科学学报, 2011,34(4):14-17.

[12] 蒋明霞. 带非线性扩散项的中立双曲型方程的振动判据[J]. 湖南师范大学自然科学学报, 2011,34(6):12-16.

[13] 葛渭高. 非线性常微分方程边值问题 [M]. 北京:科学出版社, 2007.