“高考中的拉格朗日中值定理”中的一点纰漏

● (广水市第一中学 湖北广水 432700)

“高考中的拉格朗日中值定理”中的一点纰漏

●聂文喜(广水市第一中学 湖北广水 432700)

1 原文摘抄

例1[1]已知函数

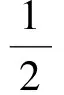
(1)讨论函数f(x)的单调性；

(2009年辽宁省数学高考理科试题)

(1)略；

(2)证法2[1]不妨设点A(x1,f(x1))，B(x2,f(x2))，原题即证f(x)的任意一条割线的斜率kAB>-1.由几何图形可知，只需证f(x)的任意一条切线的斜率kAB>-1，即证f′(x)>-1对x∈(0,+∞)恒成立，也即证

记

令h(x)=x2-(a-1)x+a-1，则

h′(x)=2x-(a-1).

从而

g(x)>0．

例2[1]已知函数

f(x)=(a+1)lnx+ax2+1．

(1)讨论函数f(x)的单调性；

(2)设a<-1，如果对任意x1,x2∈(0,+∞)，|f(x1)-f(x2)|≥4|x1-x2|成立，求a的取值范围．

(2010年辽宁省数学高考理科试题)

解[1](1)略；

(2)由拉格朗日中值定理，知必存在x0∈(0,+∞),使得

由|f(x1)-f(x2)|≥4|x1-x2|，得

f(x1)-f(x2)≥4(x1-x2)，

从而

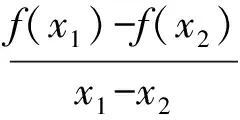
即

f′(x0)≤-4.

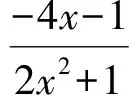
故

a∈(-∞,-2]．

2 解法分析

文献[1]的解题根据是：对于一个连续可导函数，任意一条割线都可以找到一条与其斜率相等的切线，这就是高等数学中的拉格朗日中值定理：

若函数f(x)满足如下条件：

(1)若f(x)在闭区间[a,b]上连续；

(2)若f(x)在开区间(a,b)上可导,

拉格朗日中值定理没有逆定理，即对曲线的任一切线，并不一定存在割线，使割线斜率等于切线斜率，因此A=B并不一定成立．如f(x)=x2(x∈R)，f′(x)=3x2，f′(0)=0，即f(x)在x=0处的切线斜率为0，但f(x)=x3不存在割线使割线斜率等于0．这就说明割线斜率与切线斜率并不一定等价，从而文献[1]对例2的解法存在纰漏．

3 一个反例

(2012年湖北省孝感市高三数学统考理科试题)

解法1利用拉格朗日中值定理

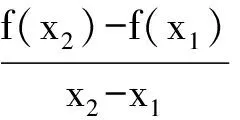
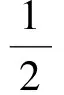
则

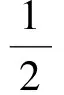
故

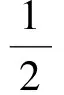
解法2利用转化思想

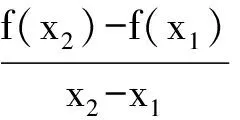
f(x2)-ax2>f(x1)-ax1

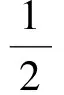
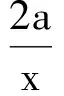
即2a≤x2-2x=(x-1)2-1在(0,+∞)恒成立，故

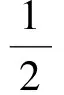
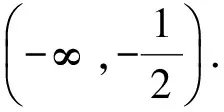
对于例3，解法2的结果是正确的，解法1的结果是不正确的，从而进一步说明：在可导曲线中，{割线斜率}={切线斜率}是一个错误的命题．

4 一个结论

利用拉格朗日中值定理易得如下结论：

结论在可导曲线y=f(x)中，其图像上任意2个不同点连线的斜率组成的集合为P，图像上任一点处的切线斜率组成的集合为Q，则

(1)P⊆Q，即{割线斜率}⊆{切线斜率}；

(2)若f(x)是定义域内的凸(或凹)函数，则P=Q，即{割线斜率}={切线斜率}；

(3)f(x)在定义域内有在唯一拐点(x0,f(x0))，则f′(x0)∉P，且P∪{f′(x0)}=Q．

综上所述，对于可导函数而言，其图像上任意2个不同点连线的斜率的取值范围与f′(x)的取值范围并不等价，前者所组成的集合只是后者所组成集合的子集，在解题时应慎用．

[1] 吴旻玲，高考中的拉格朗日中值定理[J]．中学教研(数学)，2012(7)：44-46．