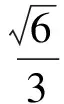数形结合速解离心率取值范围问题
● (温州市第二中学 浙江温州 325000)
数形结合速解离心率取值范围问题
●李芳奇(温州市第二中学 浙江温州 325000)
0 引言
著名数学家拉格朗日曾经说过:“只要代数同几何分道扬镳,它们的进展就缓慢,它们的应用就狭窄.但当这2门科学结合成伴侣时,它们就互相吸收新鲜的活力,从而以快捷的步伐走向完美.”《浙江省普通高考考试说明》在对创新意识的考查中明确指出:在考试中要有反映数、形运动变化的试题.在高三复习教学中,有很多求圆锥曲线离心率取值范围的问题,其中求离心率的值、求取值范围的问题由于涉及到不等式与函数等综合知识,方法灵活多变,难度相对较大.解决这类问题,可以通过代数分析运算得出,可谓是通法,然而对于学困生甚至中等生,在处理过程中往往会顾此失彼,造成丢分.离心率具有明确的几何意义,如果由“数”到“形”加以转化,解题的过程相对会便捷很多,能大大地提高解题速度和正确率.那么,如何通过数形结合来巧解离心率取值范围的问题呢?这就需要我们认真分析题目,从题目中发现问题的本质,通过临界情况的控制求解.
1 典型例题解读
1.1 以渐近线为临界位置的变化
渐近线控制着双曲线的形状,而双曲线的形状又与离心率相关,因此与双曲线离心率有关的问题,可以考虑渐近线的位置.
例1已知双曲线mx2-y2=1(m>0)的右顶点为A,若该双曲线右支上存在点B,C使得△ABC为等腰直角三角形(如图1),则该双曲线的离心率e的取值范围是________.
(2011年温州市高三数学第一次适应性测试理科试题)
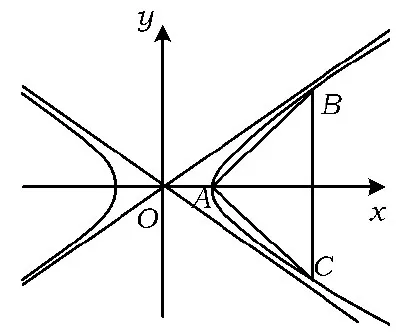
图1

图2
解法1根据双曲线的对称性,可知A为△ABC的直角顶点,要求双曲线右支上存在点B,C使得△ABC为等腰直角三角形,则过点A作倾斜角为45°的直线与双曲线的交点即为点B.由
得

因为

且

所以
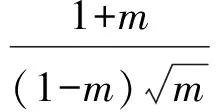
得
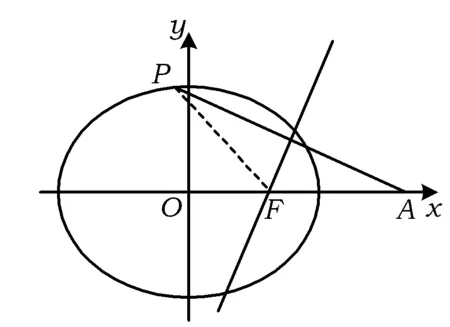
0 从而 e2=1+m∈(1,2), 得 点评解法1根据直线与双曲线的位置关系,联立并采用韦达定理求根,通过根的范围加以限制,进而求出m的取值范围.而解法2是对双曲线渐近线加以控制,无需联立求根,虽然对思维的要求相对要高一些,但运算量很小,经过这样的训练后,学生也较容易掌握. (浙江省东阳中学2012届高三10月阶段性数学考试理科试题) 得 点评根据例1的启发,研究双曲线的渐近线可控制双曲线的形状.此题需注意右焦点F的对称点在y轴,则直线OP方程为y=x,不存在点P,即直线与双曲线无交点.看似繁难的问题,实则解答步骤很简捷.在答题时应注意分析题意,抓住解决问题的关键点. 1.2 角度、长度的变化控制 图3 解法1设|PF1|=m,|PF2|=n,由椭圆第一定义知,m+n=2a.由余弦定理可得 4c2=m2+n2-2mncos120°, 于是 (m+n)2-mn=4c2, 从而 得 3a2≤4c2, 即 解法2由直观经验可知,当点P在短轴端点A处时,∠F1PF2最大(过程可以证明,思路参照解法1,设|PF1|=m,|PF2|=n,根据余弦定理的变形公式 可知当且仅当m=n时,∠F1PF2最大).椭圆上恒存在一点P,使得∠F1PF2=120°,则∠F1AO≥60°,即 于是 即 点评解法1根据椭圆的第一定义,采用基本不等式求取值范围,过程严谨而周密.解法2由直观经验可知,在短轴端点处取到最值,而当P从点A移动到点B时,∠F1PF2越来越小.大量的解题经验和扎实的基础知识会使我们在解题过程中产生直觉思维,直觉思维的产生需要细致入微的观察力,它帮助我们寻找到解题的最快途径.但直观经验有可能得出错误的结论,与严密的推理相结合才能相得益彰.例3的变式题由于∠F1PF2=90°,可以通过作圆快速求解. 图4 (2010年四川省数学高考理科试题) 解由题意得 且 a-c<|PF|≤a+c, 因此 得 a2-ac-2c2≤0, 从而 2e2+e-1≥0, 于是 点评充分挖掘题目中的几何性质,紧抓椭圆中线段长度的有界性,摒弃繁琐的代数运算.求离心率的取值范围的问题,要保留a,c这2个基本量. 2.斜率为2的直线过中心在原点且焦点在x轴上双曲线的右焦点,与双曲线的2个交点分别在左右两支上,求双曲线离心率的取值范围. 参考答案 [1] 王晓青.用运动观点探求圆锥曲线离心率的取值范围[J].中国数学教育,2011(6):40-41. [2] 武增明.走进圆锥曲线离心率的取值范围的思维途径[J].中学数学,2009(11):3-5.


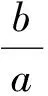




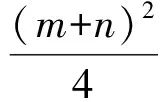










2 精题集萃