一个几何不等式的应用及推广

● (开化县第二中学 浙江开化 324300)

一个几何不等式的应用及推广

●曹嘉兴(开化县第二中学 浙江开化 324300)

近日，笔者探究了一个简单而重要的几何不等式，它是著名的外森比克不等式的一种加强，利用该不等式及其证明可以得出一些非常有趣的不等式.当笔者进一步研究该不等式的推广时发现，我们所熟知的一些重要不等式都可由其推广得到.

定理1设△ABC的3条边长和面积分别为a,b,c和Δ，则

当且仅当△ABC为正三角形时等号成立.

证明在△ABC中,由余弦定理得

c2=a2+b2-2abcosC,

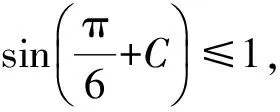
(a+b)2-4ab=(a-b)2≥0,

即

显然，当且仅当△ABC为正三角形时等号成立.

推论1[1]设△ABC的3条边长和面积分别为a,b,c和Δ，则

证明由二元均值不等式及本文定理1可得

推论1就是著名的外森比克不等式,本文定理1是外森比克不等式的一种加强.

推论2设△ABC的3条边长和面积分别为a,b,c和Δ，则

证明从本文定理1的证明可以看出有以下更强的不等式:

同理可得

把式(1),(2),(3)相加立即得到推论2.

推论3设△ABC的3条边长、3个内角和面积分别为a,b,c；A,B,C和Δ，则

证明从本文定理1的证明可知

同理可得

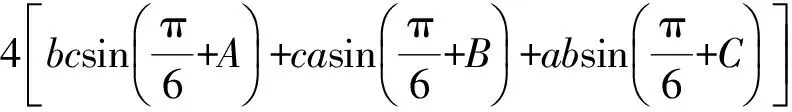
(7)

由费恩斯列尔─哈德维格尔不等式[1]：

a2+b2+c2≥

可得

因此

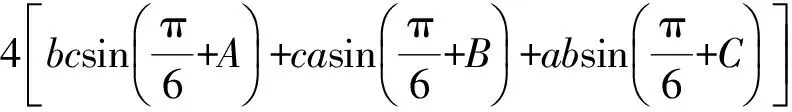
推论3是一个非常有趣的不等式，它将三角形的所有基本元素(3条边长、3个內角和面积)融于一体.

推论4设△ABC的3个内角分别为A,B,C，则

把定理1推广到2个三角形中，便得到

定理2设△ABC和△A′B′C′的3条边长和面积分别为a,b,c，Δ；a′,b′,c′，Δ′，则

2aba′b′+c2c′2≥16ΔΔ′，

当且仅当△ABC和△A′B′C′都是正三角形时等号成立.

证明由正弦定理得

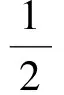
利用三元均值不等式得

即

2aba′b′+c2c′2≥16ΔΔ.

由以上证明过程不难看出当且仅当△ABC和△A′B′C′都是正三角形时等号成立.

推论1[2]设△ABC和△A′B′C′的3条边长和面积分别为a,b,c，Δ；a′,b′,c′，Δ′，则

a2a′2+b2b′2+c2c′2≥16ΔΔ′,

等号当且仅当△ABC和△A′B′C′都是正三角形时成立.

证明由二元均值不等式及本文定理2可得

a2a′2+b2b′2+c2c′2≥2aba′b′+c2c′2≥16ΔΔ′.

推论2[1]设△ABC和△A′B′C′的3条边长和面积分别为a,b,c，Δ；a′,b′,c′，Δ′，则

等号当且仅当△ABC和△A′B′C′都是正三角形时成立.

证明由本文定理2得

同理可得

把式(8),(9),(10)相加得

(aa′+bb′+cc′)2≥48ΔΔ′,

即

利用定理2的证法还可以对定理1中的不等式作加权推广，便得到以下结论.

定理3设△ABC的3条边长和面积分别为a,b,c和Δ;λ，μ为任意正数，则

等号当且仅当λ=μ并且△ABC为正三角形时等号成立.

即

由以上证明过程不难看出当且仅当λ=μ并且△ABC为正三角形时等号成立.

推论设△ABC的3条边长和面积分别为a,b,c和Δ，则

等号当且仅当△ABC为正三角形时成立.

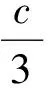
即

这个推论就是著名的波利亚─舍贵不等式[3].

[1] 匡继昌.常用不等式[M].3版.济南：山东科学技术出版社，2004.

[2] 单墫．几何不等式[M]．上海：上海教育出版社，1980：55．

[3] 单墫．数学名题词典[M]．南京：江苏教育出版社，2002：543．

[4] 杨学枝．数学奥林匹克不等式研究[M]．哈尔滨：哈尔滨工业大学出版社，2009．

[5] 安振平.从著名的外森比克不等式引发的思考[J]．中学教研(数学),2010(10)：23-25.