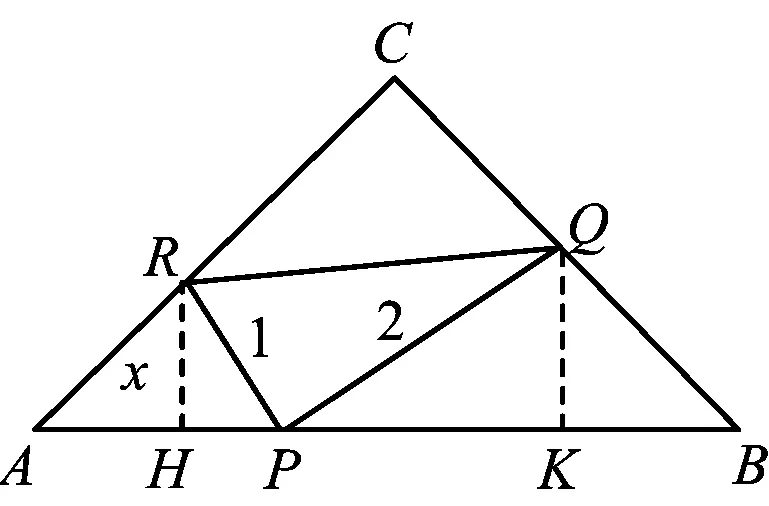
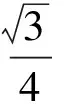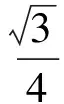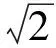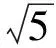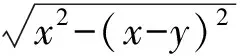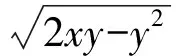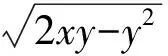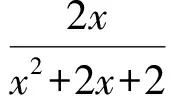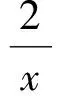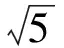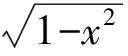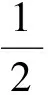数学竞赛中的几何最值问题
● (镇海蛟川书院 浙江宁波 315201)
数学竞赛中的几何最值问题
●刘清泉(镇海蛟川书院 浙江宁波 315201)
几何中的最值问题广泛存在于初中数学竞赛中,这类问题具有很强的探索性,需要运用动态思维以及数形结合等思想方法.几何最值问题常用的解决策略有2类:一是利用几何中不等量的性质(如“两点之间线段最短”、“垂线段最短”等)求解,求解时运用平移、轴对称和旋转等几何变换;二是借助代数方法,建立方程、函数模型求最值.
1 利用几何中不等量的性质
1.1 直接利用不等量的性质
例1在△ABC中,∠A=120°,BC=6,若△ABC的内切圆的半径为r,则r的最大值为
( )
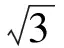
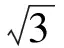
(2011年天津市初中数学竞赛试题)
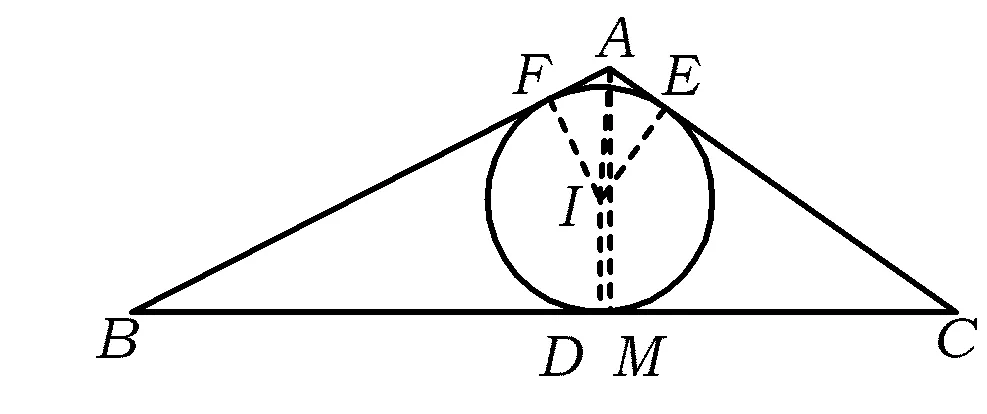
图1
解如图1,设⊙I分别切△ABC的3条边于点D,E,F,联结IA,ID,IE,IF,并作AM⊥BC.易得
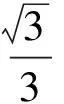

得
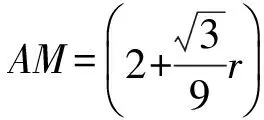
由AM≤AI+ID,得

评注作为一道选择题,寻找极端情形容易确定取得最值的情形,其求解过程实际上是利用了“垂线段最短”这一不等量的性质.
1.2 利用“平移变换”
例2点P在锐角△ABC的边上运动,试确定点P的位置,使PA+PB+PC最小,并证明你的结论.
解点P在锐角△ABC最短边上的高的垂足位置时,PA+PB+PC最小.
证明如下:
如图2,P为△ABC一边BC边上的高的垂足,而Q为BC边上不同于点P的任意一点.因为
PA+PB+PC=PA+BC,QA+QB+QC=QA+BC,
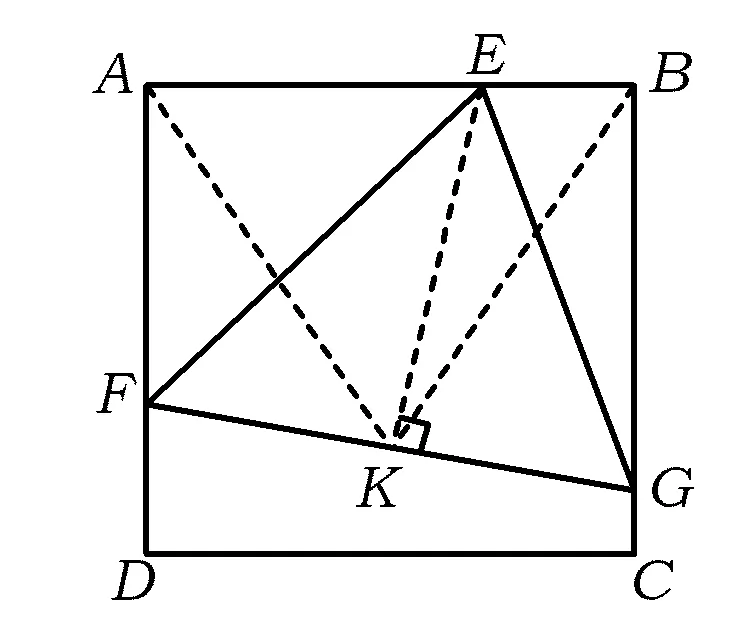
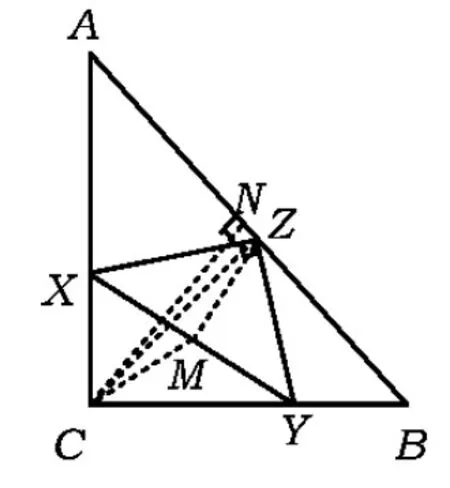
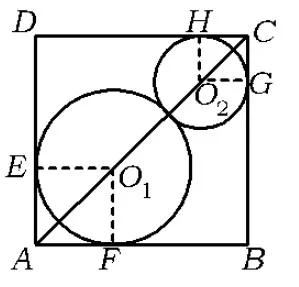
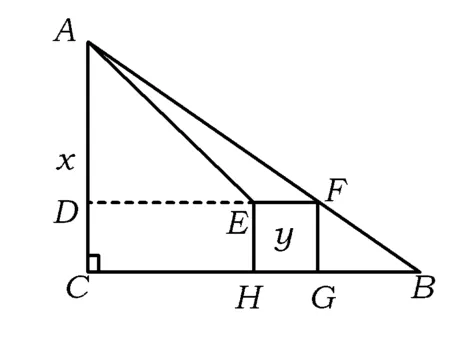
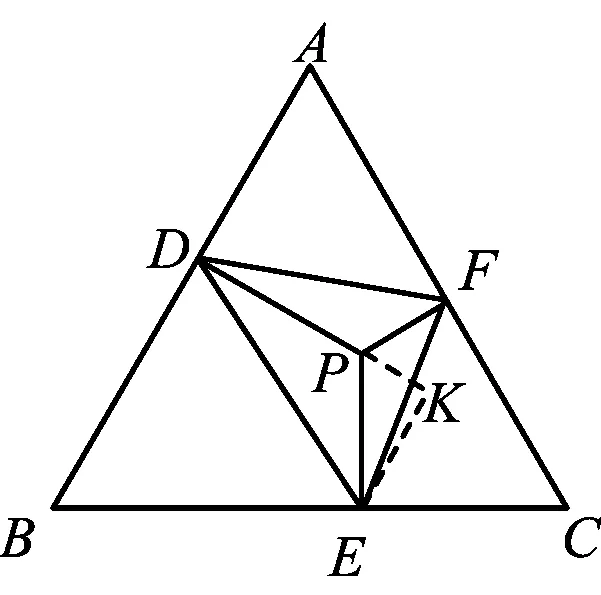
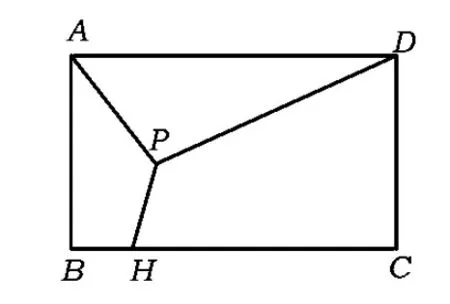
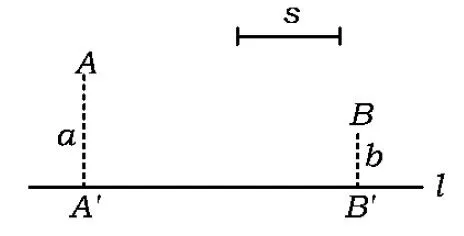
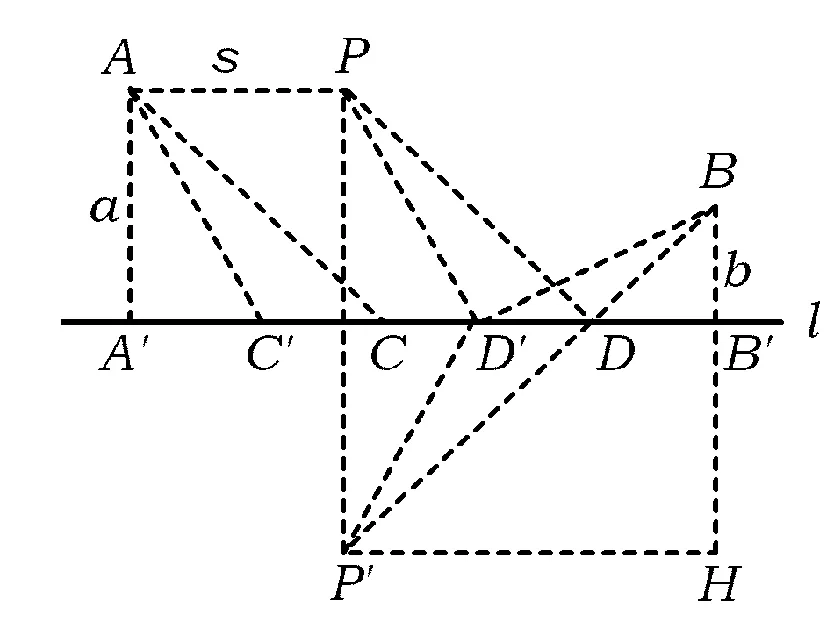
且PA PA+PB+PC 图2 图3 如图3,设AC为△ABC最短边,作BP′⊥AC,可知BP′>AP.在BP′上截取QP′=AP,在BC上截取B′C=AC,作B′Q′⊥AC,垂足为Q′,联结QB′.易证Rt△APC≌Rt△B′Q′C,得AP=B′Q′=QP′, 从而易证四边形B′QP′Q′是矩形,故∠B′QB=90°. 在△BQB′中,BB′>BQ. 因为 P′A+P′B+P′C=BQ+AP+AC, PA+PB+PC=BB′+AC+AP, 所以 P′A+P′B+P′C 评注本题通过构造矩形使线段“平移”传递,更一般地,通过构造平行四边形,借助对边平行且相等使线段平移. 1.3 利用“轴对称变换” ( ) (2008年北京市初二数学竞赛试题) 解该问题等价于直角坐标系中,在x轴上找到一点C,在直线y=x上找到一点D,使折线段BCDA最短.作点A关于直线y=x的对称点A′(-2,-1),作点B关于x轴的对称点B′(4,1),得到直线A′B′: 评注本题首先借助轴对称变换,将“两定点间的折线段最短”问题转化为“两点之间线段最短”的问题,而后结合一次函数的相关知识求解. 1.4 利用“旋转变换” 例4如图4,矩形ABCD是一个长1 000 m,宽600 m的货场,A,D是入口.现拟在货场内建一个收费站P,在铁路线BC段上建一个发货站H.设铺设公路AP,DP以及PH之长度和为l. (1)求l的最小值; (2)请指出当l取最小值时,收费站P和发货站台H的几何位置. (2011年北京市初二数学竞赛试题) 图4 图5 解(1)如图5,将矩形ABCD绕点A顺时针旋转60°到矩形AB′C′D′的位置,则矩形内的点P和边BC上的点H随之分别旋转到点P′,H′,即有 AP=AP′=PP′,P′H′=PH, 从而 l=PD+PA+PH=DP+PP′+P′H′ (即定点D到定直线B′C′上一点H′之间的距离),其最小值为点D到直线B′C′的距离DM.经计算可得 (2)当铺设公路总长取得最小值时,点H′与点M重合,点D,P,P′,H′共线,∠APD=120°.因为∠DAD′=60°,所以∠ADM=30°,故∠DAP=30°.此时,收费站P的位置在以AD为底边、两底角为30°的等腰三角形的顶点处,发货站台H的位置在边BC的中点. 评注利用旋转变换将“丫”字型线段组转化为定点与定直线上一点间的折线段,利用“垂线段最短”确定取得最值的情形,借助三角形的相关知识求出这个最值. 1.5 利用多种变换 例5如图6,河岸l同侧的2个居民小区A,B到河岸的距离分别为am,bm,A′B′=cm.现欲在河岸边建一个长度为sm的绿化带CD(宽度不计),使C到小区A的距离与D到小区B的距离之和最小.在图7中画出绿化带的位置,并写出画图过程. 图6 图7 (第21届江苏省初中数学竞赛试题) 图8 解如图8,作线段AP∥l,使AP=s,且点P在点A的右侧.取点P关于l的对称点P′,联结BP′交l于点D,在l上点D的左侧截取DC=s,则CD即为所求绿化带的位置. 下证此时AC+BD最小.设绿化带建于另一位置C′D′,联结BD′,PD′,AC′,P′D′.由对称性知 P′D=PD,P′D′=PD′. 由APCD及APC′D′,知 AC=PD,AC′=PD′, 但 P′D′+D′B≥P′B=P′D+BD, 即 PD′+D′B≥PD+DB, 亦即 AC+BD≤AC′+BD′, 当且仅当点D′在线段P′B与l的交点时等号成立. 评注本题在“CD长度不变”的前提下,首先借助平移变换转化为常见的“折线段最短”问题,而后借助轴对称变换使问题得以解决. 2.1 寻找极端情形,利用方程求解 例6如图9,正方形ABCD的边长为1,点E,F,G分别在边AD,AB,DC上(可与顶点重合).若△EFG是等边三角形,求△EFG面积的最大值和最小值. (2010年武汉市初中数学竞赛试题) 图9 解如图9,作EK⊥FG,则K是FG的中点,联结AK,BK.由∠EKG=∠EBG=∠EKF=∠EAF=90°,得点E,K,G,B和点E,K,F,A分别共圆,故 ∠KBE=∠EGK=60°, ∠EAK=∠EFK=60°, 则△ABK为正三角形,即点M为定点. 当FG∥AD时,△EFG的面积最小,此时 FG=AD=1, 当点F与点B或点G与点C重合时,△EFG的面积最大,此时 △CBF≌△CDE. 设BF=DE=x,则 AE=AF=1-x. 在△AEF中,由AE2+AF2=EF2得 (1-x)2+(1-x)2=x2+1, 解得 因为 x<1, 所以 此时 2.2 建立一元二次方程模型,利用“根的判别式”求最值 例7已知△XYZ是直角边长为l的等腰直角三角形(∠Z=90°),它的3个顶点分别在等腰Rt△ABC(∠C=90°)的3条边上.求△ABC直角边长的最大可能值. (2002年上海市初中数学竞赛试题) 图10 图11 解如图10,若顶点Z在斜边AB上,取XY的中点M,联结CM,ZM,CZ,并作AB边上的高CN,则 CN≤CZ≤CM+MZ= 故 如图11,若顶点Z在直角边CA(或CB上),由对称性,不妨设点Z在CA上,设CX=x,CZ=y,并过点Y作YH⊥CA于点H.易证△ZYH≌△XZC,得 HZ=CX=x,HY=CZ=y. 显然△AHY为等腰直角三角形,得AH=y.设AC=b≥0,则2y+x=b,即x=b-2y.在△XZC中,由勾股定理,得 y2+(b-2y)2=12, 即 5y2-4by+b2-1=0. 评注本题需要分点Z在△XYZ的斜边上和直角边上2种情况讨论,借助几何方法(不等量的性质)和代数方法(建立方程模型)求解. 2.3 建立二次函数模型求最值 例8(1)如图12,在正方形ABCD内,已知2个动圆⊙O1与⊙O2互相外切,且⊙O1与边AB,AD相切,⊙O2与边BC,CD相切.若正方形的边长为1,⊙O1与⊙O2的半径分别为r1,r2. ①求r1与r2的关系式; ②求⊙O1与⊙O2面积之和的最小值. (2)如图13,若将(1)中的正方形ABCD改为一个宽为1、长为1.5的矩形,其他条件不变,则⊙O1与⊙O2的面积和是否存在最小值.若不存在,请说明理由;若存在,请求出这个最小值. (2010年天津市初中数学竞赛试题) 图12 图13 故⊙O1与⊙O2面积之和 (2)在Rt△OO1O2中,易得 (r1+r2)2=(1-r1-r2)2+(1.5-r1-r2)2, 整理得 当且仅当r1=r2,即⊙O1与⊙O2是等圆时,S的最小值为 2.4 建立分式函数模型求最值 例9如图14,在Rt△ABC中,∠C=90°,BC=2,AC=x,点F在边AB上,点G,H在边BC上,四边形EFGH是一个边长为y的正方形,且AE=AC. (1)求y关于x的函数解式; (2)当x为何值时,y取到最大值,并求出y的最大值. (2007年新知杯上海市初中数学竞赛试题) 图14 解(1)延长FE交AC于点D,得 由DF∥BC,得 Rt△ADF∽Rt△ACB, 于是 得 两边平方并整理得 (x2+2x+2)y2-(x3+2x2+4x)y+2x2=0, 即 (y-x)[(x2+2x+2)y-2x]=0, 得 (2)由第(1)小题,得 2.5 建立根式函数模型求最值 (2001年上海市初中数学竞赛试题) 图15 解作RH⊥AP,QK⊥PB.设RH=x,则 由Rt△PRH∽Rt△QPK,得 从而 于是 故 由 评注在勾股定理、相似三角形等相关等量关系的基础上建立变量x,y的函数关系,得到含有根式的函数并进一步求其最值. 2.6 建立多元函数模型求最值 图16 例11如图16,边长为2的正△ABC内有一点P,它到3条边的距离分别为PD,PE,PF.求: (1)PD+PE+PF的值; (2)PD2+PE2+PF2的最小值; (3)△DEF面积的最大值. (2006年日本东京巢鸭高中招生试题) 得 (2)记PD=x,PE=y,PF=z,则 从而PD2+PE2+PF2=x2+y2+z2= (3)过点E作EK⊥DP,交DP的延长线于点K,则 从而 同理 故 因为xy+yz+zx= 评注题目中涉及3个量PD,PE,PF,在第(1)小题的基础上引用2个作为变量来刻画第(2)小题中的PD2+PE2+PF2和第(3)小题中的△DEF的面积,建立多元函数模型,利用“主元法配方”确定最值.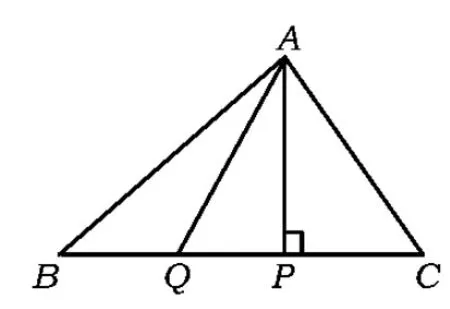

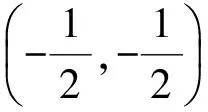



2 建立方程、函数模型