抓住3个惯性 实现师生双赢——换个角度看课堂教学成本

(平潮高级中学 江苏南通 226361)

抓住3个惯性实现师生双赢
——换个角度看课堂教学成本

陆志强(平潮高级中学 江苏南通 226361)

新课程实施以来，许多教师的教学活动充满了新意与生气．但同时，我们注意到教师课堂教学中不计“成本”的现象频现，这不能不引起我们的思考．课堂教学是否需要讲求成本？答案是肯定的．教育是一种培养人的行为，课堂教学是一种有目的、讲求效益的活动．教师在课堂教学中应牢固树立“成本意识”，抓住问题惯性、方法惯性和思维惯性，真正把学生当作学习的主体，改变教师的角色意识，全心全意为学生服务，充分利用课堂教学时间，尤其是课堂中学生的实用学习时间，达到减负增效的目的,同时使整个课堂教学形成共识、共享、共进的氛围，最终实现师生共同提高．

1 抓住问题惯性，降低审题成本

“问题是数学的心脏，是学生思维的核心”．一堂课中，教师总会围绕教学内容，针对学生知识和能力的实际提出诸多问题，以期激发学生的求知欲，启迪学生的思维，提高解题能力．问题惯性就是设计的问题前后之间要有紧密的联系，形成一个问题链或问题串，使学生在审题时，在理解问题的背景意义上不需要花费大量的时间和精力．教师在课堂教学中充分利用问题惯性，精心设置问题串，既可以降低学生审题的成本，还可以引导学生深入地分析问题、解决问题、建构知识、发展能力．

案例1在人教版《数学》七年级下册“7.1.2三角形的高、中线与角平分线”的习题课中，笔者安排了以下问题：

问题1如图1，在△ABC中，AE是高，AD是角平分线，∠B=25°，∠C=45°，试求∠DAE的度数．

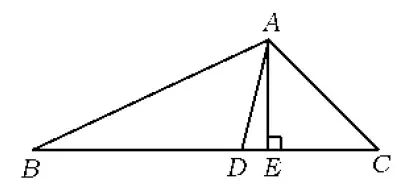
图1

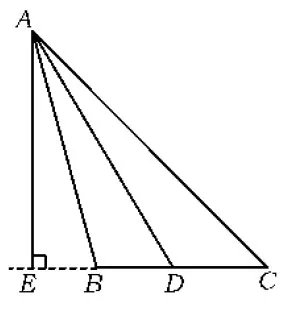
图2

问题2问题1中∠DAE，∠B，∠C之间有何数量关系？

对于问题2，大部分学生都能得出结果

问题3如图2,若∠B=105°，其他条件不变，∠DAE，∠B，∠C之间是否仍具有上述关系？

对于问题3，类比问题2，学生能发现

同时注意到∠DAE与∠B，∠C的大小有关．

问题4结合上述问题的解决，你能确定一般情况下，∠DAE，∠B，∠C之间的关系吗？

学生在进一步讨论的基础上，将结论统一为

从而总结出“任意三角形一边上的高与这边所对角的平分线的夹角等于和这边相邻两内角之差的绝对值的一半”．

问题5如图3～5，若将点A沿角平分线AD所在的直线移动至点F，过点F作FE⊥BC于点E，则∠DFE，∠B，∠C还具有上述关系吗？

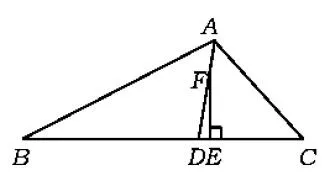
图3

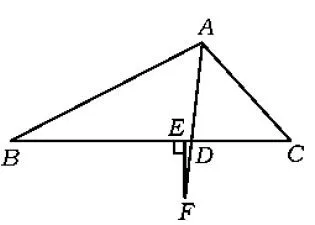
图4

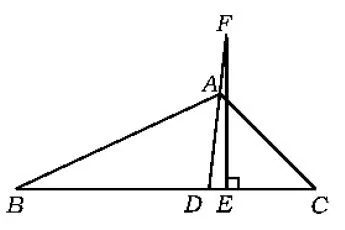
图5

上述一组问题充分利用了问题的惯性，由特殊到一般，由角度的变化到点的位置移动逐渐展开探究，开阔了学生的视野，激发了学生的求知欲，充分发挥了学生的想象力和创造力.而充分利用问题惯性，大大降低了学生的审题成本，让学生在同一问题情境中积极思考和探究，教师始终围绕着学生的学而展开，增强了学生的参与意识，培养了学生发现问题、解决问题的能力．同时，课堂效率得到进一步提高．

2 抓住方法惯性，降低时间成本

方法惯性是在解题方法或思考方式上，前后问题所采用的解题方法、思考方式可以进行类比或平移．课堂教学中利用方法惯性精心设置问题组，有利于学生顺利找到解决问题的方法和思路，大大降低了学生为探求解题思路所花费的时间，从而增加了教学时效性，提高了课堂效率．

案例2数学中考第2轮专题复习“化归思想”，现笔者撷取课堂中设计的2个问题组加以说明：

问题组1

问题1如图6，在正方形ABCD中，M是BC边(不含端点B，C)上任意一点，P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN．

证明在边AB上截取AE=MC，联结ME．在正方形ABCD中，∠B=∠BCD=90°，AB=BC,从而

∠NMC=180°-∠AMN-∠AMB=

180°-∠B-∠AMB=

∠MAB=∠MAE．

(余下的证明过程略,请读者完成.)

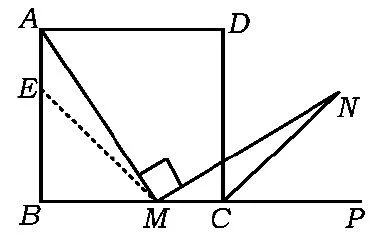
图6

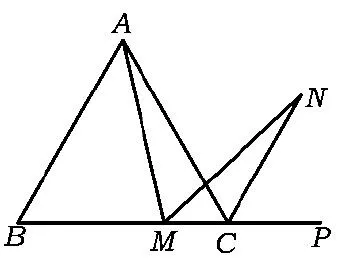
图7

问题2若将问题1中的“正方形ABCD”改为“正△ABC”(如图7)，N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由．

问题3若将问题1中的“正方形ABCD”改为“正n边形ABCD…X”，请作出猜想：当∠AMN=______°时，结论AM=MN仍然成立．

问题组2

问题1如图8，分别以Rt△ABC的3条边为直径向外作3个半圆，其面积分别用S1，S2，S3表示，探求S1,S2,S3之间的关系．

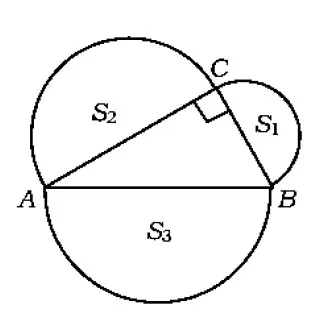
图8

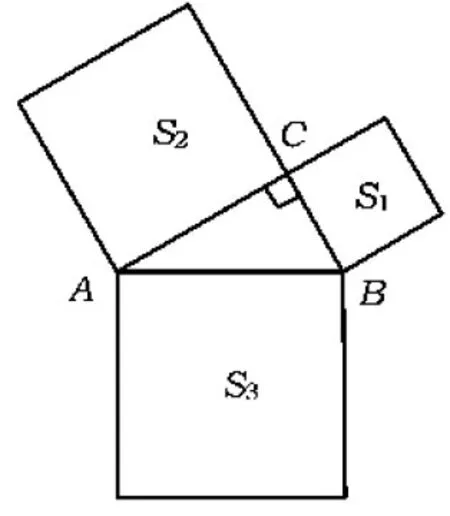
图9

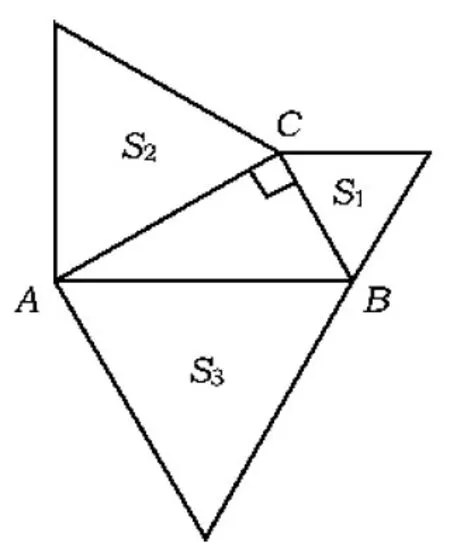
图10

问题2如图9，分别以Rt△ABC的3条边为边向外作3个正方形，其面积分别用S1，S2，S3表示，那么S1，S2，S3之间有什么关系？

问题3如图10，分别以Rt△ABC的3条边为边向外作3个正三角形，其面积分别为S1，S2，S3表示，请确定S1，S2，S3之间的关系，并加以证明．

问题4若分别以Rt△ABC的3条边为边向外作3个一般三角形，其面积分别用S1，S2，S3表示，为使S1，S2，S3之间仍具有与问题3相同的关系，所作三角形应满足什么条件？证明你的结论；

问题5类比上述结论，能总结出一个更具一般意义的结论吗？

问题组1和2均是转化为或类比问题1的基本方法加以解决，学生利用“方法惯性”，达到做一题，会一类，通一片，使他们能更好地认识问题的本质，掌握规律，也使数学课堂的解题教学达到既让学生跳出题海，又能促进他们独立思考与探究，提升了学生的解题能力．“方法惯性”的利用，在降低课堂教与学的时间成本的同时，也减轻了学生的学习负担．

3 抓住思维惯性，蓄积心智成本

学生知识的掌握与否、理解得深浅与否、能否学会迁移等，全靠平时教学中注重思维的启迪、思维的开发和思维的提升．“思维惯性”就是在思考问题的时候，思维强度有一个明显的从低到高、从表层到深刻、从简单到复杂的过程，思维活动符合正态分布规律．在课堂教学中，充分利用“思维惯性”，让学生在探究知识的同时，心智水平也得以进一步提高．

案例3人教版《数学》九年级上册第47页探究3的教学：

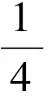
学生对这一问题情境很熟悉，但问题中未知量多，关系复杂，是教学中的难点，于是笔者设计了以下探究问题：

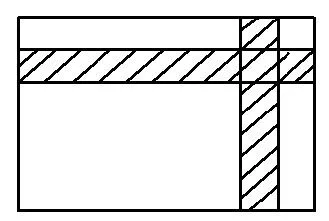
图11

图12

问题1如图11，在长30 m、宽20 m的矩形地面上修建2条同样宽的道路，余下部分作为草坪，且草坪面积需要551 m2，修建的道路宽是多少？

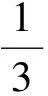
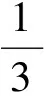
图13

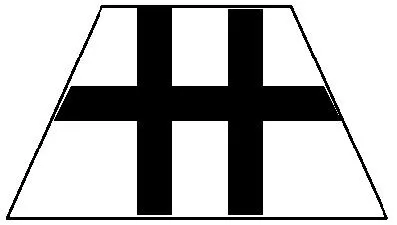
图14

问题1设置的目的是让学生发现解决此类问题最简单的方法是“平移凑整”，问题2中横、竖小路的宽度比显性化，通过与问题3对比，发现问题3解决的关键是获得横、竖小路的宽度比，从而也就能顺利解决教材中的探究问题．在此基础上，还可以进一步将问题拓展：

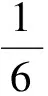
问题4实质上将其转化为问题2来解决，其思维层次更高，但有前面的“思维惯性”，大多学生还是能顺利解决的．这样处理后，课堂容量(特别是思维容量)大大增加，学生的思维活动逐步趋向深入，学生一直处于兴奋状态，课堂效益得以极大的发挥．当然，这也要求教师提高自己的心智成本，着眼于教学理念的内化，实现师生共同发展．

总之，给学生以更大的思维空间、更多的自主学习空间和更广阔的探究活动空间，教学过程中牢固树立“以人为本”的教学理念，在组织学生参与数学活动中体现数学本质，使学生真正体悟到数学的真谛．这需要教师不断提升自身素养，提高教学技能，具备高超的驾驭课堂教学的能力，体现共同发展的教育价值取向，实现师生的“双赢”．

[1] 中华人民共和国教育部．全日制义务教育数学课程标准(实验稿)[M]．北京：北京师范大学出版社，2001．

[2] 教育部课程教材研究所．义务教育课程标准实验教科书《数学》九年级上册[M]．北京：人民教育出版社，2004．

[3] 张合远．精心设计问题串 提高教学有效性[J]．中国数学教育，2010(7/8)：39-40.

[4] 陆志强．摭谈数学教学中的“适时铺垫”[J]．中学数学月刊，2012(4)：26-27.