基于Matlab的受试者操作特征曲线分析

邵毅，邵慧妍，陈卉

首都医科大学 生物医学工程学院，北京 100069

0 前言

诊断试验是指为受试者做出诊断所应用的各种实验室检查、影像设备检查、医生的主观诊断以及其他诊断方法，如数学模型、计算机辅助诊断程序等。准确的诊断试验能够使患者得到更及时、更准确的治疗。因此，正确而客观地评价诊断试验具有重要的临床意义。评价诊断试验的传统方法是使用灵敏度、特异度、准确率等指标。由于这些指标受主观选定的诊断分界点的影响，所以难以全面反映诊断试验的优劣。

受试者操作特征（Receiver Operating Characteristic，ROC）曲线与诊断分界点无关，能客观、全面地反映诊断方法对疾病的鉴别能力，从而在诊断试验评价中得到越来越广泛的使用[1-2]，目前已成为国内外公认的标准临床筛查与诊断评价统计学方法。生成ROC曲线的方法分为参数法和非参数法。参数法通过数学模型（双正态模型[3]、累积Logit模型[4]、基于贝叶斯估计的ROC 曲线回归模型[5]等）估计和建立ROC曲线，它要求诊断试验数据不应明显偏离正态分布。非参数法[6-8]则是通过试验数据直接产生ROC曲线，它对诊断试验数据没有分布假设，特别是对于连续型诊断试验数据能够生成无偏的ROC曲线[9]。

目前，国外较权威和常用的医学统计软件，如SAS和SPSS均提供了非参数法ROC曲线分析的功能，但它们无法对两个诊断试验进行ROC曲线下面积的比较。可以进行ROC曲线下面积比较的软件，如ROCKIT采用了双正态参数法ROC曲线估计，对于不符合条件的资料可能得到不正确的结果[10]。为此，我们利用Matlab软件编制了非参数法ROC曲线分析软件，它不仅能够生成ROC曲线，还能对两个诊断试验进行比较，并能保存ROC曲线上操作点的坐标以便其他程序调用，其性能优于其他基于Matlab的ROC曲线绘制程序[11]。

1 非参数法ROC曲线分析的基本思想

ROC曲线非参数分析法目前应用最广泛的是Hanley和McNeil法。虽然也有人提出了其他非参数法，但因为其计算复杂，很少有人使用。而Hanley和McNeil法计算相对简单，容易理解，适用于一般的有序分类资料与连续型资料，其基本原理如下。

1.1 灵敏度和特异度

选定某一诊断分解点后，将诊断试验结果与金标准结果比较，可以得到以下诊断试验评价四格表（表1），从而方便地计算灵敏度和特异度指标[10]。

表1 诊断试验评价的四格表

1.2 ROC曲线

将诊断分界点遍历所有可能的值，则得到由原始试验数据对应的一系列灵敏度与特异度。以每一诊断分界点下的1－特异度和灵敏度为横纵坐标生成一个点，称之为操作点。依次连接所有操作点即得到ROC曲线。

1.3 ROC曲线下面积

ROC曲线下面积（Area Under The Curve，AUC）用于定量的评价和比较诊断试验。假设正常组有n例试验数据xni（i=1, 2, …,n），异常组有 m 例试验数据 xmj（j=1, 2, …,m）。根据Wilcoxon Mann-Whitney统计量，AUC等于异常组每个试验数据＞正常组每个试验数据的概率[4]，即：

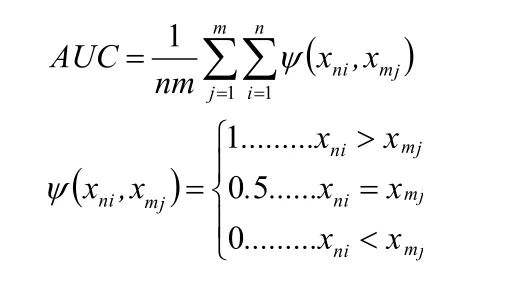
AUC的标准为：

其中，Q1是任意随机选择两个异常组的试验数据都将大于任意随机选择的一个正常组的试验数据的概率，Q2是任意随机选择一个异常组的试验数据都将大于任意随机选择的两个正常组的试验数据的概率。

当有两个针对同一组对象的诊断试验时，可以对两个诊断试验的AUC进行u检验，从而确定两个诊断试验差异的统计学意义。u检验的计算公式为[7]：

其中，r为两个诊断试验得到的AUC的相关系数，通过查表2得到。

在文献[7]中，两个诊断试验ROC曲线下面积的相关系数表中并不包含表2中阴影部分的数字，即原文对于异常组和正常组诊断结果的平均相关系数最大为0.90。而在实际应用时，有可能出现平均相关系数＞0.90的情况。因此，我们对原文中某一平均面积下诊断结果平均相关系数与AUC的相关系数进行二次拟合（拟合方程的决定系数R2>0.999），并推算诊断结果平均相关系数为0.92～1.00时对应的AUC相关系数，即得到表2中阴影部分的数字。

2 基于Matlab的ROC曲线分析软件

根据上述原理，我们利用Matlab软件编写程序，并设计出图形用户界面。

2.1 软件功能

2.1.1 数据输入

软件提供了两种输入诊断评价数据的方法。用户既可以直接从键盘录入数据，也可以导入事先保存好的Excel数据文件。需要注意的是输入和读入的数据一定要与选择的诊断试验个数一致。数据的类型可以是有序分类型数据（等级资料），也可以是连续型数据。

2.1.2 ROC曲线分析

对单个诊断试验，使用原始数据绘制ROC曲线，并利用非参数方法计算ROC曲线的AUC及该AUC与毫无诊断能力的AUC=0.5进行比较P值。

对于两个配对设计的诊断试验，使用原始数据绘制两条ROC曲线，并利用非参数方法计算AUC并比较，给出AUC的值和检验统计量u及P值。

2.1.3 保存结果

软件给出了ROC曲线中每个操作点的坐标值，即1-特异度和灵敏度。这些数据可以导出为Excel工作簿文件，供其他软件调用和分析，如绘制更美观的ROC曲线，计算最佳诊断分界点等。

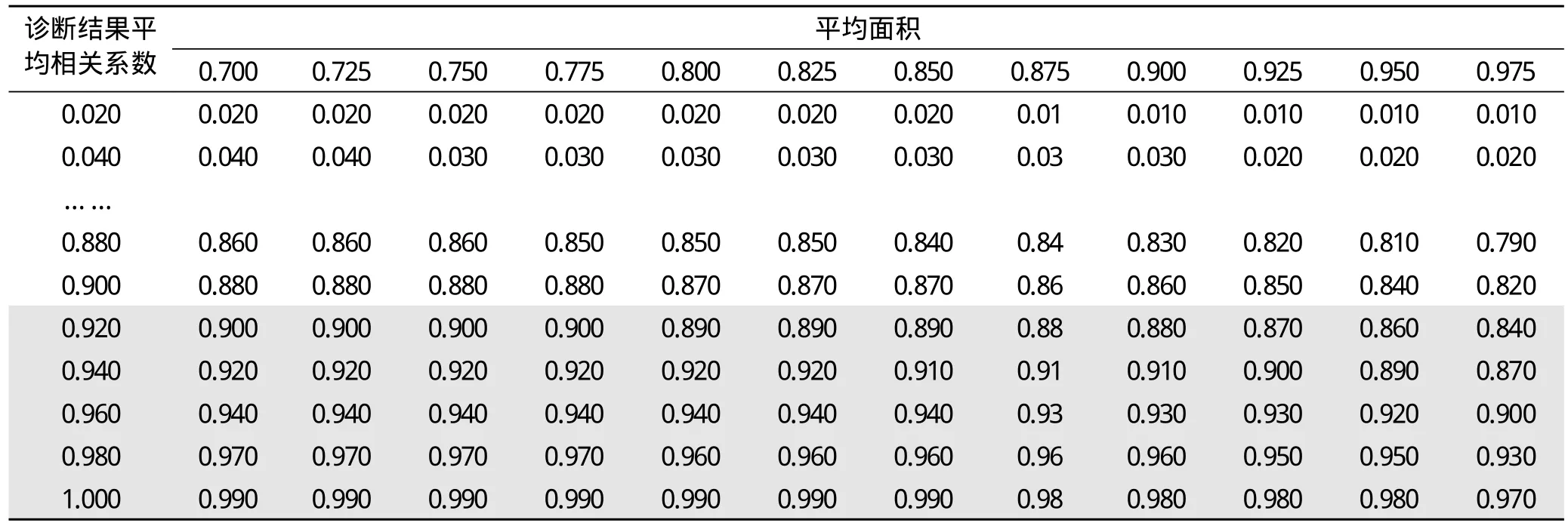
表2 两个ROC曲线下面积的相关系数[7]

2.2 软件验证

我们以文献[6,8]的数据为例，分别用本软件、SPSS以及Analyse-it（Analyse-it Software Ltd., http://www.analyse-it.com/）进行单个及两个诊断试验的非参数法ROC曲线分析，结果见表3～4。

表3 对文献[6]中数据的分析结果

表4 对文献[8]中数据的分析结果（AUC±SEAUC）

3 应用实例

现用A、B两种技术检测45例患者（其中21例确诊患有洛矶山斑疹热洛矶山斑疹热（RMSF），24例为普通发热）的血清钠水平，想了解血清钠水平对RMSF是否有诊断作用，以及哪种检测技术更准确。数据来源于GehlBach（1988年），数据散点图，见图1。

从图1可以看出，两种技术检测得到的血清钠水平都不能将RMSF患者与普通发热患者完全分开，且两种检测结果的区分度不同，方法1稍好于方法2。将原始数据保存为.xls格式文档，在本软件中导入数据后的结果，见图2。

图1 实例数据的分布散点图

图2 软件运行实例的结果

图2左下方为导入的原始数据，右上方为两种技术检测血清钠水平对RMSF进行诊断对应的ROC曲线。两种方法检测结果诊断的ROC曲线下面积分别为0.8750±0.0507和0.8080±0.0644，均在0.7～0.9的范围内，说明血清钠水平对RMSF具有中等程度的诊断作用。

对两条曲线下面积进行比较，u=3.183，P=0.0015，说明两种检测技术诊断RMSF的准确度确有差异，实线ROC曲线对应的方法1更准确。该结果与图1的直观反映完全吻合。

4 讨论

传统的诊断试验评价指标包括正确率、灵敏度、特异度、约登指数、阳性/阴性预测值等。这些评价指标的共同不足是评价结果随着诊断分界点选取的不同而改变，且易受到发病率的影响。ROC曲线综合了特异度和灵敏度两个指标，摆脱了患病率对评价结果的影响，特别是考虑到了所有可能的诊断分界点，曲线下面积还能够用来对诊断试验进行定量的评价和比较，从而成为公认的最佳诊断试验评价工具。在本文的应用实例中，两种血清钠水平检测方法所得结果的ROC曲线下面积分别为0.875和0.808，说明两种方法测得的血清钠水平均具有一定的诊断能力。对两种检测结果的诊断价值进行比较，得出P<0.05，即两条曲线的曲线下面积之差为0.067，差异有统计学意义，方法1检测得到的血清钠水平诊RMSF的准确性更高。

ROC曲线分析分为参数法和非参数法。一般认为非参数法因其没有条件限制，所以可以应用于所有诊断试验的准确度评价，但计算的ROC曲线下面积往往偏小；而参数法可较准确地估计ROC曲线下面积，但在样本量较小或资料远远偏离其应用条件（服从双正态分布）时，估计的结果可能严重偏离真实值；在样本量较大且相同值较少时，参数法和非参数法估计的ROC曲线下面积则近似相等。因此，在实践中，样本量大时可选择参数法或非参数法估计ROC曲线下面积，样本量较小时选择非参数法[13]。

由于目前较为权威的医学统计软件SPSS和SAS都只提供了非参数法计算ROC曲线下面积的功能，而不能对曲线下面积进行比较，为此，我们利用Matlab的图形用户界面编写了具有导入、保存、图形展示等功能的非参数法ROC曲线分析软件，并补充了经典文献提供的ROC曲线下面积相关系数表。本软件具有计算准确、通用性强、界面友好、操作简便、结果简洁等特点，在实际工作中具有一定的实用价值。

[1]王忠周,张经建,王新怡,等.应用ROC曲线对比研究数字乳腺机不同靶面/滤过组合的辐射剂量及图像质量[J].医学影像学杂志,2011,21(3):429-432.

[2]张瑞,郑玄中,靳宏星,等.应用ROC曲线评价DWI诊断直肠癌的价值[J].实用医学影像杂志,2011,12(3):170-173.

[3]Charles E Metz.ROC analysis in medical imaging:a tutorial review of the literature[J].Radiological Physics and Technology,2008, 1(1):2-12.

[4]宇传华,余松林,徐勇勇.比例优势模型实现ROC分析的方法及其应用前景分析[J].中国卫生统计,2005,22(5):293-296.

[5]尉洁,宋娇娇,赵晋芳,等.基于贝叶斯估计的诊断试验ROC曲线回归模型[J].中国卫生统计,2010,27(2):152-154.

[6]Hanley JA,McNeil BJ.The meaning and use of the area under a receiver operating characteristic (ROC) curve [J].Radiology,1982,143:29-36.

[7]Hanley JA,McNeil BJ.A method of comparing the areas under a receiver operating characteristic curves derived from the same cases [J].Radiology,1983,148: 839-843.

[8]DeLong ER,DeLong DM,Clarke-Pearson DL.Comparing the areas under two or more correlated receiver operating characteristic curves:a nonparametric approach [J].Biometrics,1988,44:837-844.

[9]Kelly H Z,A James O' Malley,Laura M.Receiver-operating characteristic analysis for evaluating diagnostic tests and predictive models[J].Circulation,2007,115:654-657.

[10]Stephan C,Wesseling S,Schink T,et al.Comparison of eight computer programs for receiver-operating characteristic analysis[J].Clinical Chemistry,2003,49(3):433-439.

[11]石昊苏.基于实例与MATLAB的ROC曲线绘制比较研究[J].电子设计工程,2010,18(9):36-39.

[12]宇传华.ROC分析方法及其在医学研究中的应用[D].西安:第四军医大学,2000.

[13]宋花玲,贺佳孙,黄品贤,等.ROC曲线下面积估计的参数法与非参数法的应用研究[J].上海:第二军医大学学报,2006,27(7):726-728.