滑坡体监测数据的改进变维分形－人工神经网络耦合预测模型

秦 鹏，张喆瑜，秦植海，王维汉

(1.浙江水利水电专科学校，杭州 310018;2.水利部农村电气化研究所，杭州 310012;3.河海大学水文水资源与水利工程科学国家重点实验室，南京 210098)

1 研究背景

滑坡是一种造成重大人身及财产损失的自然灾害现象，随着我国位于高山峡谷地区的大型工程项目的日益增加，滑坡的危害日益突出［1］。由于岩土体是一种非均质各向异性且具有流变特性的复杂介质，加之地质条件的复杂性，使得其力学参数和演化特征具有很强的随机性和不确定性，从而导致滑坡动态信息极难捕捉，加之动态监测技术的不成熟和预报理论的不完善，滑坡变形预测一直是边坡工程中的主要难题之一［2－3］。

目前用于滑坡监测资料时间序列预测的建模方法主要有时间序列分析法和智能岩石力学方法，如多项式回归、灰色系统分析模型、混沌理论等［4］，但是这些方法都对数据的长度有较强的依赖性，监测数据量较少以及数据中白噪的干扰都会对这些方法的预测精度造成较大影响，当滑坡体监测数据较短或存在残缺时，预测效果并不理想［4－5］。分形理论基于部分与整体的自相似性，直接从非线性复杂系统的本身入手，分析研究对象的自身性质和规律，能够揭示隐藏于混乱复杂现象中的精细结构和定量地描述系统，为岩质滑坡体的监测数据时间序列的预测提供了新的途径［6］。

在过去的研究中，笔者利用分形理论对岩质边坡进行了分形特征分析，发现高陡边坡可以看作一个具有自相似性的复杂非线性系统，分形维数可以从整体上描述边坡安全监控数据的动态变化特征［7－8］。并尝试运用改进变维分形(Improved Variable Dimension Fractal，IVDF)模型建立边坡数据分形动力模型，对小数据量的边坡监测数据进行预测，IVDF预测模型充分利用分形理论的自相似性特征，具有较强的抗噪性，对小数据量监测数据具有较好的预测效果，但也存在预测时间较短、人为因素干扰大的缺点［9］。作为后续研究，本文引入具有较强自我学习能力的人工神经网络模型(Artificial Neural Network，ANN)对分形预测模型预测结果进行优化，提出了改进变维分形－人工神经网络(Improved Variable Dimension Fractal-Artificial Neural Network，IVDF-ANN)耦合预测模型，并以茅坪滑坡的位移监测序列为例，进行了实例研究。

2 改进变维分形-人工神经网络(IVDF-ANN)耦合预测模型的建立

2.1 分形理论及改进变维分形模型的建立

分形理论是美籍法国数学家B.B.Mandelbor所创立的一种全新意义上的数学结构分析方法，其研究对象为自然界和社会活动中广泛存在的无序(无规律)而具有自相似性的系统［10］。已有的研究表明，在越混乱、越无规则、越复杂的领域，用分形理论处理问题一反常态就越有成效［11］。目前常用的分形模型主要有常维分形和变维分形2种，具体定义可查阅文献［6，11］。由于自然界中严格意义上满足常维分形的现象是不存在的，所以大量数值模型需要用变维分形的方法进行计算，但当数据复杂时，变维分形中的函数式又往往庞大而难于计算［9］。研究证明，对于任意函数关系N=f(r)都可以转换成常维分形N=C/rD的形式，即将数据进行一系列的变换，使变换后的数据能用常维分形处理，即通过构造1阶、2阶、3阶……累积和的分段变维分形模型，然后选择效果最好的变换并确定相应的分形参数［12］，改进变维分形模型的具体预测步骤如下。

(1)将监测数据点(Ni，ri)(i=1，2，…，n)绘于双对数坐标上，将Ni排成一个基本序列，即

(2)根据基本序列构造累积和序列。例如构造一节累积和序列 S1，其中 S11=N1，S12=N1+N2，S13=N1+N2+N3，…，同样可以构造二阶、三阶累积和等，即:

(3)建立各阶累积和的变维分形模型。以一阶累积和为例，利用常维分形维数D=ln(Ni/Nj)/ln(rj/ri)计算数据点(S1i，ri)和(S1i+1，ri+1)，在双对数坐标中的斜率的相反数D1i，i+1，即一阶累积和的分段变维分形的分维数。根据n个数据对，可以得到的是n－1段分段变维分形的维数，称之为分维数序列［6，12］。用 DNi，i+1表示 N 阶累积和的分段变维分形的分维数序列，N=1，2，…;(i=1，2，…，n－1)。

(4)选择最好的变换并确定相应的分形维数。比较各阶分段变维模型，并选择效果最好的变换，按照上述步骤确定分形维数。并选择一条效果最好的分维数序列曲线，拟合计算出分形参数。

(5)根据选定的分形维数带入改进变维分形模型，可对监测数据时间序列趋势项进行预测。

2.2 神经网络预测模型

BP网络人工神经网络中的一种，它通过将网络输出误差反馈回传来对网络参数进行修正，从而实现网络的映射能力。理论上已经证明，单隐层BP网络，只要神经元数量足够多，可以精确逼进任何复杂的曲面和多维欧氏空间曲面［13］，通过试算也证明隐含层只取一层即可满足拟合精度要求。BP网络的具体算法可参见相关文献［14］。

在BP网络建模过程中要注意以下3个问题。

(1)数据预处理。为便于预测，对偏离项进行归一化处理，归一化公式如下:

(2)滚动学习。根据预测理论，随着预测步数的增大，误差急剧增大，为了充分利用最新的监测信息，提高预测的准确性，采用滚动预测的方法，该方法又称为实时跟踪算法(Realtime Tracing Algorithm)［15］。基于此思想，对BP网络的偏离项学习、预测方法进行如下设定:

设置输入数据为V(k)=［v(k)，v(k+1)，…，v(k+m－1)］，k=1，2，…，n;输出数据为v(k+m)，k=1，2，…，n;即以数据的前m个偏离量作为学习样本，第m+1个偏离量作为输出样本，学习完成后，把输出样本加入学习样本并剔除原学习样本中的第一个偏离量……通过已知偏离项数据的“新陈代谢”，加强网络的自我学习能力，使实时跟踪学习成为可能，提高了模型对偏离项的外推泛化能力。网络结构图1如所示。

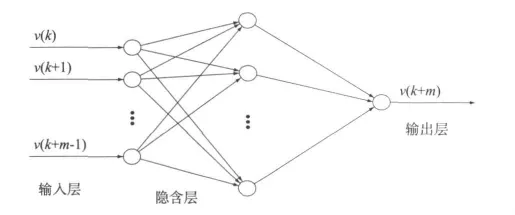
图1 网络结构示意图Fig.1 Typical structure of feedforward ANN

(3)网络结构改进。对于单隐含层BP神经网络，理论上只要隐含层节点数量足够多，就可以逼近任何复杂的非线性映射，这固然是优势所在，但同时也带来映射能力过剩、网络不易收敛的问题［14－15］。因此采用有动量的梯度下降法对BP网络进行改进:

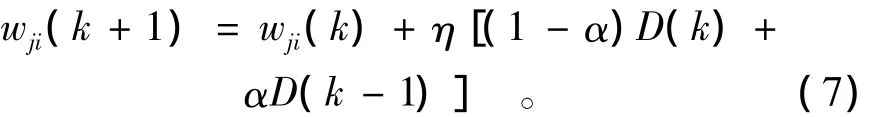
式中:D(k)表示k时刻的负梯度;D(k－1)表示k－1时刻的负梯度;η为学习率;α∈［0，1］是动量因子。方法中所加入的动量项在实际效果上相等于阻尼项，它减小了学习过程的振荡趋势，从而改善了收敛性，提高了网络对偏离项的预测精度［14］。

2.3 改进变维分形-人工神经网络模型的建立方法

作为系统内部变化趋势的外在表象，滑坡体监测非线性时间序列在普遍情况下包含趋势项，即非平稳的时间序列［1－2］。本文在监测数据趋势项的基础上提出偏离项的概念，即用R表示时间序列监测数据，将时间序列监测值分解为

式中:U表示时间序列的趋势项;V表示时间序列的偏离项。

改进变维分形－人工神经网络耦合预测模型的建模思路是:首先对原始监测数据进行分形特征分析(分析方法可参见相关文献［7，9－10］)，如果监测序列具有分形特征，则用改进变维分形模型对原始监测数据进行拟合，得到趋势项;通过神经网络对于偏离项进行多次自我学习，训练精度较高的网络模型，进而对偏离项进行预测;将趋势项与由神经网络模型得到的偏离项外推数据进行叠加，即可得到更高的预测长度与精度。对于非线性的监测数据，分形模型能较好地拟合出时间序列的趋势项，构成了预测主体，而利用人工神经网络的自学能力对数据偏离项进行外推预测，是对趋势项的一次修正，减少了人为因素的干扰，进一步提高了预测的精度，延长了预测时间。建模流程如图2所示。

3 实例研究

为验证上节提出的IVDF-ANN模型预测的有效性，这里以文献［16］中给出的茅坪滑坡的位移监测序列为例进行说明。

茅坪滑坡体位于清江隔河岩水利枢纽库区中上段左岸，是清江库区规模最大的滑坡体。茅坪滑坡体是一个具有多级、多期次滑动特征的古滑坡体，平面上呈帚状形态，长轴方向近SN向，自从1993年4月10日隔河岩水库大坝下闸蓄水以来，茅坪滑坡体发生明显位移，并且具有显著增长趋势。因此，该滑坡体的稳定性及在未来一段时期内的位移发展趋势成为人们十分关注的问题［16］。

图2 IVDF-ANN耦合预测模型建模流程图Fig.2 Flow chart of IVDF-ANN coupling model construction

本文选取1993－1995年3年间的4#观测点25个位移监测数据作为样本，建立监测数据的时间序列，采用本文提出的IVDF－ANN耦合预测模型对位移监测数据进行尝试性研究。模型选取前15个监测数据作为计算数据，后10个数据用以检验，为方便计算，以监测数据的时间先后进行编号，r=1，2，…。

文献证实，岩质高边坡是一个非线性动力系统，监测时间序列具有分形特征［7］，故可以用 IVDFANN模型进行预测、分析。首先，通过改进变维分形模型提取监测数据时间序列的趋势项。对监测数据进行1～4阶累积和序列的构造，分别求出4#测点监测值的各阶分维值，如表1所示。

表1 茅坪滑坡体4#测点趋势项变维分形维数计算结果Table 1 Result of n-order variable-dimensional fractal sequences at Maoping landside monitoring point 4#

为了便于直观的分析和选取，将表1数据绘制于图3，可以看到D2，D3系列值拟合效果都比较理想，特别是D2曲线在后半段十分平顺。因此，本文选取D2曲线作为预测模型的分形参数曲线，对曲线的分段分形维数进行拟合、反推，得到模型的趋势项序列如表2所示。

图3 茅坪滑坡体4#测点趋势项各阶变维分形维数汇总Fig.3 N-order variable-dimensional fractal sequences at Maoping landside monitoring point 4#

由于二阶分形维数曲线的前端有较大变化，造成模型的趋势项拟合前端不是十分理想，故趋势项从序列5开始统计，由边坡位移的实际监测序列和趋势项序列，可以得到模型的偏离项。偏离项时间序列的符号不定，因此对序列进行归一化处理，可得偏离项网络训练值，把它列入表2。

设定偏离项BP神经网络输入层为5个节点，输出层为1个节点，根据Kolmogorov定理，设定隐层的节点数为15，训练精度设定为0.001，动量因子数为0.9，采用动量梯度下降法对偏离项训练值进行滚动学习。验证表明，网络输出值与期望值很接近，证明训练后的BP网络已较好掌握输入与输出间的映射关系。动量梯度法训练过程如图4所示。

图4 偏离项BP神经网络训练过程线Fig.4 BP-ANN training performance of deviation items

表2 茅坪滑坡体改进变维分形-神经网络预测表Table 2 Results of displacement prediction for Maoping landside by IVDF-ANN model mm

对于训练好的网络，以预测值补充到输入项中并及时剔除原始数据的实时跟踪算法，对边坡位移偏离项进行滚动预测。得到的监测数据偏离项预测值经还原后与趋势项叠加即可得到位移的预测值，见表2。

由表2可见，本文模型所得到的位移预测值同实测值比较接近，为了直观的反映模型的预测效果，图5给出了本文的预测值与实际边坡位移监测值的比较曲线，可以看到预测曲线在较好拟合位移变形趋势的基础上，保持了较强的外推预测能力和较高的精度，说明改进变维分形－人工神经网络(IVDFANN)模型较好地揭示了滑坡体的非线性演变规律，可以较有效地应用于滑坡的监测数据预测研究。

图5 茅坪滑坡体位移预测值与实际监测值的比较曲线Fig.5 Comparison between measured and predicted displacements at Maoping landside

4 结论

在分形理论的基础上，尝试改进变维分形模型和人工神经网络(IVDF－ANN)耦合预测模型，并应用此模型进行茅坪滑坡体4#观测孔的位移预测，计算结果显示，该模型发挥分形理论自相似性的特点和人工神经网络自我学习的能力，充分挖掘小数据量监测数据本身的非线性动态信息，具有良好的抗噪性，能够达到较高的预测精度和较好的预测长度。本文的进一步工作是通过对多个边坡的变形实际计算，证明预测模型的通用性，另外，进一步增加预测时间、提高预测精度也是模型需要改进和探讨之处。

［1］黄润秋.20世纪以来中国的大型滑坡及其发生机制［J］.岩石力学与工程学报，2007，27(3):433－454.(HUANG Run-qiu.Large-Scale Landslides and Their Sliding Mechanisms in China Since the 20th Century［J］.Chinese Journal of Rock Mechanics and Engineering，2007，27(3):433－454.(in Chinese))

［2］王思敬.论岩石的地质本质性及其岩石力学演绎［J］.岩石力学与工程学报，2009，28(3):433－450.(WANG Si-jing.Geological Nature of Rock and Its Deduction for Rock Mechanics［J］.Chinese Journal of Rock Mechanics and Engineering，2009，28(3):433－450.(in Chinese))

［3］秦植海，秦 鹏.高边坡稳定性评价的模糊层次与集对分析耦合模型［J］.岩土工程学报，2010，32(5):706－711.(QIN Zhi-hai，QIN Peng.Evaluation of Coupling Model’s High Slope Stability Based on Fuzzy Analytical Hierarchy Process-Set Pair Analysis Method［J］.Chinese Journal of Geotechnical Engineering，2010，32(5):706－711.(in Chinese))

［4］林鲁生，刘祖德.人工神经网络在边坡滑移预测中的应用［J］.岩土力学，2002，23(4):508－510.(LIN Lusheng，LIU Zu-de.Application of Artificial Neural Network to Prediction of Sliding Slope［J］.Rock and Soil Mechanics，2002，23(4):508－510.(in Chinese))

［5］秦 鹏.基于非线性理论的高边坡监测数据分析与预测［D］.合肥:合肥工业大学，2009.(QIN Peng.Analysis and Prediction of High-slope Model’s Monitoring Data Based on Nonlinear Method［D］.Hefei:Hefei University of Technology，2009.(in Chinese))

［6］MANDELBROT B B.Les Objets Fractals:Forme，Hasard et Dimension［M］.Paris:Flammarion，1975.

［7］秦 鹏，秦植海.基于分形理论的岩质高边坡监测资料分析［J］.水利水运工程学报，2008，9(3):92－97.(QIN Peng，QIN Zhi-hai.Analysis of High Rocky Slope Monitoring Data Based on Fractal Theory［J］.Hydro-Science and Engineering，2008，9(3):92－97.(in Chinese))

［8］秦 鹏，秦植海.压实填土随浸水时间增长强度降低规律研究［J］.浙江水利水电专科学校学报，2010，22(2):61－64.(QIN Peng，QIN Zhi-hai.Study on the Law Between Soaking Time and Strength of Compacted Filling Earth［J］.Journal of Zhejiang Water Conservancy and Hydropower College，2010，22(2):61－64.(in Chinese))

［9］秦 鹏，秦植海.岩质高边坡监测数据的改进变维分形预测模型［J］.水利水运工程学报，2010，3(1):90－94.(QIN Peng，QIN Zhi-hai.Forecasting Model of Monitoring Data of Rock High Slope Based on Improved Variable Dimension Fractal Theory［J］.Hydro-Science and Engineering，2010，3(1):90－94.(in Chinese))

［10］HURST H E.Long-Term Storage in Reservoirs:An Experimental Study［J］.Transactions of the American Society of Civil Engineers，1951，116(4):770－808.

［11］MANDELBROT B B，EVERTSZ C J G，JONES P W.Fractals and Chaos:The Mandelbrot Set and Beyond［M］.New York:Springer，2004.

［12］付昱华.变换形成的分形与海洋环境数据分析预测［J］.海洋通报，2000，19(1):79－88.(FU Yu-hua.Transform-Formed Fractals and Analyses and Forecast of Marine Environment Data［J］.Marine Science Bulliten，2000，19(1):79－88.(in Chinese))

［13］HAYKIN S S.Kalman Filtering and Neural Networks［M］.New York:John Wiley and Sons，Inc.，2004.

［14］HAYKIN S S.Neural Networks and Learning Machines［M］.New Jersy:Prentice Hall，2008.

［15］TIAN H，PASCAL VICAIRE，TING YAN，et al.Achieving Real-Time Target Tracking Using Wireless Sensor Networks［C］∥Institute of Electrical and Electronics En-gineers.Proceedings of the 12th IEEE Real-Time and Embedded Technology and Applications Symposium，San Jose，California，April 4－6，2006:37－48.

［16］吴益平，滕伟福，李亚伟.灰色-神经网络模型在滑坡变形预测中的应用［J］.岩石力学与工程学报，2007，26(3):632－636.(WU Yi-ping，TENG Wei-fu，LI Yawei.Application of Grey-Neural Network Model to Landslide Deformation Prediction［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26(3):632－636.(in Chinese))