基于GGASA算法优化信号互相关的MIMO雷达波束形成技术
张 杰
(南京电子技术研究所,南京 210039)
0 引言
传统相控阵的特点是高增益、定向性波束,适合于跟踪和小区域搜索。这种体制特别适合于目标方位已知的情况,例如跟踪状态,或较窄空域的搜索等。但未来雷达系统的特征要求在确保雷达发射全功率的条件下,可以采用新的技术实现在线自适应发射波束的合成[1~4]。
与之相对应地,MIMO雷达系统采用互不相关的波形,能够形成宽开的空间方向图,即全方向的或更实际的单个发射子孔径的波束方向图。相关研究表明通过具有任意互相关特性的信号集合的选择能够综合波束方向图。通过信号互相关矩阵的设计,可以构造不同的空间波束形状,包括相控阵系统的高增益定向性波束和采用正交信号MIMO系统的全方向性波束等。该设计途径一种有益的应用就是在线或联机地选择或修正雷达天线的空间波束方向图,以获得在跟踪方式下的目标精确定位。
众所周知,常规雷达为了充分利用辐射功率多采用恒包络信号。对于全相干信号,降低波束旁瓣电平和获得波束展宽的唯一方法就是对单元进行加权处理,这种方法会有一定的发射功率损失。文献[4]提到如果能够利用控制信号的互相关来进行波束方向图的合成则可以在各种情况下充分利用信号的发射功率。此外,这种情况下波束综合也会有更多的自由度供设计选择,如N(N-1)/2信号互相关参数相对于N个信号相位或抽头延迟线权值将有很大的灵活性。
通过互相关设计波束图是一个新的领域,很难用显式直接表达其结果。文献[4]提出了将波束综合问题表述为在正定Hermitian矩阵构造的S+空间上的受限优化问题,并用两个关系式对该问题进行了表示。本文在计算方法上开展了工作,引入全局遗传模拟退火算法(GGASA,global genetic simulated annealing algorithm)对波束综合问题进行最优化搜索,获得了较好的结果。
1 MIMO雷达的概念
作为一种全新的体制,MIMO雷达借鉴了在通信领域取得巨大成功的多输入多输出概念,初步的研究已显示该体制对于提高雷达性能的显著作用。不同于传统的实现最大化相干处理增益的阵列天线雷达系统(radar array system),MIMO雷达利用目标的散射特性实现分集处理,改善雷达的性能,如图1所示[2]。
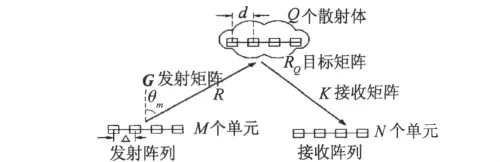
图1MIMO雷达示意图
在传统的雷达中,目标的闪烁被认为是有害的现象,产生的雷达散射截面(RCS,radar cross section)起伏会降低雷达的性能。理论和试验都证实,目标相对于雷达距离和方位的微小变化都可能引起回波能量的剧烈起伏,即使是千分之一弧度角的方位变化都可能导致回波能量产生10 dB以上的闪烁起伏。目标回波的这种起伏引起了信号衰落,造成系统性能的急剧下降。RCS动态起伏引起目标散射截面积的变化是随机的,可以应用随机过程对其进行统计建模,包括:Swerling I、II、III和IV四类模型,有时也将RCS恒常不变的目标看作Swerling V型。
由Swerling模型描述的雷达回波信号起伏剧烈,导致了探测性能的下降;克服该问题的一种方法是通过采用阵元间隔很近的系统最大化相干处理的增益;另一种方法就是采用分集技术,频率分集、极化分集或者空间分集(码元分集)。其中,空间分集也就是MIMO雷达,其独特性就在于它从相反的方向考虑问题,利用目标的闪烁效应改善雷达性能;并且通常空间分集获得的增益大于相干处理的结果[1~3]。
接收机高度相关的阵列信号可以实现雷达的相干处理,而MIMO雷达接收的阵列信号是互不相干的,可以将探测器输出进行非相干的组合,使得接收的衰落信号相互对立地进行叠加,平均SNR保持基本恒定,达到了克服回波信号起伏的问题。这是与传统雷达显著不同的一点。通过将雷达天线的发射和接收阵元间隔一定的距离以使得目标的角散射更加明显;同时考虑到探测目标的复杂形状,以及与天线阵元之间的距离等因素,每个阵元都能观测到目标不同的侧面,MIMO雷达应用目标散射源的空间分集特性为改善雷达的性能开辟了广阔的技术思路。
2 MIMO波束优化形成
2.1 基本原理
设一组天线阵元模块构成的线阵天线及所处的坐标系统如图2所示[4]。
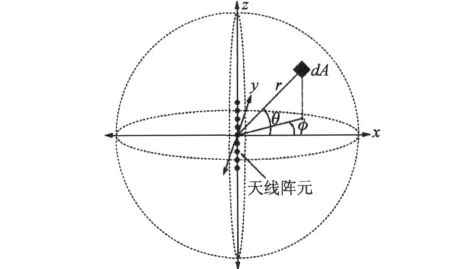
图2 线阵天线的阵元及所处的坐标系统
设每个模块的输入信号为si(t),i=1…N。在不考虑系统损耗的理想情况下,每个组件辐射的平均功率为

上划线表示取平均。
信号si(t)在距离为r的远场输出为

式中,k表示(θ,φ)方向的单位向量。
发射的功率密度可表示为
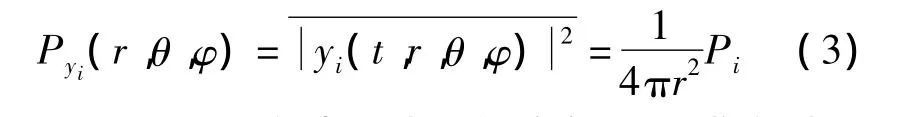
即Pyi(r,θ,φ)在半径为r的空间积分求和就可得到总的发射功率Pi。
考虑各个发射信号在空间的功率合成,可得

相应地,总的功率密度为
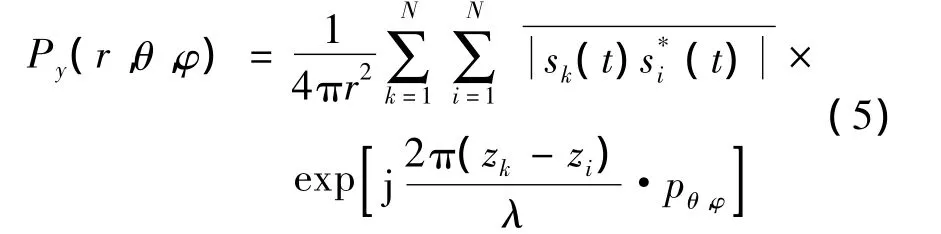
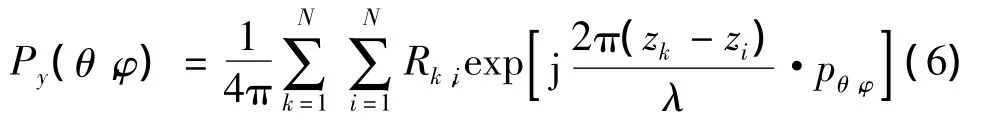
设 ψi(θ,φ)=(2πzi)/λ·pθ,φ,方向矢量可表示为
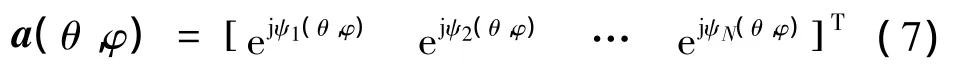
由此,式(6)可表示为
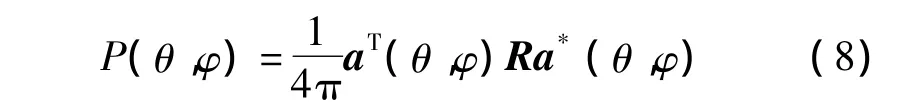
归一化的功率密度P(θ,φ)即为希望通过信号参数的处理来综合的功率方向图。该通用的表达式,既包括了相控阵的情况,即R秩为1{P(θ,φ)=[aT(θ,φ)a*(θ,φ)]/4π};也包括了发射信号互不相关的MIMO的情况,即R为多重的单位矩阵I。通过灵活选择雷达发射的信号si(t)构造合适的R可以获得需要的辐射方向图。
由此可见,通过选择最优的相关矩阵R可获得需要的空间辐射波束方向图。随之而来的问题就是如何选择合适的矩阵R来得到期望的方向图。从数学角度看,这就是一个受限的最优化求解问题。
2.2 基于GGASA的优化搜索算法
遗传算法(GA)是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法,其主要特点是群体搜索策略和群体中个体之间的信息交换,搜索不依赖于梯度信息。选择、交叉和变异是遗传算法的主要操作算子。虽然GA有较强的全局搜索性能,但存在局部搜索能力较差和收敛过早等问题。模拟退火(SA)法是一种基于热力学的退火原理建立的随机搜索算法,具有很好的局部搜索能力,而且也是一种以概率1收敛于全局最有解的全局优化算法,但其相关参数的选取对搜索性能有很大的影响。全局遗传模拟退火算法是将GA和SA算法相结合而构成的一种优化算法,其原理流程如图3所示。
参照雷达的工程实际情况,R有两个限定条件,即:R必须为正定矩阵和每个辐射单元必须工作在饱和状态所限定的矩阵R,即
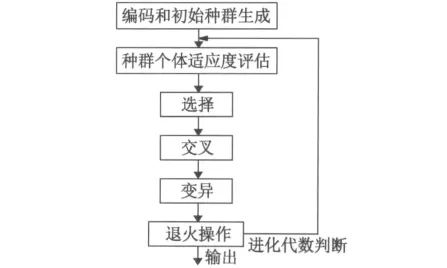
图3GGASA算法流程图

不失一般性,可设¯P=1,则相关矩阵R的对角元素 rii=1(i=1,…,N)。
非负正定矩阵的空间边界是一个复杂的曲面,造成这种非负限制很难直接求解。为了规避这个问题,文献[4]中将矩阵R进行了Cholesky因子表示,即

这样问题的求解就转换成了在Cholesky因子所在的空间L上搜索。
在L空间搜索保证了R的正定特征。R的对角线上的元素rii=lilHi,li为L的第i行。在功率受限的条件下,即¯P=1,可以转换为
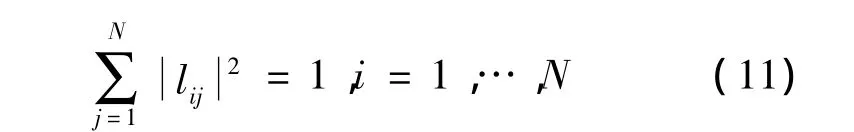
li是(i-1)维复球面上的行向量。完整的搜索空间为所有这样的复球面构成的乘积空间CS0×CS1× … ×CS(N-1)。
下述内容为采用GGASA算法综合设计产生设定MIMO雷达波束发射信号的主要步骤。
(1)生成初始种群
设阵元个数N=19,种群个数M=100。通过随机方法生成初始种群,记为 P0=[X01,X02,…,X0M];并设计产生的方法使得种群个体满足功率受限的条件,其中xij为初始种群个体X0k的元素。个体 Xk,(k=1,…,M)表征了L子空间中的元素。
同时,设定SA算法的初始温度T=T0,退火因子α(0<α<1)。
(2)计算适应度函数
波束形成的原则就是尽可能逼近目标波束函数。设目标波束为Pd(θ),可构造适应度函数为
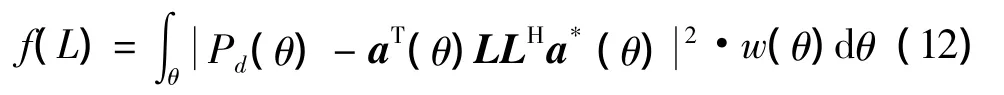
式中,w(θ)表示对目标波束随θ区域变化而进行的差异化加权处理。
(3)精英(Elite)保留策略
将每代群体中的个体的适应度排序,选择出适应度最优的数个(如2)个体,作为种群的精英,直接进入下一代遗传。这种策略确保每个进化代中最优个体的适应度是一个单调的过程,是一个自动寻找最优的过程。
(4)选择
对每代中除精英以外的个体采取轮盘赌选择方法。设除去种群中的精英外,剩余种群中个体数为Q,其中个体i的适应度值为fi,则i被选中的概率为Psi=显然,个体适应度越大被选中的概率就越高。
(5)交叉
对种群中的Q个个体进行单点交叉,即在染色体中随机的设定一个基因位为交叉点,实行交叉时,该点以后的两个个体的部分结构进行互换,并生成两个新个体。
(6)变异
(7)退火操作
(8)更新种群
将Q个经过选择、交叉、变异以后产生的新个体,与直接选择的精英一起构成下一代的种群,同时更新温度参数T=αT,0<α<1,进入下一代的循环操作。
3 仿真结果
设模拟仿真的天线为均匀线性阵列,单元数为19个,单元间距为半波长λ/2。首先设定要产生的波束以阵列侧面为中心的均匀辐射方向图,如图4(虚线)所示。
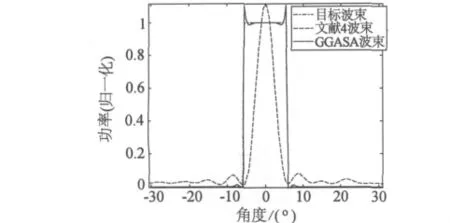
图4 算法综合的波束图
通过GGASA算法优化搜索300代后的综合波束如图4中实线所示,基本可以拟合设定的目标波束图,表明了算法优化搜索任意互相关函数来实现波束成形的可行性。
4 结语
本文通过全局遗传模拟退火算法对MIMO雷达的波束综合问题进行了最优化搜索,获得了初步的结果。下一步的工作可以在优化搜索算法和更新代价函数等途径以获得更优的MIMO雷达波束综合;此外,每个阵元辐射恒包络信号也是工程应用中必须考虑的实际问题,可以在优化求解中作为一项附加条件予以约束,以得到更符合实际情况的MIMO雷达信号。
[1]RABIDEAU D J,PARKER P.Ubiquitous MIMO Multifunction Digital Array Radar[C].The Thirty-Seventh Asilomar Conference on Signals,Systems and Computers,2004,1 057-1 064.
[2]FISHLER E,HAIMOVICH A,BLUM R,et al.MIMO Radar:An Idea Whose Time Has Come[C].The IEEE Int.Conf.on Radar.Philadelphia,PA,2004.
[3]FISHLER E,Haimowich A,BLUM R,et al.Statistical MIMO radar[C].12th Conf.on Adaptive Sensor Array Processing,2004.
[4]DANIEL R FUHRMANN,GEOFFREY SAN ANTONIO.Transmit Beamforming for MIMO Radar Systems Using Partial Signal Correlation[C].Conference Record of the Thirty-Eighth Asilomar Conference on Signals,Systems and Computers,295-299,2004.
[5]Daniel R Fuhrmann,Geoffrey San Antoniot.Transmit Beamforming for MIMO Radar Systems Using Signal Cross-correlation[J].IEEE Transactions On Aerospace And Electronic Systems,2008,44(1):171-186.
[6]何子述,韩春林,刘波.MIMO雷达概念及其技术特点分析[J].电子学报,2005,33(B12):2 441-2 445.

