基于无线传感器网络的调制识别方法
党月芳,徐启建,张 杰,陈 晓
(1.国防信息学院,武汉 430009;2.中国电子设备系统工程公司研究所,北京 100071)
0 引言
通信信号的调制方式自动识别具有重要意义,它为接收信号进一步的分析处理提供重要依据。在民用领域,信号调制方式自动识别应用于频谱监测中的信号身份确认和干扰确认;在军用领域,信号调制方式自动识别应用于对敌方通信信号的截获、干扰和破坏。目前的自动识别方法大多是集中式处理,由单个节点进行信号的预处理、特征提取和分类识别。无线传感器网络在分布式处理方面具有很大优势,基于无线传感器网络的分布式信号检测、估计、识别受到越来越多的关注。
文献[1,2]提出了传感器网络中基于似然函数的调制识别方法,文献[3]提出了基于特征参数的调制识别方法,文献[4]利用无线传感器网络中相互协作的多个传感器,在传感器开销最小的前提下,依据五种特征参数的组合,利用径向基神经网络分类器对数字通信信号进行识别。文章从传感器网络自身特点出发,由传感器节点提取能显著区分信号调制方式的五个特征,构成特征矢量,将特征矢量发送到中心节点,利用粒子群优化算法(PSO,particle swarm optimizer)对神经网络进行训练优化,得到识别结果[5]。
1 基于无线传感器网络的调制识别系统模型
信号从发送机到接收机的过程中,受到地形或障碍物的影响,会发生反射、绕射、衍射等现象,接收机接收到的信号由不同路径的来波组成,由于不同路径的来波到达时间不同,导致相位不同。不同相位的来波在接收端因反相叠加而造成幅度衰落,这种由多径引起的衰落称为多径衰落。发射机与接收机之间存在障碍物时,由于障碍物阻隔而导致信号幅度大幅衰落,这种衰落称为阴影衰落。由于多径和阴影衰落的影响,使得单节点调制识别存在固有的缺陷。
所采用的基于无线传感器网络的调制识别系统模型[2],如图1 所示。

图1 基于无线传感器网络的调制识别系统模型
分布在一定区域内的无线传感器网络节点接收到调制信号,经过相应的预处理后,提取信号的高阶累积量特征,发送到中心节点,由中心节点中的神经网络进行信号的调制识别。传感器节点接收到的信号可表示为式中,A为载波幅度;an为发送码元序列;g(t)为发送码元波形;θc为载波初始相位;n(t)为高斯白噪声。

2 基于无线传感器网络的信号调制识别流程与算法
首先由传感器节点提取信号的五个特征参数,发送到中心节点。在中心节点,用粒子群优化算法优化神经网络的参数,最后利用训练好的神经网络对样本信号进行分类识别。基于无线传感器网络的信号调制识别流程,如图2所示。

图2 基于无线传感器网络的信号调制识别流程
2.1 特征参数的提取
为方便本文提出方法与决策论方法进行对比,采取最常用于决策论方法的参数,参照文献[6~8],提取能显著区分信号调制方式的五个经典的特征参数,分别为
(1)零中心归一化瞬时幅度之谱密度最大值γmax

式中,Ns为取样点数;acn(i)为零中心归一化瞬时幅度,由下式计算

(2)零中心非弱信号段瞬时相位非线性分量绝对值的标准偏差σap

式中,at是判断弱信号的一个幅度判决门限电平;c是在全部取样数据Ns中属于非弱信号值的个数;φNL(i)是经零中心化处理后瞬时相位的非线性分量,在载波完全同步时,有式中为瞬时相位。
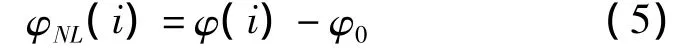
(3)零中心非弱信号段瞬时相位非线性分量的标准偏差σdp

(4)零中心归一化瞬时幅度绝对值的标准偏差σaa为

(5)零中心归一化非弱信号段瞬时频率绝对值的标准偏差σaf
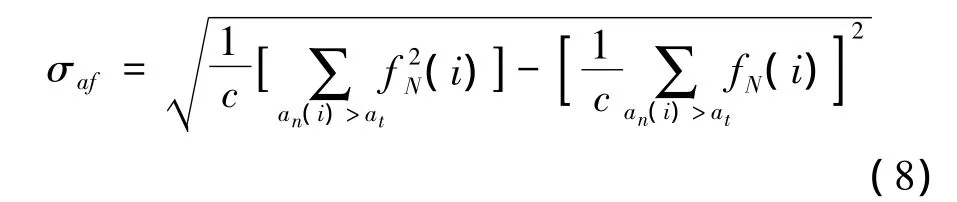
式中,
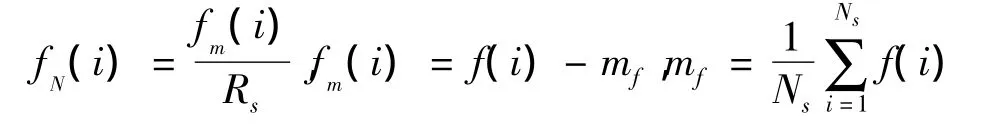
式中,Rs为数字信号的符号速率,f(i)为信号的瞬时频率。
2.2 粒子群优化算法
基于无线传感器网络的分布式协同信号识别的分类器设计部分采用粒子群算法对神经网络参数进行优化。在PSO中,粒子以一定的速度在搜索空间运动。在每一次迭代过程中,通过计算适应度函数,每个个体记下它经过的最优位置。个体根据自己先验知识和临域中其他个体的历史最优位置来改变自己的位置与速度,从而趋向全局最优。PSO的优势在于简单容易实现,并且没有许多参数需要调整。
设群体规模为N,在D维搜索空间中,第i(i=1,…,N)个粒子在搜索空间中的位置可以表示为x=(x1,x2,…xD),其飞行速度可以表示为 v=(v1,v2,…vD),则在第t+1代时,第i个粒子将根据下面的公式[8]来更新自己的位置和速度。

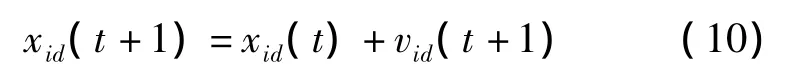
式中,d=1,…,D;pid为第i个粒子曾经到过的最佳位置,称为个体极值;pgd表示整个种群目前搜索到的最佳位置,称为全局极值;w是惯性权重;c1和c2为常数,称为学习因子或加速度系数;r1和r2是(0,1)上的随机数。每个粒子的个体极值由下面的公式来更新
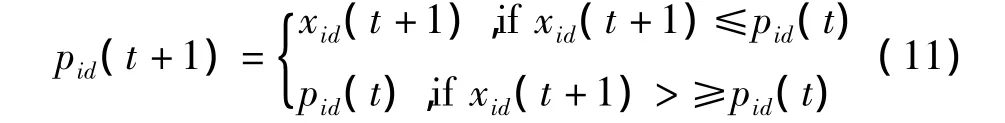
所有粒子的全局极值按如下方式选取。
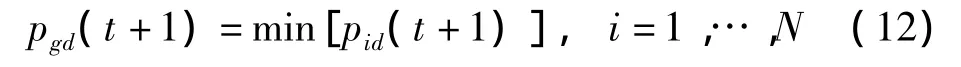
为使粒子飞行速度不致过大飞出搜索空间范围,可设置最大速度Vmax,当速度vi>Vmax时,取vi=Vmax;当 vi< - Vmax时,取 vi= - Vmax。
2.3 神经网络分类器的设计
为了避免反向传播网络(BP,back propagation)神经网络(又叫多层前馈网络)的收敛速度慢和局部极小值的局限性,采用径向基神经网络(RBF,radial basis functions),来提高其收敛速度和分类能力。假定输入样本为x,则隐含层第i个单元的输出为
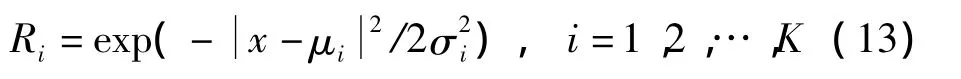
式中,K为隐含层单元的个数;μi为基函数的中心;σi为第i个隐含层单元的高斯函数的宽度,输出层节点的输出为
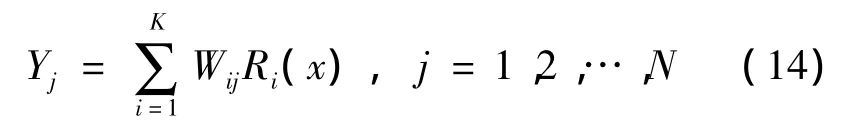
式中,Wij为第i个隐含层节点到第j个输出层节点的权值。N 为输出节点个数。μi,σi,Wij三个参数通过粒子群算法进行优化获得。神经网络的一组参数构成一个粒子的多维位置信息,把样本数据送入神经网络,记录目标输出与实际输出之间的误差和作为那个粒子的适应度值。算法步骤如下。
Step 1:对种群中粒子的位置和速度进行随机初始化;
Step 2:计算每个粒子的适应度;
Step 3:根据式(11)更新粒子的个体最优;
Step 4:根据式(12)更新全局最优位置;
Step 5:根据式(9)和(10)对粒子的速度和位置进行更新;
Step 6:如果没有达到终止条件(一般为预设最大迭代数或预设适应度值),则返回Step 2。否则转向Step 7。
Step 7:将测试数据送入训练好的神经网络,得到识别结果。
3 仿真结果
按照上述识别流程和算法对 2ASK,4ASK,2FSK,4FSK,BPSK,QPSK六种典型信号调制方式用MATLAB7.0进行了仿真。信噪比变化范围为0~5 dB,采样速率40 000,载波速率20 000,符号速率200,码元个数150。传感器数目选择50,各采样两次,分别作为神经网络的训练样本和测试样本。选用3层RBP神经网络,每组数据含五个特征参数,网络输入节点数为5,输出为六种调制方式的判断结果,输出节点数为6,设定隐含层节点数为5,每一种调制信号仿真100次。粒子群算法优化过程中,迭代次数250,粒子维数60,种群规模20,粒子数,粒子的范围:σi∈ [0.1,3],Wij∈ [ -1,1]。在信噪比为5 dB时系统输出最小误差进化过程,如图3所示。
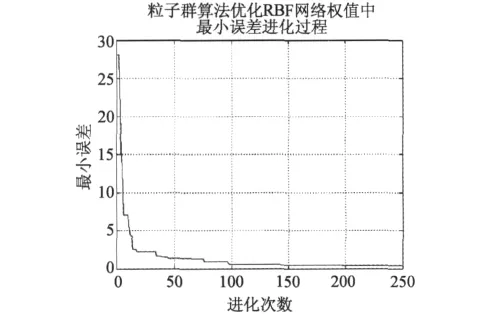
图3 粒子群算法优化RBF网络权值中最小误差进化过程
由图3可以看出,当粒子进化次数少于50次时,随着进化次数的增加,系统输出误差急剧降低;进化超过100次以后,系统输出误差变化较缓慢,接近于0。
传统的决策论方法调制识别率统计见表1。
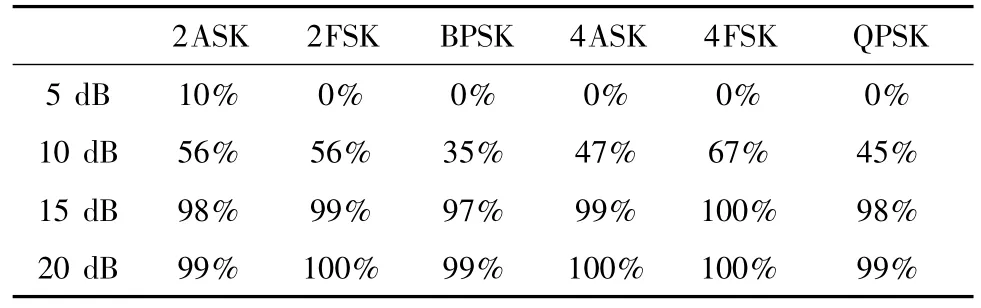
表1 基于传统决策论方法的调制识别率统计
集中式与分布式调制识别正确识别率见表2。

表2 集中式与分布式调制识别正确识别率对比
通过以上分析,可以得出如下结论。
(1)粒子群算法对神经网络参数优化过程中,迭代次数超过100次后能得到较低的输出误差;
(2)基于无线传感器网络的分布式调制识别在性能上优于基于传统决策论方法的调制识别方法;
(3)集中式信号调制识别的正确识别率与其所在的环境密不可分,在不确知周围环境条件时,采用基于无线传感器网络的分布式调制识别方法具有明显优势,5~25 dB时平均识别率达到90%以上;
(4)基于无线传感器网络的分布式调制识别方法存在的不足是识别时间较长,仿真情况下平均在一分钟以上。
4 结语
利用无线传感器网络提取特征参数,构成训练样本和测试样本,以目标输出与实际输出之间的误差和作为适应度函数,通过粒子群算法对径向基神经网络的参数进行优化,选择最优粒子所在位置作为神经网络的参数,利用训练好的神经网络进行识别分类。该方法与传统的基于决策论的识别方法相比,不需要预设判决门限,避免了判决门限值设置不合理的影响,且识别性能不受判决顺序的限制。仿真结果表明,该方法在低信噪比条件下识别性能明显优于基于决策论的方法和基于单节点进行识别的方法,平均识别率在5~25 dB时达到90%以上。
[1]XU J L,SU W,ZHOU M C.Likelihood Function-Based Modulation Classification in Bandwidth-Constrained Sensor Networks[C]//Networking,Sensing and Control(ICNSC),2010 International Conference on Chicago,IL:Institute of Electrical and Electronics Engineers,2010:530-533.
[2]XU J L,SU W,ZHOU M C.Distribute Automatic Modulation Classification with Multiple Sensors[J].IEEE Sensors Journal,2010,10(11):1 779-1 785.
[3]FORERO P,CANO A,GIANNAKIS G.Distribute Feature-Based Modulation Classification Using Wireless Sensor Networks[C]//Military Communications Conference,2008.San Diego,CA:Institute of Electrical and Electronics Engineers,2008:1-7.
[4]刘爱声,朱琦.多传感器节点分布式协作调制识别算法[J].信号处理,2011,27(8):1 235-1 241.
[5]党月芳,徐启建,张杰.无线传感器网络分布式频谱检测研究[J].中国电子科学研究院学报,2012,7(1):21-28.
[6]ZHAO YA-QIN,REN GUANG-HUI,WANG XUE-XIA.Automatic Modulation Recognition Using Artificial Neural Network[C]//Proceedings of the 2003 International Conference on Neural Networks and Signal Processing.2003 International Conference on.Neural Networks and Signal Processing.United States:Institute of Electrical and Electronics Engineers,2003:257-260.
[7]WANG BIN,GE LIN-DONG.A Novel Algorithm for Identification of OFDM Signal[J].IEEE Transactionson Communication,2005,53(1):261-264.
[8]LIU J,HU Y Q.A New Algorithm for Digital Modulation Recognition Under the Low SNR[J].Systems Engineering and Electronic,2009,31(6):60-64.
[9]王宇嘉.多目标粒子群优化算法的全局搜索策略研究[D].上海:上海交通大学,2008.

