求取电压稳定分歧点的改进步长连续潮流法

贺泳华， 刘光晔， 高 磊

(1.湖南大学电气与信息工程学院， 长沙 410082；2.西北电网西安输变电运行公司， 西安 710065)

求取电压稳定分歧点的改进步长连续潮流法

贺泳华1， 刘光晔1， 高 磊2

(1.湖南大学电气与信息工程学院， 长沙 410082；2.西北电网西安输变电运行公司， 西安 710065)

连续潮流法是求取电压稳定分歧点的一种有效方法，但现有方法计算量大。为此，提出一种改进步长连续潮流法，先对线性电路的戴维南等值原理进行广义扩充，证明了非线性电力系统传输最大功率条件是：戴维南动态等值阻抗模等于负荷静态等值阻抗模。并根据戴维南动态等值阻抗引导的负荷阻抗变化初步预测极限功率，以此作为连续潮流计算的步长选择依据，实现变步长连续潮流计算。对IEEE118系统进行仿真计算，结果表明该算法能既快速又准确地找到电压稳定分歧点。

电压稳定极限点； 广义戴维南等值原理； 连续潮流； 步长控制； 静态电压稳定

近年来，随着电力系统规模的不断扩大以及电网互连的确立，电压不稳定事故也常常发生[1]，由于电力系统的电压失稳大多是单调失稳，因此静态电压稳定问题逐渐成为国内外学者非常关注的课题。静态电压稳定研究中，稳定分歧点的求取十分重要。稳定分歧点也称极限点，目前极限点的求取方法主要有：非线性规划法[7]，零特征法[2]和连续潮流法[5]等。

连续潮流CPF(continuation power flow)法是系统静态稳定分析的重要方法，CPF通过在常规潮流方程基础上增加连续性参数，改动潮流方程，从而克服了雅科比矩阵在接近分歧点的奇异问题，能够比较准确地求取电压稳定极限点[3，4，6]。

传统的连续潮流法因为需要从当前运行点逐渐增加步长，逐步计算到电压分歧点，所以在连续潮流法中，步长的选择很重要。步长选择过长，能提高计算效率，但可能导致越过极限点或不收敛；步长选择过短能精确找到极限点，但计算效率低[6]。最理想的方法是在基态点附近选择大步长，以求快速接近分歧点，在临近分歧点时选择小步长，以求精确求出分歧点[7]。针对这一问题，许多学者提出了不同的解决方案[3，7，9]：文献[7]中提到一种指标预估的改进步长法，文献[9]中提到利用幂函数特性来确定步长的方法。虽然这些步长控制方法或多或少减少计算量[9]，但由于不知道极限点的大致位置，不能有效地提高计算效率。

本文提出一种基于广义戴维南等值原理的改进步长连续潮流法，根据广义戴维南等值原理得出的电压稳定阻抗模指标来预测极限潮流点，将预测到的负荷因子用到步长控制环节，实现自动调节步长，从而快速准确地得到电压稳定极限点。

1 连续潮流原理

连续潮流是指随着负荷的增长，沿PV曲线对一下个潮流解进行预测，校正，逐步地求解潮流，直到求得电压稳定分歧点的一种方法[10]。大致可以分为以下部分[8]：参数化，预测，步长控制，校正。具体步骤如下。

1)参数化

参数化是选择连续性参数，构造一个方程，使得它与参数化的潮流方程一起构成一个具有n+1维方程组。从而改变了系统雅科比矩阵的结构，来避免奇异问题[8]。常用的方法有局部参数法[4]，弧长参数法[3]等。

2)预测步

预测步是沿着负荷变化因子增长方向预测下一个解。预测步有切线预测[4]和多项式外插等方法[7]。切线法的公式为

(1)

式中，ek为除了与连续性参数的位置相对应的第k个元素为1外，其余为0。

3)步长控制

步长控制的选取是决定连续潮流方法有效性的一个关键所在，选取得当能减小计算量。根据式(1)所确定的预测方向，再由步长公式算出σ后，可计算预测点(其中σ为步长)，其公式为

(2)

4)校正步

(3)

2 广义戴维南的改进步长法原理

在静态电压稳定分析方法中，面向负荷节点的戴维南等值方法，可以有效地简化系统网络，快速分析节点电压稳定性。由于该方法简单直观，所以在近年来得到了广泛的研究[10～13]：文献[10]通过建立比函数来跟踪估计节点的戴维南等值参数，文献[11]对等值跟踪过程中的参数漂移的本质进行了分析。这些文献虽然取得了一定的成果，但其在状态点的选取上至少需要两个潮流点，并假设两个状态点之间的戴维南等值参数不变，当两个状态点间隔较大，则其戴维南等值参数就会发生变化；当间隔较小，则可能遇到病态方程组带来的数值不稳定现象，就会导致出现参数漂移问题。为了解决这个选取困难问题，本文提出一种广义戴维南等值原理，可以只选用一个状态点就可以求出戴维南等值参数，并快速预测潮流。

2.1 广义戴维南等值原理(简化网络)

在线性电路中，复杂网络可简化成戴维南等值网络。如图1所示，根据最大传输功率定理：节点负荷阻抗模等于戴维南阻抗模时传输功率最大[10]。

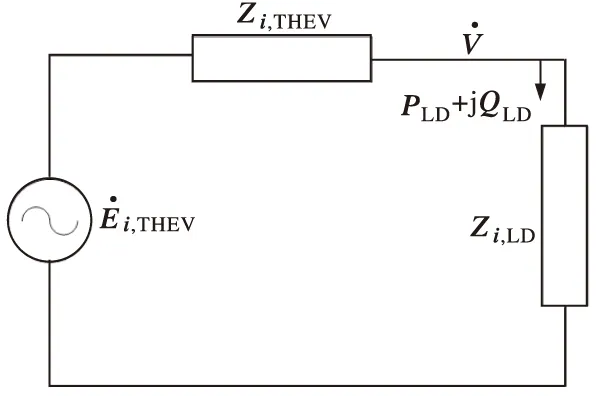
图1 简单系统等值电路

同样在非线性电路中，经过证明也可得到这一结论，本文将其称为广义戴维南等值原理，证明如下：

广义戴维南动态等值阻抗用Zi,THEV表示，负荷静态阻抗模用Zi,LD表示即

Zi,LD=Vi/Ii

(4)

定义广义戴维南等值阻抗为非线性电源内阻抗

(5)

设电压与电流的函数关系式为

(6)

将式(6)带入式(5)并将式(6)中的电流正交分解可得

(RTHEV+jXTHEV)(dIx+jdIy)

(7)

通过求偏导可得RTHEV和XTHEV。

对于上面分析的恒电势的线性电路的戴维南等值电路，有

(8)

正交分解可得到

(9)

则负荷吸收的复功率的表达式为

PLD+jQLD=fxIx+fyIy+j[fyIx-fxIy]

(10)

设负荷功率恒定

kPLD-QLD=0

(11)

其中k为常数。构造拉格朗日函数

FP(Ix，Iy)=PLD+λ(kPLD-QLD)

(12)

式中，λ为拉格朗日常数，将式(10)代入式(12)中根据拉格朗日常数法，式(10)中的有功功率取得极值的必要条件为

(13)

将式(5)和式(6)代入式(13)得

(14)

即

|ZLD|=|ZTHEV|

(15)

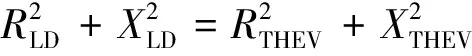
kPLD+C-QLD=0

(16)

式中，C为常数。

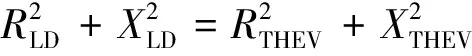
通过上述证明可以得到，在动态非线性电路中的每一个负荷节点获得最大功率的必要条件是负荷静态阻抗模与广义戴维南动态等值阻抗模相等，此时负荷节点电压临界稳定，这一点与在线性电路中的结论是类似的。根据证明的非线性电力系统负荷节点获得极大值必要条件，只要在选定的一个初始点，进行一定计算，就可以预测到下一个状态。

2.2 广义戴维南等值原理预测潮流

对于任一PQ节点，广义戴维南等值阻抗计算过程为

(17)

(18)

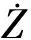
(19)

节点i的预测潮流为

(20)

其中

由于假设的系统有功功率与无功功率同步增长，所以复功率对应的预测功率倍数与有功功率对应的预测功率倍数相等，即

λ1=Pi,yc/Pi0=Si,yc/Si0

(21)

式中，λ1为预测到的下一个负荷变化因子。

2.3 广义戴维南等值原理的步长控制算法

在潮流初始点(λ=0)，用牛顿法求得初始潮流解A1。确定系统的薄弱节点后，使用局部参数化，用切线法进行预测得到预测方向(dx，dλ)。用式(17)～式(22)即根据广义戴维南等值原理得出的电压稳定阻抗模指标来预测在当前潮流点的下一个潮流状态，得到负荷增长因子λ1。代入式(2)中，得到步长σ，其公式为

σ=(λ1-λ0)/dλ

(22)

式中，λ0为当前潮流点的负荷增长因子。

算法的流程如图2所示。

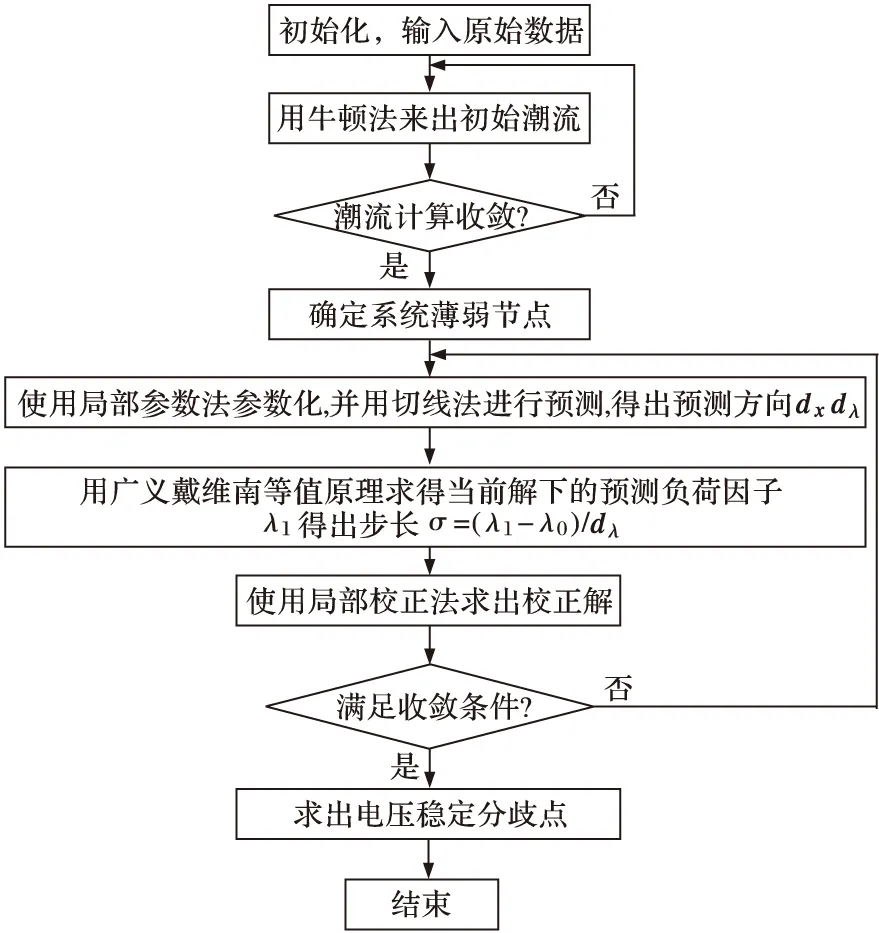
图2 算法流程

3 仿真计算与分析

对IEEE118节点系统进行仿真，其负荷增长方式如下：系统负荷功率同步增加，电源功率按初始功率比例分摊，网损变化由平衡节点承担。并考虑PV节点无功功率约束。

用基于广义戴维南等值原理得出的电压稳定阻抗模指标来预测IEEE118节点系统的薄弱节点(41号节点)在当前潮流点的下一个潮流状态、当前状态下的广义戴维南动态等值阻抗模|Zi,THEV|和负荷静态阻抗模|Zi,LD|及得到的新的负荷增长因子λ1，如表1所示。

从表1中可看出：随着负荷因子的增大，基态点附近(1.0～2.0)预测到的较远处的负荷因子，临近极限点(2.0以后)预测到较近处的负荷因子，证明其可直接用于步长控制环节。

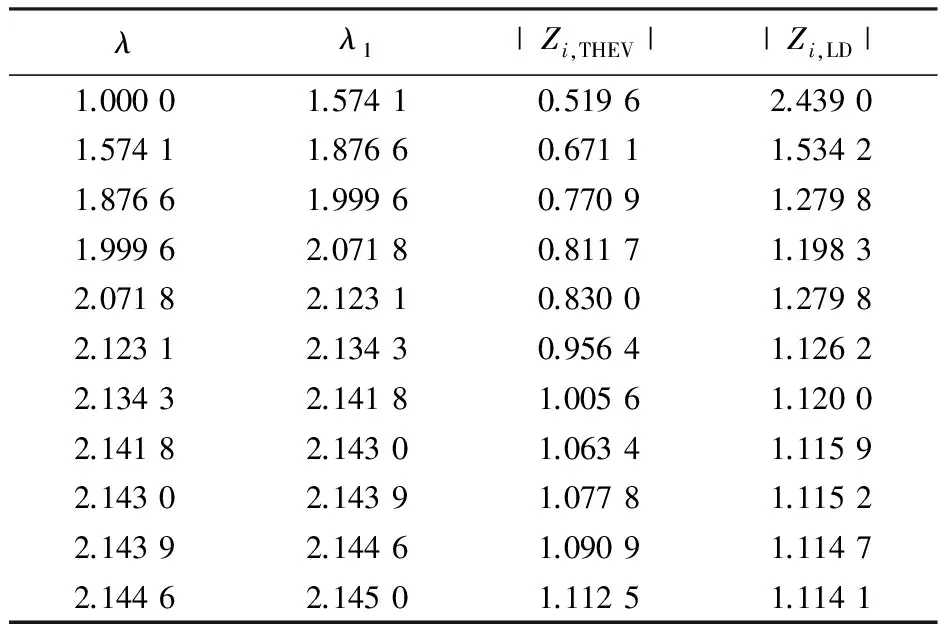
表1 λ的预测

逐步增加负荷变化因子λ，用所提改进步长连续潮流算法求得的薄弱节点(41号节点)的电压稳定极限点的负荷因子λcr，极限电压Vcr并与未采用自动变步长法的定步长连续潮流法的算法(步长取0.01)进行比较，如表2所示。

表2 两种算法比较

分析表2与表1得知：

(1)表1中λ=2.145 0时|ZTHEV|与|ZLD|大致相等，按照广义戴维南等值原理此时应该接近电压稳定临界点。表2中，电压稳定分歧点为λ=2.145 02，由此证明了广义戴维南等值原理的准确性。

(2)采用自动变步长的连续潮流法不仅可以准确求出电压稳定分歧点，与常规连续潮流相比运行点数目大大减小，提高了计算效率。

4 结论

(1)证明了在非线性系统每一个负荷节点，其负荷功率获得极大值必要条件是：戴维南动态等值阻抗模等于负荷静态阻抗模，通过一个状态点就能快速预测到潮流，解决了戴维南等值原理的参数漂移问题。

(2)应用非线性系统极大传输功率预测负荷变化因子，提出了基于广义戴维南等值原理的改进步长连续法，可以实现自动变步长，缩短连续潮流计算时间，并准确计算电压稳定极限点。

[1] 胡学浩(Hu Xuehao). 美加联合电网大面积停电事故的反思和启示(Rethinking and enlightenment of large scope blackout in interconnected north America power grid)[J].电网技术(Power System Technology)，2003，27(9):T2-T6.

[2] 曾江，韩祯祥(Zeng Jiang，Han Zhenxiang). 电压稳定临界点的直接计算法(Direct method for calculating critical point of voltage stability)[J]. 清华大学学报：自然科学版(Journal of Tsinghua University：Science and Technology)，1997，37(S1): 91-94.

[3] Chiang Hsiao-dong, Flueck A J, Shah K S,etal.CPFLOW: A practical tool for tracing power system steady-state stationary behavior due to load and generation variations[J].IEEE Trans on Power Systems，1995，10(2):623-634.

[4] Ajjarapu V, Christy C. The continuation power flo-w: a tool for steady state voltage stability analysis[J].IEEE Trans on Power Systems,1992,7(1):416-423.

[5] 祝达康，程浩忠(Zhu Dakang，Cheng Haozhong).求取电力系统PV曲线的改进连续潮流法(An improved continuation method in tracing PV curves of power systems)[J].电网技术(Power System Technology)，1999，23(4):37-48.

[6] 张尧，张建设，袁世强(Zhang Yao, Zhang Jianshe,Yuan Shiqiang).求取静态电压稳定极限的改进连续潮流法(Improved continuation power flow algorithm for obtaining the limit of static voltage stability)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA) ，2005，17(2):21-25.

[7] 赵晋泉，张伯明(Zhao Jinquan，Zhang Boming).连续潮流及其在电力系统静态稳定分析中的应用(Summarization of continuation power flow and its applications in static stability analysis of power system)[J].电力系统自动化(Automation of Electric Power Systems)，2005，29(11)：91-97.

[8] 张伯明，陈寿孙，严正.高等电力网络分析 [M].北京：清华大学出版社，2007.

[9] 王成山，魏炜(Wang Chengshan，Wei wei). 一种改进的步长控制连续性潮流计算方法(An improved continuation method with controlled step size)[J].电工技术学报(Transactions of China Electrotechnical Society)，2004，19(2)：58-63.

[10]王漪，柳焯(Wang Yi,Liu Zhuo).基于戴维南等值的系统参数跟踪估计(Tracking and estimation of system parameter using Thevenin's equivalent)[J].电网技术(Power System Technology)，2000，24(11):28-30.

[11]李来福，于继来，柳焯(Li Laifu，Yu Jilai，Liu Zhuo). 戴维南等值跟踪的参数漂移问题研究(Research on parameters drift problem in tracking Thevenin equivalent)[J].中国电机工程学报(Proceedings of the CSEE)，2005，25(20)：1-5.

贺泳华(1986-)，女，硕士研究生，研究方向为电压稳定研究。Email:hyh123abc@163.com

刘光晔(1960-)，男，博士，教授，博士生导师，研究方向为电力系统分析与控制、电力系统继电保护研究。Email:liuguangye@21cn.com

高 磊(1986-)，男，本科生，助理工程师，主要从事电力系统二次设备调试与研究。Email:sxwm_2009@163.com

ImprovedContinuationMethodwithControlledStepSizefortheSolutionofVoltageStabilityBifurcation

HE Yong-hua1， LIU Guang-ye1， GAO Lei2

(1.College of Electrical and Infomation Engineering, Hunan University,Changsha 410082, China；2.Northwest Xi'an Power Transmission Operation Company, Xi'an 710065, China)

Continuation power flow algorithms are effective for obtaining the voltage stability bifurcation, but the calculation scale of existing methods is large. An improved continuation power flow method with controlled step size which predicts limit power flow is presented. First it extends Thevenin equivalent theory in linear circuit．It is proved that the maximum power transmission in power system is in a necessary condition：Thevenin dynamic equivalent impedance modul should be equal to the load equivalent impedance modul. This algorithm uses predicted limit power flow based on the load impedance change lead by Thevein dynamic equivalent impedance to adjusts step size automatically，which can be proved accurately and effectively to obtain the voltage stability bifurcation in IEEE 118 standard system.

voltage stability limit of power system； extended Thevenin equivalent theory； continuation power flow； step size controlling； static voltage-stability

TM71

A

1003-8930(2012)05-0112-05

2011-03-21；

2011-04-22