直驱永磁型风电系统的小扰动稳定性分析

李军军， 吴政球， 谭勋琼

(1.湖南大学电气与信息工程学院， 长沙 410082；2.湖南工业大学电气与信息工程学院， 株洲 412008)

直驱永磁型风电系统的小扰动稳定性分析

李军军1，2， 吴政球1， 谭勋琼1

(1.湖南大学电气与信息工程学院， 长沙 410082；2.湖南工业大学电气与信息工程学院， 株洲 412008)

建立了基于双PWM变换器的直驱永磁型风电系统的小扰动稳定性分析数学模型，研究了风电系统并网后参数变化对电力系统稳定性的影响，得到了一些有意义的结论；为保证风电系统最大功率输出，风力机采用了最大功率点跟踪控制策略；研究了机侧和网侧变换器控制结构；利用Matlab建模仿真，对系统在不同参数条件下进行了时域分析。仿真结果表明，不同的参数条件下，系统具有较好的小扰动稳定性，验证了理论分析的正确性，为直驱永磁型风电系统安全稳定地并网运行提供了可借鉴的理论依据。

永磁同步机； PWM变换器； 小扰动稳定； 最大功率点跟踪

变速恒频发电是目前国内外风电技术的主流，机组通常采用双馈型发电机，系统通过齿轮箱连接风力机和发电机，双馈电机带有电刷和滑环，系统结构较复杂，降低了运行的可靠性[1]。直驱永磁型风电系统省去了电刷、滑环和齿轮箱，减少了系统的维护及成本，可靠性高。双脉冲宽度调制PWM(pulse width modulation)变换器的直驱永磁型风电系统不但能实现变速恒频运行，并网有功和无功还能够独立控制，具有发电效率高，结构简单，运行稳定等特点，得到了广泛的应用。随着风电规模的不断扩大，风电并网运行的稳定性问题日益突出，已成为研究的重要课题之一，建立风力发电系统数学模型进行小扰动稳定性分析，并进行仿真是重要的研究手段之一。文献[2]对双PWM变换器的直驱永磁型风电系统的动态、静态特性进行了建模仿真研究；文献[4]研究了在最佳风能追踪控制下，直驱永磁型风电系统机侧和网侧变换器的控制策略；文献[5～8]研究了电压型PWM变换器的数学模型及其控制策略；文献[9]研究了电流型双PWM变换器的直驱永磁型风电系统的小信号模型，分析了系统参数变化对系统稳定性的影响。

本文在对上述文献研究的基础上，建立了双PWM变换器的直驱永磁型风电系统的小信号稳定性分析数学模型；研究了最大功率点跟踪控制策略，使风电系统输出功率最大；设计了双PWM变换器的控制方案，并在此基础上分析了参数变化对系统小扰动稳定性的影响；通过建模对系统在不同参数条件下进行了时域仿真，对理论分析进行验证。

1 双PWM变换器的直驱永磁型风电系统模型

系统结构如图1所示。由风轮机、永磁同步电机、双PWM变换器、网侧阻抗及电网组成。

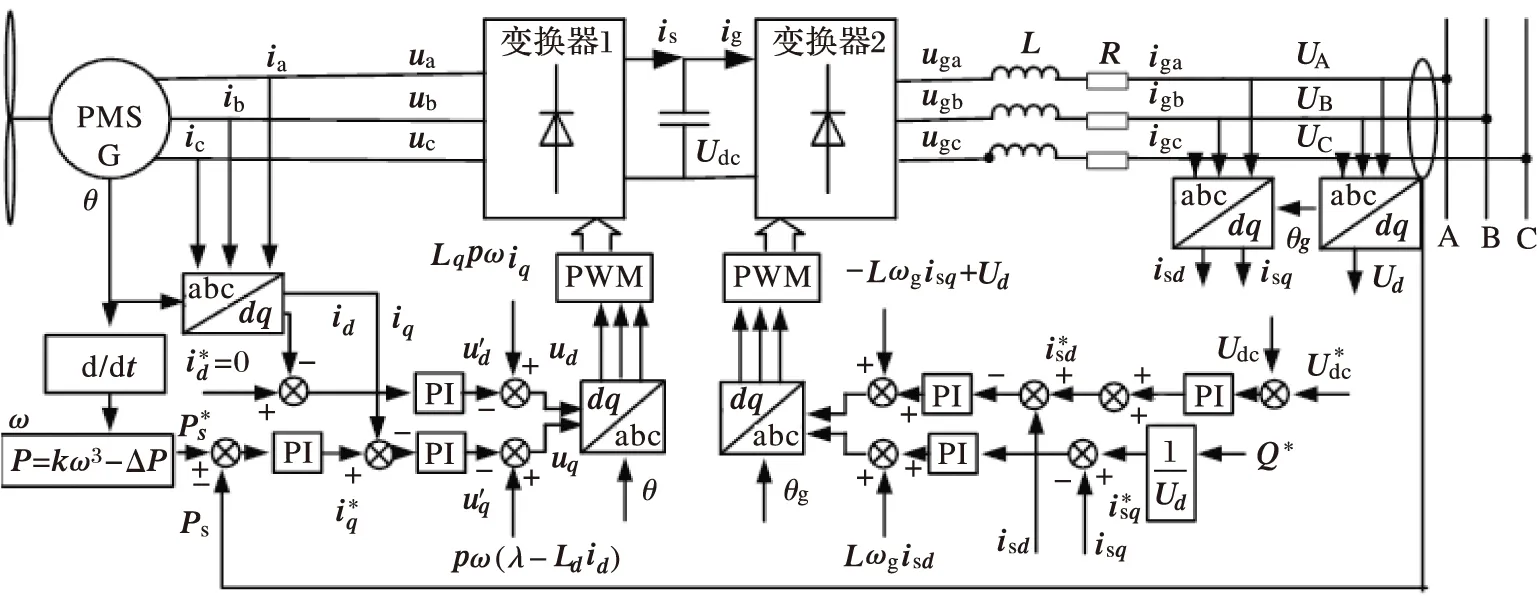
图1 直驱型永磁风电系统

1.1 风轮机

风轮机产生的机械功率为

(1)

其中：ρ为空气密度；r为叶片半径；vm为风速；λ为叶尖速率比；Cp为风轮机转换效率，是λ和桨距角β的非线性函数。

1.2永磁同步电机PMSG模型

dq坐标系下，PMSG的电气部分方程

(2)

机械部分方程

dω/dt=1/J(Tm-Te-Fω)

(3)

PMSG电磁转矩

Te=1.5p[γiq+(Ld-Lq)idiq]

(4)

式中：Rs为定子电阻；γ为磁链；ω为转子机械角转速；Ld、Lq为定子dq轴电感；ud、uq(id、iq)为定子dq轴电压(电流)；F为转子阻尼系数；J为转子转动惯量；Tm为风轮机输出机械转矩；p为极对数。

1.3 网侧模型

如图1所示，电网电压综合矢量定位d轴，网侧dq坐标系下方程

(5)

式中：ugd、ugq、isd、isq为变换器2输出的电压和电流；Ud为电网电压；ωg为电网角频率；R、L网侧电阻和电感。

1.4 双PWM变换器数学模型

变换器2输出电压与直流电压关系为

(6)

Sk开关函数，三相桥臂上管导通、下管关断时为1；上管关断，下管导通时为0。dq变换后，得

(7)

式中，Sd2、Sq2为dq坐标系下的开关函数。直流电流ig与网侧交流电流关系

ig=Sa2isa+Sb2isb+Sc2isc

(8)

dq变换后，得

ig=1.5(Sd2isd+Sq2isq)

(9)

同理，变换器1输入端电压、电流与直流电压、电流也满足类似的关系。

直流电容器的电压，电流满足

CdUdc/dt=is-ig

(10)

式中：is、ig为变换器1、2的输出、输入电流。

1.5 小信号交流模型

结合式(2)、式(3)、式(5)和式(8)～式(10)构成了系统的状态方程，经整理后(考虑隐式PMSG，Ld=Lq)，得

(11)

式中：isd、isq、Udc、id、iq、ω为状态变量；Ud、Uq为输入量；而中间变量ugd、ugq、ud、uq需从方程中消去。由于开关函数Sd1、Sq1和Sd2、Sq2是时间的非连续函数，不利于控制系统分析和设计。对开关函数Sk进行傅里叶分解[5]可得

(12)

Sk既含有直流分量，又含高频分量，忽略开关函数中相关的高次谐波，sa、sb、sc可用占空比da、db、dc代替。

根据文献[11]的描述方法，可得系统的小信号交流模型为

(13)

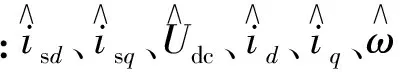
模型(13)在小扰动稳定性分析时很方便。其矩阵形式表示为

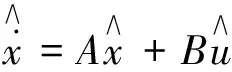
(14)

若A所有特征值均有负实部，系统在小扰动下系统是稳定的。

2 最佳功率追踪控制

当桨距角一定时，风力机叶尖速比保持最佳，就可获得最大风能利用系数Cpmax，实现最大风能捕获。因此，最大风能跟踪的要求是在风速变化时适时调整风力机转速，使其始终维持最佳叶尖速比λopt[12]。最佳功率Pm-opt只与风轮转速有关，即

Pm-opt=kω3

(15)

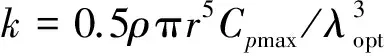
在网侧，若忽略变换器自身及线路损耗，根据功率不变原则有

Pg=ugaisa+ugbisb+ugcisc≈

Uaisa+Ubisb+Ucisc

(16)

网侧有功、无功可表示为

(17)

经坐标变换实现了有功和无功的解耦。

忽略变换器自身损耗，仅考虑PMSG定子铜耗，有

(18)

机侧功率存在以下关系

Pm=Pe+ΔP

(19)

式中，Pe为PMSG电磁功率

当机侧、网侧功率满足以下关系时系统达到稳态，即

PM-ΔP=Pg

(20)

3 双PWM变换器的控制策略

网侧和机侧变换器的控制结构如图1所示。机侧变换器采用双环控制结构：功率外环和电流内环。外环的主要作用提供电流内环参考值；电流内环按功率外环的输出指令进行电流控制。从式(4)可知PMSG定子dq轴电流id、iq间存在耦合，可引入前馈信号，实现解耦。同时id=0，电磁转矩由q轴电流决定，相当于直流电机的控制，最简单也最实用。

网侧变换器也采用双环控制结构，即直流电压外环与电流内环。外环的主要作用是保持直流电压的稳定，并给电流内环提供参考信号。从式(5)可知，网侧电流dq轴分量isd、isq也存在耦合，同样可以像机侧那样引入前馈信号。isd相当于有功电流，isq相当于无功电流，若要网侧变换器工作于单位功率因数状态，可使isq=0。

4 特征值分析

求解A的特征值，分析参数变化对系统稳定性的影响。当机侧和网侧功率满足式(20)时，则可认为系统处于稳态，计算得直流工作点值(均为实名制，系统有关参数见附录)：ud=195.1 V，uq=552.3 V，Iq=1 191.6 A，Id=0，Ud=311.12 V，Uq=0，Isq=0，Isd=2 115.4 A，Udc=1 200 V，Dd1=0.162 6，Dq1=0.460 3，Dd2=0.259 3，Dq2=0.166 1，ω=2.28 rad/s，风速vm=11 m/s。

PWM调制中，设调制波为mi=Mcos(ωt+δ)，δ在机侧为PMSG感应电动势ei与电枢电压(即机侧变换器输入电压)ui的夹角(i=a，b，c)，在网侧δ为ugi与Ui的夹角。调制深度M，当0≤M≤1时调制效果最好，占空比与调制波有R关系为

di=(mi+1)/2

(21)

另外三相电压型变换器输入端电压与调制电压、直流电压间的关系为

(22)

在机侧，经dq变化可得

(23)

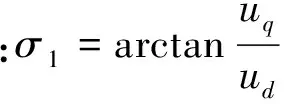
代入有关参数，计算得σ1=70.545 1°，M1=0.976 2。同理，可得σ2=32.639 5°，M2=0.615 8，由此确定了机侧和网侧的调制信号。

4.1 改变线路电感值

表1数据表明，改变线路电感对机侧无影响，对网侧影响较大，虽然增大电感可改善滤波效果，但网侧变换器调制深度M2gt;1，调制效果变差。连接风力机与电网的线路阻抗大小表示风力机与系统联系的紧密程度，阻抗小，可提高功率输送能力，有利于系统的稳定性。表2数据表明，增大线路电感，特征值右移，稳定性变差，与实际情况相吻合。

表1 改变线路电感时参数的变化

表2 改变线路电感时特征值的变化

4.2 改变母线电压值

表3和表4显示，母线电压增大，参数变化较小，系统的小扰动稳定性有所提高，在实际情况中，适当提高电压，有利于提高系统的功率输送能力，对系统的稳定性是有利的。

4.3 改变直流电容值

表5数据表明，增加电容值对机侧、网侧无影响；表6显示，特征值实部绝对值有所增大，系统的稳定性增强，因此合适的直流电容对系统的稳定性是有利的。在风电系统中，为避免直流电压波动，常引入大电容，而大电容的引入必然会带来成本的提高，重量、体积的增大，这在兆瓦级风电系统中尤为明显；同时大电容的引入加大了电压环的时间常数，减慢了电压环的响应速度，从上述原因考虑，直流电容的值不宜过大。

表3 母线电压改变时参数的变化

表4 母线电压改变时特征值的变化

表5 改变直流电容时参数的变化

表6 改变直流电容时特征值的变化

4.4 改变风速

表7和表8表明，额定风速以上改变风速，对系统的稳定性不利。由于采用最佳风能追踪控制，当风速增大，PMSG转速、输出功率均增大，网侧电压、电流也有较大增加；同时风速增大，机侧和网侧变换器调制深度大于1，影响调制效果，为保证系统安全运行应增加浆距角控制将多余的风能除去，但由此降低了发电效率。

表7 改变风速时相关量的变化

表8 改变风速时特征值的变化

5 仿真

本节通过建模仿真对理论分析结果加以验证。要求：机侧id=0，电磁转矩及电磁功率取决于iq；直流电压调制到1 200 V，且保持恒定；网侧isq=0，有功等于机侧输出有功，无功为零，改变参数时系统能否保持小扰动稳定。仿真参数按附录设置，仿真时间5 s，仿真波形如图2～图11所示。图2所示，PMSG转速与稳态时计算的基本一致；机侧电流id=0，如图3所示；机侧变换器的调制深度与调制角度与计算的值比较接近，如图4～图5所示，而网侧变换器的有一定差异，如图8～图9所示；网侧变换器向电网输送有功达1 MW，无功为0，如图10所示；直流电压达到1 200 V，恒定不变，如图11所示；网侧电流谐波THD=4.33%lt;5%，满足要求。

篇幅所限，仅给出改变线路电感和改变风速时的仿真结果。线路电感从0.3 mH增大至0.8 mH，其余参数保持不变。仿真波形如图12～图15所示，从仿真结果来看，直流电压、网侧变换器输出有功、电流均有小幅波动，且电感值越大波动越大。因此，电感值过大不利于系统的小扰动稳定性，与理论分析是一致的。

图2 PMSG转速

图3 PMSG dq 轴电流

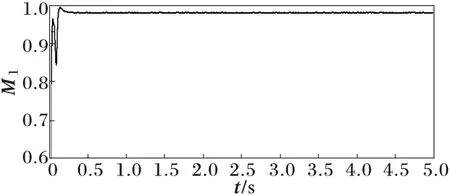
图4 PMSG侧变换器调制深度M1

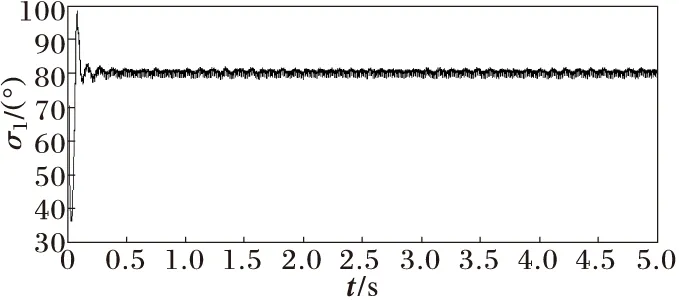
图5 PMSG侧变换器调制角σ1

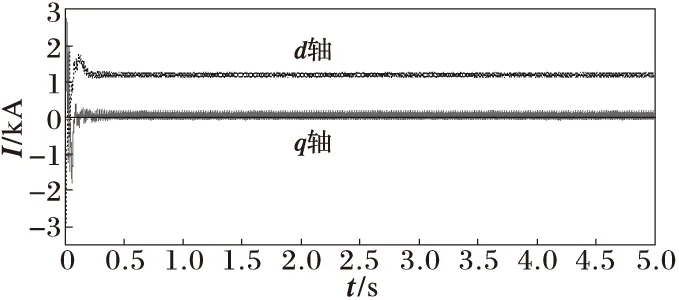
图6 网侧dq轴电流

图7 网侧dq轴电压

图8 网侧变换器调制深度M2

考虑改变风速(见图16)时(其他参数不变)对系统稳定性的影响。仿真波形如图17～图21所示，从仿真结果来看，风速增加使得输出功率、直流电压、网侧电流有所增加，并且机侧调制深度M1gt;1，与理论分析一致，若不通过浆距角调节，过大的风速对系统的小扰动稳定是不利的。

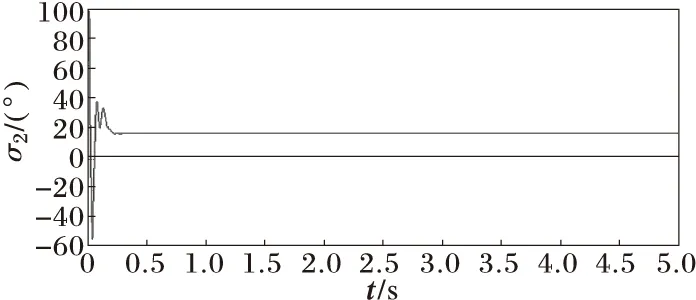
图9 网侧变换器调制角σ2

图10 网侧变换器向电网输送的功率

图11 直流电压

图12 改变线路电感时PMSG dq 轴电流

图13 改变线路电感时网侧dq轴电流

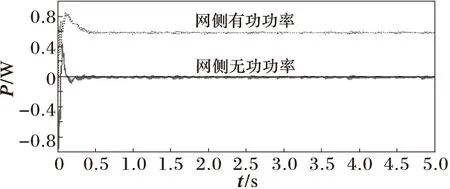
图14 改变线路电感时网侧变换器向电网输送的功率

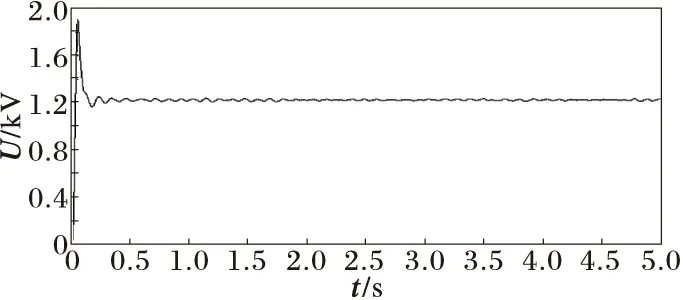
图15 改变线路电感时直流电压

图16 风速变化情况

图17 改变风速时PMSG dq 轴电流

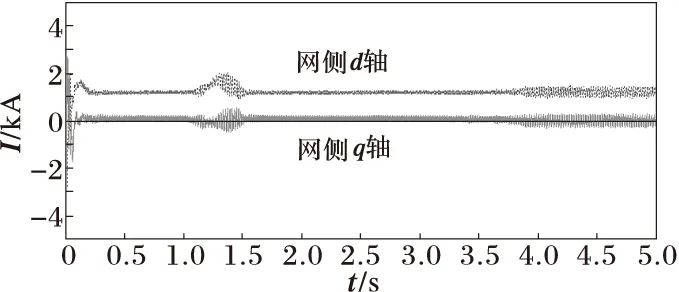
图18 改变风速时网侧dq轴电流

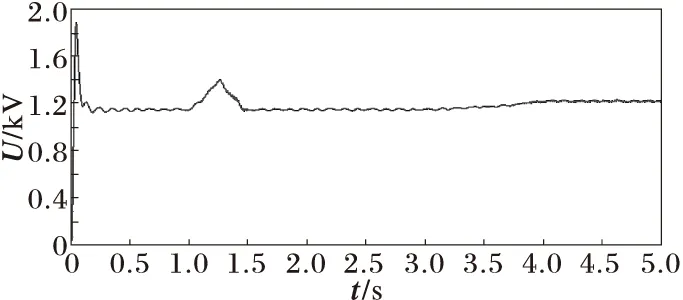
图19 改变风速时直流电压

图20 网侧变换器向电网输送的功率

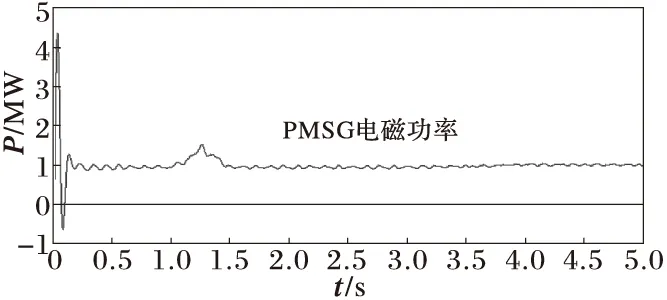
图21 PMSG输出电磁功率

6 结语

通过研究发现，不同的参数运行条件对系统的小扰动稳定性有一定的影响，仿真试验也验证了理论分析的正确性。若要保证系统具有较好的小扰动稳定性，线路电感不宜过大；直流电容要取值合适；母线电压可适当提高；增加浆距角调节机构，以保证系统在额定风速以上能安全地运行，为直驱永磁型风电并网安全稳定运行提供了可借鉴的理论依据。

附录A

PMSG：

额定容量1 MW；定子额定电压690 V，定子额定电流850 A，p=28，Rs=0.006 Ω，额定转速2.3 rad/s，Ld=Lq=2.56 mH，λ=8.748，J=5 000 kg·m2，F=0；Udc=1 200 V，C=38 mF。

线路：

L=300 μH；R=3.5 mΩ。

电网频率50 Hz。

电网电压380 V。

风轮机：ρ=1.225 kg/m3，β=0°，r=30 m，λopt=6.25，Cpmax=0.438 2。

PI调节器：kp1=0.5，Ti=0.05，kp2=0.1；开关频率为6 kHz，kpwm=1 200。

[1] 胡书举，李建林，许洪华(Hu Shuju， Li Jianlin， Xu Honghua).永磁直驱风电系统变流器拓扑分析(Analysis of converter configuration for direct-drive wind power system with PMSG)[J].电力自动化设备(Electric Power Automation Equipment)， 2008， 28(4)：77-81.

[2] 胡书举，赵栋利，李建林,等(Hu Shuju，Zhao Dongli， Li Jianlin,etal).基于永磁同步发电机的直驱风电双脉宽调制变流器的研制(Development on dual-PWM converter for direct-driven wind power system based on PMSG)[J].动力工程(Journal of Power Engineering)，2009，29(2)：195-200.

[3] 谢震，张兴，曹仁贤(Xie Zhen，Zhang Xing， Cao Renxian). 双馈风力发电用交直交变流器控制策略的研究(Study on the control strategy of AC-DC-AC converter used in wind turbine system driven by doubly fed induction generator)[J].太阳能学报(Acta Energlae Solaris Sinica)，2007，28(8)：825-829.

[4] 姚骏，廖勇，瞿兴鸿(Yao Jun， Liao Yong， Qu Xinghong).直驱永磁同步风力发电机的最佳风能跟踪控制(Optimal wind energy tracking control of direct-driven permanent magnet synchronous generators for wind turbines)[J].电网技术(Power System Technology)，2008，32(10)：11-15,27.

[5] 李建林，王立乔，熊宇,等(Li Jianlin，Wang Liqiao， Xiong Yu,etal).三相电压型变流器系统静态数学模型(A static-state mathematical model of three-phase voltage source converter)[J].电工技术学报(Transactions of China Electrotechnical Society)，2004，19(7)：11-15.

[6] 裘迅，方宇，王儒,等(Qiu Xun，Fang Yu，Wang Ru,etal). 三相高功率因素电压型PWM整流器控制策略(Control strategy of three phase high power factor PWM rectifier)[J]. 电工技术学报(Transactions of China Electrotechnical Society)，2008，23(11)：96-102.

[7] 王久和，李华德，王立明(Wang Jiuhe, Li Huade, Wang Liming).电压型PWM整流器直接功率控制系统(Direct power control system of three phase boost type PWM rectifiers)[J].中国电机工程学报(Proceedings of the CSEE)，2006，26(18)：54-60.

[8] 瞿兴鸿，廖勇，姚骏,等(Qu Xinghong,Liao Yong, Yao Jun,etal).永磁同步直驱风力发电系统的并网变流器设计(Design of grid-connected converter for a permanent magnet synchronous direct-drive wind power generation system)[J].电力电子技术(Power Electronics)，2008，42(3)：22-24.

[9] Dai Jingya， Xu Dewei， Wu Bin,etal.Dynamic performance analysis and improvements of a current source converter based PMSM wind energy system[C]// International Conference on Computational Intelligence and Security Workshops, Rhodes, Greece: 2008.

[10]Yazdani A, Iravani R. A neutral-point clamped converter system for direct drive variable-speed wind power unit[J].IEEE Trans on Energy Conversion， 2006，21(2)：596-607.

[11]徐德鸿.电力电子系统建模及控制[M].北京：机械工业出版社，2005.

[12]吴政球，干磊，曾议,等(Wu Zhengqiu，Gan Lei，Zeng Yi,etal).风力发电最大风能追踪综述(Summary of tracking the largest wind energy for wind power generation)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2009，21(4) ：88-93.

[13]姚骏，廖勇，庄凯(Yao Jun，Liao Yong，Zhuang Kai).永磁直驱风电机组的双PWM变换器协调控制策略(Coordinated control strategy of back-to-back PWM converter for permanent magnet direct-driven wind turbine)[J].电力系统自动化(Automation of Electric Power System)，2008，32(20)：88-92,107.

[14]Zou Zongwei，Yu Haisheng，Tang Yuliang.Maximum output power control of PMSM based on energy shaping and PWM control principle[C]∥IEEE International Conference on Automation and Logistics，Qingdao, China：2008.

[15]李燕，梁英(Li Yan，Liang Ying).永磁直驱风电系统电压源型变流技术(Voltage source converter technology in permanent-magnet directly driven wind power system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2010，22(1)：65-70.

[16]马幼捷，杨海珊，周雪松,等(Ma Youjie，Yang Hai-shan，Zhou Xuesong,etal).风电系统的电压稳定性分析(Voltage stability analysis of wind power system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2010，22(3)：22-26.

李军军(1976-)，男，博士研究生，讲师，研究方向为分布式发电。Email:lijunjun8181972@sina. com

吴政球(1963-)，男，博士，教授，博士生导师，研究方向为电力系统分析、电力市场及新能源。Email:zhengqiuwu@163.com

SmallSignalStabilityAnalysisofDirectlyDrivenPermanentMagnetWindPowerSystem

LI Jun-jun1，2， WU Zheng-qiu1， TAN Xun-qiong1

(College of Electrical and Information Engineering, Hunan University,Changsha 410082, China；2.College of Electrical and Information Engineering, Hunan University of Technology,Zhuzhou 412008, China)

Small signal stability mathematical model of directly driven permanent magnet wind power system based on dual PWM converters was established, and the effect on power system stability from parameter variations was researched after wind power system was connected to gird. Some meaningful conclusions were obtained. Maximum power point tracking scheme was applied to wind turbine, and maximum power output was realized in wind power system. Machine side and grid side converters' control structure were studied; then a simulation model was built by Matlab. Time domain analysis were performed in different parameters conditions. Results show system keeps good small signal stability in different parameters conditions, theory analysis correctness was proved, which provides useful theory reference for safe and stable connected operation of direct-driven wind power system.

permanent magnet synchronous generator(PMSG)； PWM converter； small signal stability； maximum power point tracking

TM614

A

1003-8930(2012)05-0049-09

2011-03-28；

2011-04-21

国家自然科学基金资助项目(51077046)