基于风险的低压减载地点选择方法

张志文， 胡 非， 谢洪涛

(1.西南交通大学电气工程学院， 成都 610031； 2.黄石供电公司， 黄石 435000)

基于风险的低压减载地点选择方法

张志文1， 胡 非2， 谢洪涛1

(1.西南交通大学电气工程学院， 成都 610031； 2.黄石供电公司， 黄石 435000)

低压减载是解决电压稳定问题的一种较轻经济的方法之一，低压减载地点的选择是低压减载整定的一项重要内容，选择合适的地点有助于提高系统的电压稳定性。文中分析了PSASP的电压分析模块的数学原理，利用模态分析得到参与因子。结合风险评估的方法，将参与因子计入后果的计算中，通过对风险值的排序来确定低压减载地点。以IEEE39节点系统为例，具体阐述了低压减载地点选择方法的应用，证明了该方法的正确性和有效性。

低压减载； 模态分析； 参与因子； 风险评估

电压失稳是目前电力系统面临的主要威胁之一[1]。为了防止电压崩溃事件的发生，国内外研究并提出了许多方法，低压减载是公认的比较经济且有效的方法之一[2，3]。低压减载地点的选择是低压减载整定的一个重要内容，合适的低压减载地点能够提高低压减载的效率，保证低压减载的有效实施、提高系统稳定性。

很多文献都提出了低压减载地点的选择方法。文献[4]提出了一种灵敏度分析方法，该方法在提出一种电压失稳风险指标的基础上，计算该指标对各节点负荷的灵敏度，并通过灵敏度确定切负荷的地点，节点灵敏度越大，切负荷效果好，应考虑首先切除该节点负荷。文献[5]提出了一种可考虑负荷波动的电压稳定指标，该指标可表示节点静态电压崩溃的概率，从而识别出系统的薄弱节点。文献[6]采用潮流方程雅可比矩阵最小特征值作为电压稳定的指标，通过切负荷将最小特征值增大到给定限值，并计算最小特征值对各节点负荷的灵敏度作为选定切负荷节点的依据。文献[7]认为系统轨迹碰到微分代数方程DAE(differential algebraic equations)系统奇异面对应暂态电压失稳，通过计算奇异面移动的距离对控制参数的灵敏度，选择低压减载的节点。在某种故障下，灵敏度最大的节点即为该故障下的最佳的减载地点。文献[8]提出了一系列风险指标，将大量不确定性因素对电压稳定的影响进行了量化，并且在计算过程中综合考虑了故障表所对应的各种工况，减载地点的风险最小即表示在该点进行低压减载具有最佳功效，通过风险计算来选择切负荷的最佳地点。

电力系统分析综合程序PSASP(power system analysis software package)是中国电力科学研究院自主研发的一套功能强大、使用方便的电力系统分析大型软件包。本文在文献[8]的基础上，对事故的后果的计算方法进行了改进，同时结合PSASP电压稳定分析模块计算参与因子，确定低压减载地点，对IEEE39节点系统进行仿真的结果表明，该方法能快速的确定减载地点，工作量小，可以实现更加合理准确地选择低压减载地点。

1 PSASP的电压稳定分析的数学原理

PSASP的电压分析模块是基于文献[9]所提出的发电机、负荷静态化的雅可比矩阵JS，采用模态分析方法来判别系统的薄弱节点和薄弱区域，相当于近似考虑了系统中与电压稳定性密切关联的动态元件特性。以下为该软件电压稳定分析的数学原理，潮流方程的功率式的修正方程[10，11]为

(1)

式中JS为发电机、负荷静态化的雅可比矩阵。

若令ΔP=0，则可得系统负荷无功功率与节点电压的增量关系为

ΔQ=(L-JM-1N)ΔV=JRΔV

(2)

系统的电压稳定性可由计算JR的特征值和特征向量判定。这就是模态分析判别电压稳定性的基本原理。

计算JR的特征值与特征向量可以得到：

ΔV=ξΛ-1ηΔQ

(3)

或

(4)

式中：Λ=diag{λ1，λ2，…λn}，λ1，λ2，…λn为

JR的特征值；η为JR的左特征向量阵，ηi为η的第i行；ξ为JR的右特征向量阵，ξi为ξ的第i行，ξ=η-1。

由式(4)可得负荷母线k的V-Q灵敏度近似为

(5)

联系到系统关键节点、关键区域的判别问题，引入“母线参与因子”为

Pki=ξkiηik

(6)

这里的Pki决定了λi在母线k对V-Q灵敏度的影响。由于JR近似是一个实对称矩阵，所以其特征值基本为实数。因此，判别系统关键节点和关键区域的问题可以转化为寻找JR的最小特征值及与此最小特征值有关联的各节点的参与因子的最大者。

可分别在初始的稳态运行点和电压稳定的极限点进行模态分析，分别求出各节点对主导电压失稳的模式的参与因子。根据参与因子的大小可以确定系统的薄弱节点和区域。参与因子越大，表明该节点功率发生的变化对电压稳定性的影响越大。通常情况下，初始的稳态运行点对应的电压稳定裕度较高，所以在电压稳定极限点或者重负荷运行方式下进行的模态分析的结果可能更有实际意义。

2 基于风险评估的方法确定低压减载地点

由于低压减载装置中整定的是预先确定的值，如果遇到不同类型的运行方式和故障，整定值可能存在不能适应的问题。为此，本文通过风险评估的方法结合上述所求出的参与因子来确定低压减载的地点。

通常将能导致伤害的灾害可能性和这种伤害的严重程度定义为风险(risk)。根据该定义，风险指标必须包含两个基本的要素，即事件发生的概率和事件造成的后果。因此，本文基于这个两个要素来进行减载地点选择的分析[8，12]。

根据风险的定义，若将减载地点的选择作为一个事件S，Sk表示选择节点k作为减载地点这一事件，则该事件的风险为

Risk(Sk)=P(Sk)×Im(Sk)

(7)

式中：Risk(Sk)为事件Sk的风险，Risk为风险运算符；P(Sk)为事件Sk发生的概率，P为概率运算符；Im(Sk)为事件Sk的后果，Im为后果运算符。

参与因子Pki的大小能直接反映系统节点负荷变化对电压稳定的影响程度，可用来确定系统的薄弱节点和薄弱区域，Pki越大，则表示该节点的电压稳定性越弱。电力系统的风险分析一般都是从经济损失这个角度考虑事故后果，但是这样对事故的影响考虑就不够全面，同时也不能直观地反映系统的安全状态。因此，用经济损失来反映安全状态时全面性、可读性和通用性较差[13]。为解决以上问题，本文将事故产生的后果定义为经济损失和参与因子的商，这样，后果既反映了各节点的电压稳定状态，又考虑了在各节点事件切负荷所带来的经济损失。Sk的后果可以表示为

(8)

式中：Ei为导致当前工况的故障；ΔPk为切掉的负荷量；Fr为单位负荷损失费用；Pk为节点k的初始有功；αik为在该故障下节点k的切负荷比例，αik∈(0,1)；Pki为该点在极限点失稳参与因子。

将式(8)代入式(7)可得

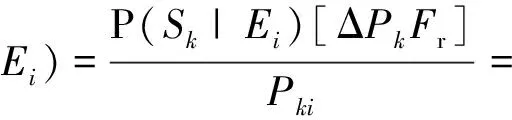
(9)

若假定Ei的各种情况之间是相互独立的，根据全概率公式可得

Risk(Sk)=

(10)

可以对各个负荷节点进行风险计算，具有最小风险的那个节点是最佳的低压减载节点，如果在多个节点进行减载，则可以选择风险最小的前m个节点，使其满足

(11)

式中：α为系统可供切除的负荷占该系统总负荷的比例；Pall为该系统总有功负荷(αik∈(0,1))。

3 确定低压减载地点的步骤

确定低压减载的地点的步骤如下。

步骤1确定配置系统中可切的负荷总量。

低压减载方案设计的第一步是根据当地的负荷水平、负荷构成和不同负荷的重要性水平，综合确定系统电压偏低时当地可供切除的负荷总量。一般情况下安排的切负荷量不应少于该系统负荷的10%～20%。

步骤2在典型过渡方式下，通过PSASP的模态分析模块计算系统各节点的参与因子。

步骤3通过风险评估的方法确定各节点作为减载地点的风险。

通过式(10)来确定各节点减载作为减载地点的风险。此处可以有两种处理的方式，由式(8)可知，可以直接确定ΔPk，不管αik的大小；也可以先确定αik，通过计算得到ΔPk，假定前一种方法为方法1，后一种方法为方法2。这两种处理办法的异同点就在于方法2考虑了节点初始的有功大小，能反映该节点切负荷的能力，初始有功越大，能切掉的负荷就越大，但是这种方法有一个前提就是提前知道各节点的αik，这个数值在实际中根据供电协议和负荷重要程度可以确定。

步骤4确定最终的减载地点。

实际系统中，有时需要在多个节点安装低压减载装置，这时就需要对所有节点的风险进行排序，选择其中风险较小的节点作为减载地点，在已知该系统可切的负荷量的情况下，可以通过式(11)来最终确定减载地点。

4 仿真分析

本文以IEEE 39节点系统为例，系统中的负荷全部是恒功率负荷。通过这个算例阐明上述方法的应用及其有效性。

1)确定可切的负荷总量

在负荷都是恒功率负荷并且缺乏不同负荷的重要性水平的数据的情况下，可以通过参考实际情况和其他文献来确定低压减载的可切负荷总量。文献[2]中确定的最大切负荷量为所有负荷节点负荷的50%，文献[14]结合南方电网当前低压减载配置的具体情况，假定可切负荷总量为总负荷量的40%。以这两篇文献作参照，本文中取可切负荷量为总负荷量的50%。

2)计算系统各节点的参与因子

本文选定典型过渡方式为负荷按等比例、恒功率因数方式增长，增加的负荷由除平衡机外的所有发电机按其容量比进行分担，并在这种情况下对系统进行模态分析。最后可得出所有节点的参与因子。

3)确定各节点作为减载地点的风险

通过式(10)来确定各节点减载作为减载地点的风险。

在计算前，需要做以下分析：

(1)在未确定减载地点之前，可认为每个节点被选作减载地点的概率都是一样的，因此P(Sk|Ei)=1/i，其中i表示负荷节点的个数；

(2)对于Fr，由于每个负荷节点的负荷的重要性，负荷水平和负荷构成都不相同，因此应该根据实际情况来决定每个节点的可切负荷量和单位负荷损失费用，因为本文用的是测试系统，为简单起见，都假定各个节点是一样的，为5 000元/(MW·h)；

(3)对于ΔPk和αik，可作如下假设：若采用方法1，则ΔPk对于每个节点来说都是一样的，都为150 MW(由于负荷节点12的有功只有8.5 MW，与其他负荷相比相差太小，因此该节点在此处不满足条件，但其无功较大，可忽略节点12有功太小这一事实)，若采用方法2，则αik对于每个节点来说都是一样的，都为0.5；

(4)对于P(Ei)，取N-1故障作为预想的意外事件集合，电力系统发生事故的概率基本符合泊松(Poisson)分布[12]，即

(12)

式中：λi为第i个设备的故障率；λj为第j个设备的故障率；t为将要用来评估风险的时间段，h。

本文在同样时间段内进行讨论，假设时间段都为1 h。设备的故障率可以通过设备的使用年限或者实际运行的历史数据等得到，为简便起见，参考文献[12]，可将每个设备的故障率都设为4.58×10-5。

对两种不同的处理方法分别进行计算，可以得到两种情况下各节点的减载风险排序，排序按照风险由小到大的顺序，如表1所示。

4)确定最终的减载地点

由于本文中取可切负荷量为总负荷量的50%，根据式(11)可得到两种方法下分别应该取的节点，如表2所示。

由上表可知，按照方法1确定的低压减载地点和按方法2确定的低压减载地点是一样的，仅仅是顺序有所不同，因此这两种方法都可以用来对低压减载的地点进行选择，在实际系统中，对于负荷的重要性和负荷构成都类似的小范围局部区域可以按照方法1来确定低压减载，而对于系统负荷构成较复杂的地区，则可以按照方法2来整定。

在考虑可切负荷量为总负荷量的50%的条件下，文献[8]所确定的低压减载的地点和采用本文所提出的方法确定的地点是一样的，证明了本文所提出方法的有效性。同时，采用本文所提出的方法，在计算时结合了电力系统分析工具，因此也具有很好的实用性。

表1 两种方法下的母线风险排序

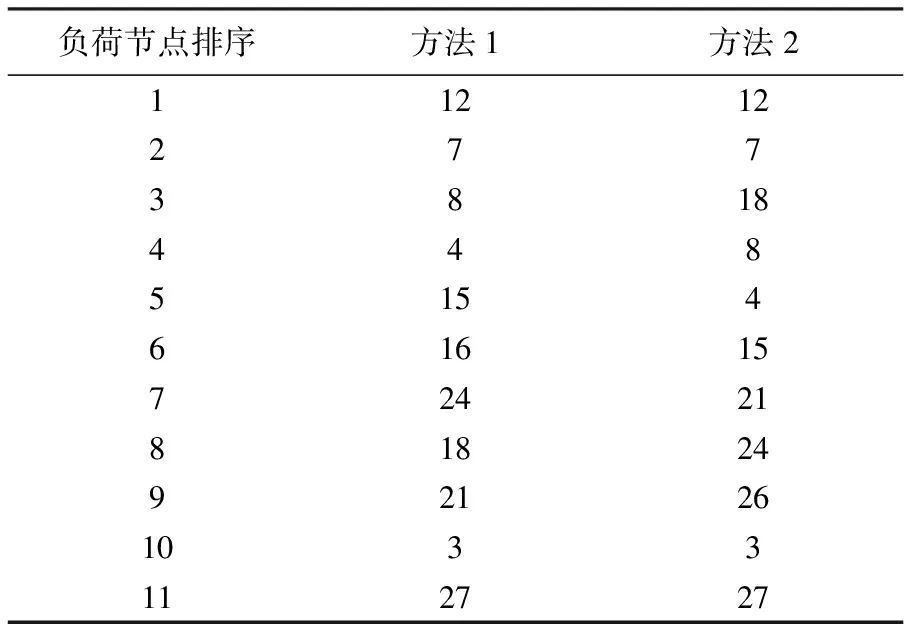
表2 两种方法下选择的切负荷地点

5 结语

本文提出了一种确定低压减载地点的方法。通过结合电力系统分析工具PSASP的模态分析功能，引入风险评估的方法，将各种工况和不确定性因素对电压稳定的影响进行量化，避免因工况的不同而产生的低压减载的整定值不能适应的问题，并通过对各节点风险进行排序来确定低压减载地点。IEEE 39节点系统的仿真验证了该方法工作量小，可以实现合理准确地选择低压减载地点。

[1] 段献忠，何仰赞，陈德树(Duan Xianzhong, He Yangzan, Chen Deshu)．电压崩溃机理探讨(The research for voltage collapse mechanism)[J]．电力系统及其自动化学报(Proceedings of the CSU-EPSA)，1991，3(2)：1-7．

[2] 马世英，易俊，孙华东,等(Ma Shiying, Yi Jun, Sun Huadong ,etal)．电力系统低压减载配置原则及方案(Study on configuration of under-voltage load shedding in power systems)[J]．电力系统自动化(Automation of Electric Power Systems)，2009,33(5):45-49．

[3] Taylor C W. Concepts of undervoltage load shedding for voltage stability[J]. IEEE Trans on Power Delivery, 1992, 7(2): 480-488.

[4] Tuan T Q, Fandino J, Hadjsaid N,etal. Emergency load shedding to avoid risks of voltage instability using indicators[J]. IEEE Trans on Power Systems, 1994, 9(1): 341-351.

[5] 傅旭，王锡凡(Fu Xu, Wang Xifan)．一种新的节点静态电压稳定指标及切负荷算法(A new index of nodal static voltage stability and load shedding method)[J]．电网技术(Power System Technology)，2006,30(10):8-12,17．

[6] Arya L D, Pande V S, Kothari D P. A technique for load-shedding based on voltage stability consideration [J]. International Journal of Electrical Power amp; Energy Systems, 2005, 27(7): 506-517.

[7] 刘斌，陈磊，闵勇(Liu Bin, Chen Lei, Min Yong)．考虑暂态电压稳定的低压减载地点选择(Determination of the location of under-voltage load shedding considering transient voltage stability)[J]．电力系统自动化(Automation of Electric Power Systems)，2008，32(5)：11-14．

[8] 戴剑锋，朱凌志，周双喜，等(Dai Jianfeng, Zhu Lingzhi, Zhou Shuangxi ,etal)．基于风险的低压减载策略问题研究(A risk-based study on under voltage load shedding schemes)[J]．中国电机工程学报(Proceedings of the CSEE)，2006，26(19)：18-22．

[9] 吴涛，王伟胜，王建全，等(Wu Tao,Wang Weisheng, Wang Jianquan，etal)．用计及机组动态时的潮流雅可比阵计算电压稳定极限(Calculation of voltage stability margin by load flow Jacobian matrices and taking account of generator unit dynamics)[J]．电力系统自动化(Automation of Electric Power Systems)，1997，21(4):13-16．

[10]中国电力科学研究院(China Electric Power Research Institute).电压稳定程序使用说明(Voltage stability program instructions)[Z]．北京：中国电力科学研究院(Beijing: China Electric Power Research Institute)，2005．

[11]吴杰康，詹厚剑，齐佳鑫，等(Wu Jiekang,Zhan Houjian,Qi Jiaxin ,etal). 计及STATCOM的电力系统电压稳定特征结构分析(Eigenvalue structure analysis for voltage stability of power system considering Statcom installation) [J]．电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2009，21(6)：1-5．

[12]Wan Hua, McCalley J D, Vittal V. Risk based voltage security assessment [J]. IEEE Trans on Power Systems, 2000, 15(4): 1247-1254.

[13]陈为化，江全元，曹一家，等(Chen Weihua，Jiang Quanyuan，Cao Yijia ,etal)．基于风险理论的复杂电力系统脆弱性评估(Risk-based vulnerability assessment in complex power systems)[J]．电网技术(Power System Technology)，2005，29(4):12-17．

[14]黄镔，赵良，马世英，等(Huang Bin，Zhao Liang，Ma Shiying，etal)．基于PV曲线的低压减载配置方法(Undervoltage load shedding configuration based on PV curve)[J]．电网技术(Power System Technology)，2008，32(23):29-34．

张志文(1985-)，男，硕士研究生，研究方向为电力系统电压稳定。Email:zzw20041130@126.com

胡 非(1985-)，男，硕士，研究方向为电力系统故障诊断。Email:hf_19851005@163.com

谢洪涛(1985-)，男，硕士研究生，研究方向为电力系统故障诊断。Email:bluebird00@163.com

DeterminationoftheLocationforUndervoltageLoadSheddingBasedonRisk

ZHANG Zhi-wen1， HU Fei2， XIE Hong-tao1

(1.College of Electrical Engineering, Southwest Jiaotong University,Chengdu 610031, China;2.The Power Supply Company of Huangshi, Huangshi 435000, China)

Under-voltage load shedding(UVLS)is one of the lowest cost solutions to solve voltage stability problems.Site selection is an important content for UVLS scheme,and choosing suitable sites can improve voltage stability of power system.In this paper,mathematical principles of voltage stability analysis PSASP(power system analysis software package)is analyzed through getting participation factors by modal analysis.Combined with risk assessment in the process of calculating impact,participation factors wound be taken into account.Site selection for UVLS is determined by risk ranking.Taking IEEE 39-bus system for example,the application of site selection for UVLS is expounded.The simulation results show that it's correct and effective.

undervoltage load shedding； modal analysis； participation factor； risk assessment

TM712

A

1003-8930(2012)05-0127-05

2011-05-06；

2011-05-20