基于遗传算法的随机机组组合问题求解

熊高峰， 聂坤凯， 刘喜苹， 蔡振华， 谢上华

(1.湖南大学电气与信息工程学院， 长沙 410082；2.长沙南方职业学院信息技术系， 长沙 410208)

基于遗传算法的随机机组组合问题求解

熊高峰1， 聂坤凯1， 刘喜苹2， 蔡振华1， 谢上华1

(1.湖南大学电气与信息工程学院， 长沙 410082；2.长沙南方职业学院信息技术系， 长沙 410208)

为考虑不确定性负荷对机组组合问题的影响，通过情景分析法引入一系列的情景对不确定性负荷进行建模，建立了随机机组组合问题的数学模型。采用遗传算法求解该优化问题，可自行满足情景簇约束。通过改进初始种群产生方式和变异算子，引进局部搜索算子对遗传算法进行改进，增强了算法的搜索能力。计算结果显示了随机机组组合问题的数学模型和改进遗传算法求解方法的有效性。

情景分析； 负荷不确定性； 随机机组组合问题； 遗传算法

在电力系统中，传统机组组合问题是指在满足负荷等约束条件下合理安排机组的开/停机顺序与出力以使系统发电成本最小。在市场环境下，它是发电商制定竞标策略和电力交易中心编制发电交易计划的重要基础。因此机组组合问题一直是电力系统中的一个重点课题。到目前为止，已提出了从简单的启发式方法到基于复杂数学优化理论以及基于新型人工智能算法的多种最优求解算法。文献[1～4]对这些求解算法进行了概括和总结。

尽管在实际中负荷是不可能精确预测的，但是在传统机组组合问题的建模和求解中，负荷一般作为确定值事先给定，同时，为了应对机组故障和负荷的不确定性，引入了旋转备用约束条件。然而，对于系统调度员来说，确定由开机机组所提供的旋转备用大小是一个难题[5]。备用的选取方法一般有两种[2]：一是以各时段负荷值的10%为备用；二是以所有机组中输出功率上限的最大值为备用。当第二种方法所选择机组的最大输出功率在所有机组中占较大比重时，备用值也随之取较大，与实际情况不相符。系统调度员必须在“高风险-低运行成本”和“低风险-高运行成本”之间进行折中和决策。因此，基于旋转备用的方法没能解决好机组组合问题中机组故障和负荷的不确定性问题。

近年来，随着数学领域中随机优化理论的不断发展和计算机计算能力的飞速提高，考虑不确定性的随机机组组合问题开始得到日益重视。文献[6]于1996年首次采用在不确定条件下处理优化问题的随机规划法[7]来求解随机机组组合问题，为该问题提供了一个崭新的解决思路。该文通过一系列的情景来建模不确定负荷，然后建立了随机机组组合问题的期望值数学模型，最后采用拉格朗日松弛类型的方法对该优化问题进行了分解和求解。随后，国内外众多学者针对随机机组组合问题提出了众多数学模型和求解方法，如两阶段随机规划数学模型[9]、机会约束规划数学模型[10]、改进的拉格朗日松弛类型求解方法[11]以及基于列生成法的求解算法[12]等。文献[13]对随机机组组合问题的数学模型和求解算法进行了概述。

在求解建立在情景分析基础上的随机机组组合问题时，普遍采用拉格朗日松弛类型的求解方法，此类方法处理情景簇约束时较为复杂，而且由于对偶间隙的存在使得该方法难以求得全局最优解。本文采用改进遗传算法求解建立在情景分析基础上的随机机组组合问题，该方法可以自行满足情景簇约束。实例表明本文方法是可行的。

1 随机机组组合问题的期望值数学模型

建立在情景分析基础上、考虑负荷不确定性、并且使用最为普遍的随机机组组合问题的数学模型是期望值数学模型，其优化目标是最小化在所有情景下的期望发电成本。

1.1 不确定性负荷的建模

假定系统调度周期为T个时刻(通常是以1 h为单位)。采用情景分析法建模不确定性负荷时，一般先假定各调度时刻t的总的电力负荷为一个定义在已知概率空间上、且服从有限离散分布的随机变量dt(t=1，2，…，T)，则d=(d1，d2，…，dT)构成一个T维随机向量，d的一个实现值d=(d1，d2，…，dT)称之为情景；然后，采用适当的方法生成一个包含有S个情景ds(s=1，2，…，S)的集合，并确定集合中每个情景在未来的发生概率Ps，所有情景的概率之和为1。理论上没有界定情景数量的依据，为考虑计算时间，通常会根据实际情况选择S的大小。这些情景通常通过图1所示的情景树来描述。如果各调度时刻t的负荷均取最大值，则称此情景为最大负荷情景。

在每一个调度时刻t，情景索引指标s的集合{1，2，…，S}可以被分割成称之为情景簇的互不相交的子集。很显然，每个情景在每个调度时刻只能属于一个情景簇，并且，在调度时刻t的一个情景簇在其随后的调度时刻里将被细分成更多较小的互不相交的情景簇。一般，用B(s，t)表示在调度时刻t情景s是其一个成员的情景簇。

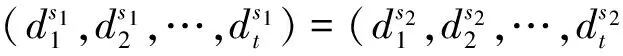
B(s1，t)=B(s2，t)⟹B(s1，τ)=B(s2，τ)

τ=1，2，…，t-1

(1)

根据情景分析中的预测不可能性条件[12，14]，到调度时刻t为止为情景ds1所做的决策必须与到调度时刻t为止为情景ds2所做的决策相同。这是建立在情景分析基础上的随机机组组合问题的数学模型中必须满足的情景簇约束条件。

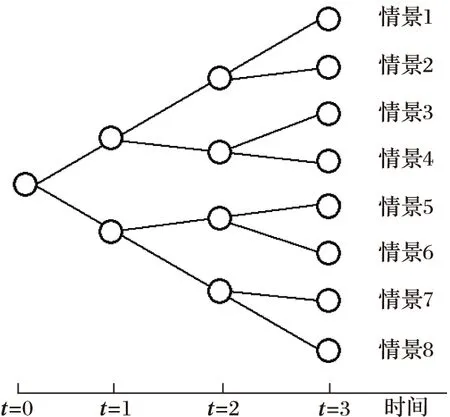
图1 情景树

1.2 期望值数学模型

假定系统中有N台发电机组，则随机机组组合问题的期望值数学模型[6，12]为

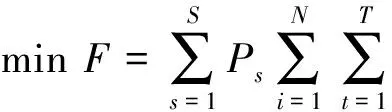
(2)

满足以下约束条件：

(3)

τ=t+1，…，min{t+Li-1，T}

(4)

i=1，…，N；t=2，…，T；s=1，…，S

τ=t+1，…，min{t+li-1，T}

i=1，…，N；t=2，…，T；s=1，…，S

(5)

i=1，…，N；t=1，…，T；s=1，…，S

(6)

i=1，…，N；t=1，…，T；s=1，…，S

(7)

i=1，…，N；t=1，…，T

∀s1，s2∈{1，…，S}，s1≠s2

B(s1，t)=B(s2，t)

(8)

随机期望值数学模型的目标函数是最小化在所有情景下运行成本与启动成本之和的期望值。式(3)表示所有机组的出力之和必须满足情景s下的电力负荷需求。注意，由于采用的是随机数学模型，因此在约束条件中没有必要考虑旋转备用。式(4)和(5)分别为机组的最小开机和最小停机约束条件。式(7)为机组出力的上下限约束条件。式(8)为情景簇约束条件。

随机期望值数学模型是一个包含有S个确定性机组组合问题的大型混合整数非线性规划问题，难以求得其最优解。它是传统机组组合问题数学模型的一个推广。如果情景树只有一个分枝，即只有一个情景，则其就是没有考虑旋转备用的传统机组组合问题的数学模型。

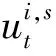
(9)

2 基于遗传算法的求解方法

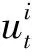
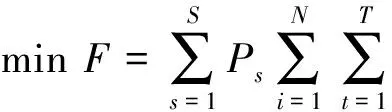
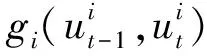
(10)

这一现实情况的反映也促使了GA求解方法的采用。可以采用GA产生一定数量的候选解(调度表)，并根据期望发电成本的大小来衡量各候选解的优劣，再通过一定世代数的选择、交叉和变异等遗传操作最终得到最优解。当采用调度表构成GA中的个体时，可使情景簇约束条件自动得到满足从而减少计算量。因此，本文采用一种改进遗传算法来求解随机机组组合问题。

2.1 编码

采用二进制矩阵编码，染色体由N行T列的二维整型数组构成，数组中第i行t列的元素为机组i在调度时刻t的开停机状态变量的值。

2.2 种群初始化

由于建模不确定性负荷的情景数S一般较大，因此根据测试系统的规模，可以采用动态规划法或者拉格朗日松弛法求解各情景下的确定性机组组合问题，得到S个满足各机组最小开/停机时间约束的可行调度表，由其或者其中一部分构成GA的初始种群，以提高初始种群的质量。

2.3 适应度函数

评估个体的优劣的适应度函数为

(11)

式中，A是一个取决于测试系统规模的常数，用来防止适应值太小，其大小通常与测试系统在调度周期内的最大运行成本保持在同一个数量级或更大。由于在改进GA求解算法中采取了保证个体满足机组最小开/停机时间约束的措施，所以Penalty用于惩罚个体在调度周期内不满足负荷需求时的总缺供电量，惩罚系数为m$/(MW·h)。

2.4 遗传操作

采用赌轮选择法从父代中选择两个个体进行交叉和变异操作。

1)交叉操作

由于窗式交叉和在时间轴上的两点交叉都容易使新生个体不满足机组最小开/停机时间约束，因此采用图2所示的机组间的两点交叉操作。

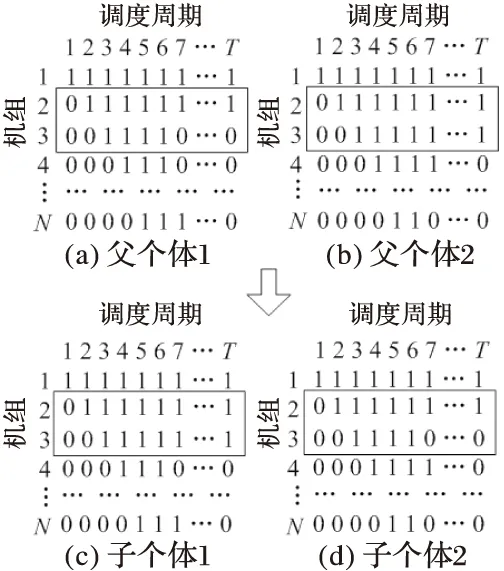
图2 交叉操作

2)变异操作

提出一种能够使变异后的个体满足机组最小开/停机时间约束的新多点变异操作，具体如下。

(1)以变异概率pm在个体中随机选择一台机组i。

(12)

(3)将正负符号交替的整数序列解码转换成该机组在各调度时刻的运行状态。

图3给出一个变异示例，并假定发生变异的机组的最小开/停机时间和初始运行状态分别为3 h/3 h和-3 h，调度周期为24 h。

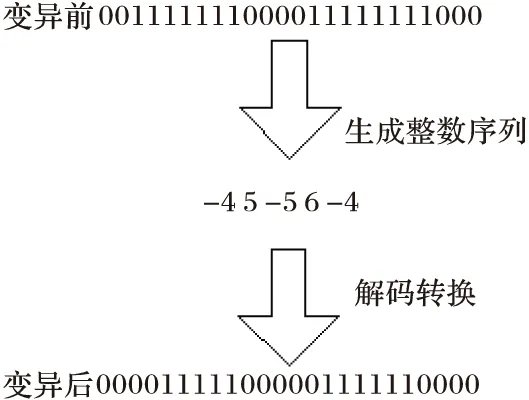
图3 变异算子

2.5 精英策略

为避免每一代的最优个体在进化过程中由于遗传操作而遭到破坏，将其直接复制到下一代中。

2.6 局部搜索

提出一种局部搜索算法并将其应用于每一代的最优个体上，以提高求解质量，具体如下。

(1)在最优个体中依次选择一台机组，将其在调度周期内的运行状态解码成表示其连续开机和连续停机的正负符号交替的整数序列。

(2)从该序列中的首位整数开始，从左至右依次对各整数进行以下操作：

①在满足该机组最小开/停机时间约束条件下，将该整数随机增加或减少1 h，其余整数则在调整次数最小的原则下做相应调整，得到一个新的整数序列。

②将新整数序列解码转换成该机组在各调度时刻的运行状态，并计算改变后个体的适应值。如果优于原最优个体，则将新整数序列取代原整数序列(即新最优个体取代原最优个体)，并在其上进行下一位整数的调整。否则，恢复该机组的原整数序列，并在其上进行下一位整数的调整。

(3)重复步骤(1)和(2)，直至所有机组都被选中一次。

图4给出一个局部搜索示例，假定被选中调整的机组的最小开/停机时间和初始运行状态同上。

2.7 终止条件

采用设定最大进化代数G和在给定进化代数g内最优解没有改善作为终止条件。

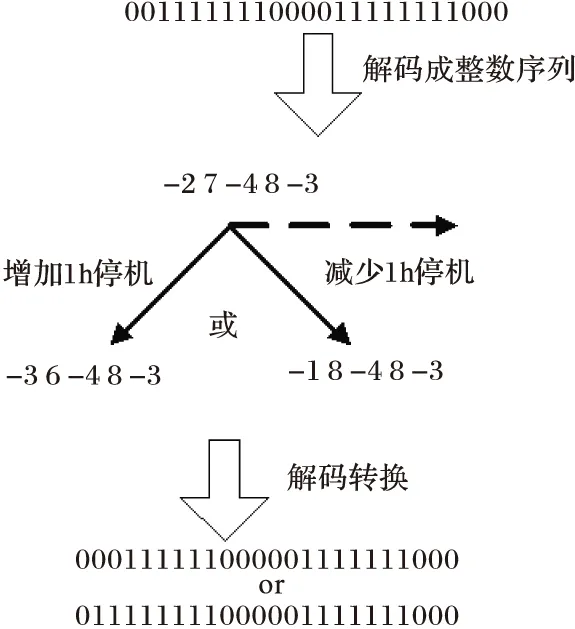
图4 局部搜索示例

3 实例计算

通过在一个N=10，T=24的测试系统上的实例计算来验证文中随机机组组合问题的数学模型与GA求解方法的有效性。测试系统中的机组参数和各调度时刻的负荷Dt详见文献[15]。

如果Dt为精确预测值、不存在误差，则称之为完备负荷信息。但是在现实中负荷是不可能精确预测的。而且，由于受到生产活动及生活习惯的影响，各时段负荷的波动大小不同，一般峰荷波动较大、谷荷波动较小，负荷波动较大时段的负荷预测精度相对较低，文献[6]选择4个阶段负荷波动，生成16个情景。在仿真过程中，多次选择不同的负荷波动时段进行计算。多次试验表明，由于受实例数据本身特点的影响，在选择其他时段作为验证依据时无法得到理想的结果。因此，在建模不确定性负荷、并生成适当数量的情景时，如表1所示，假定在两个峰荷及其附近的6个调度时刻的负荷均有两个等发生概率的可能值，分别为0.9Dt和1.1Dt，其平均值为Dt，其中1.1Dt应对负荷高于Dt的情况，0.9Dt则应对负荷低于Dt的情况。其余调度时刻的负荷为精确预测值，由此产生64个情景。

表1 负荷波动与情景

在GA求解算法中，令P=64，与情景数相同，Pc= 0.5，Pm=0.1，G=500，g=100；不满足负荷需求时，施加的惩罚系数为50 000$/(MW·h)。适应度函数中的常数A=107。由动态规划法求解S个情景下的确定性机组组合问题，产生GA算法中的初始种群。由于GA是一种随机探索求解的优化方法，不能保证每次求解都能得到相同的最优解，因此在求解SUC问题时执行10次GA求解运算并从中得到最优解。表2给出求得的最优调度表。

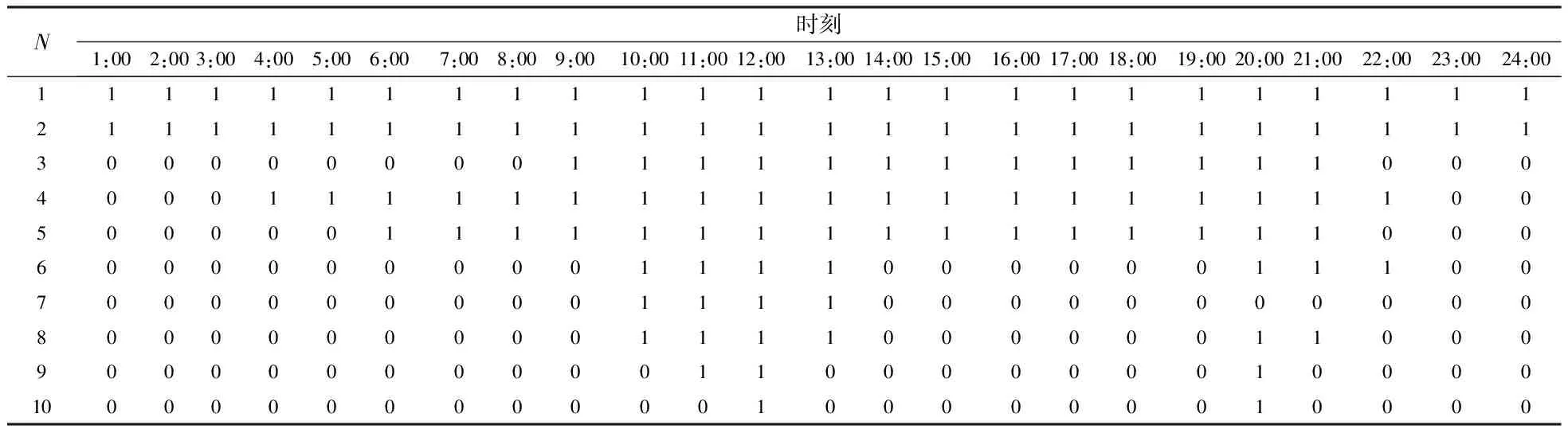
表2 SUC问题的最优调度表

作为比较，表3～表5分别给出由动态规划法求得的最大负荷情景、完备负荷信息以及考虑10%的旋转转备用下确定性机组组合问题的最优调度表。表6给出各最优调度表在各自负荷情景下的发电成本和在64个负荷情景下的期望发电成本。

表3 最大负荷情景下确定性UC问题的最优调度表

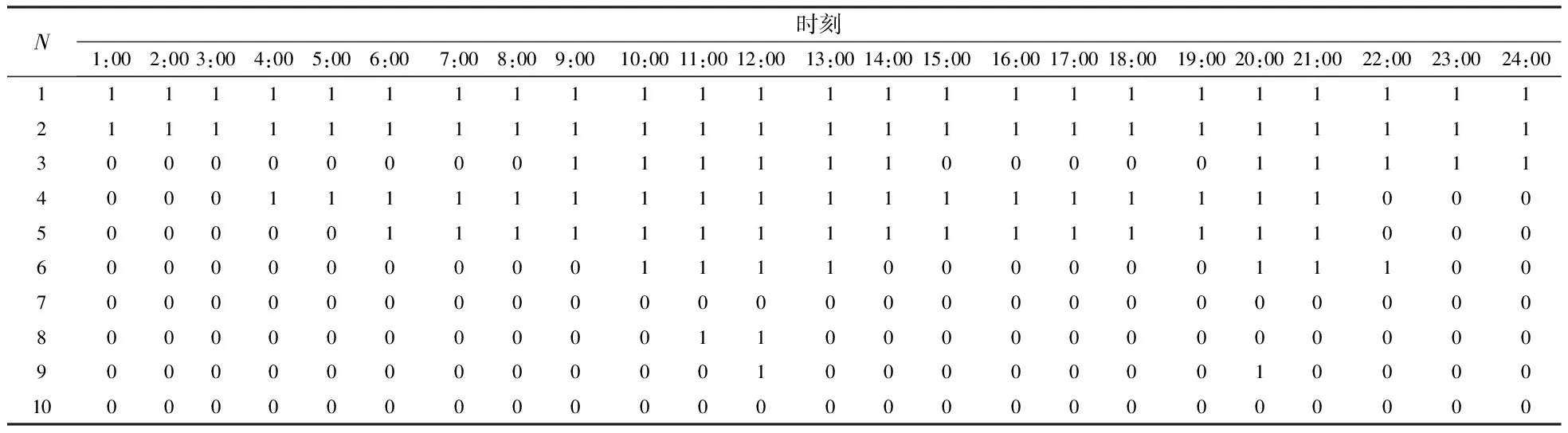
表4 完备负荷信息下确定性UC问题的最优调度表

表5 考虑旋转备用时确定性UC问题的最优调度表

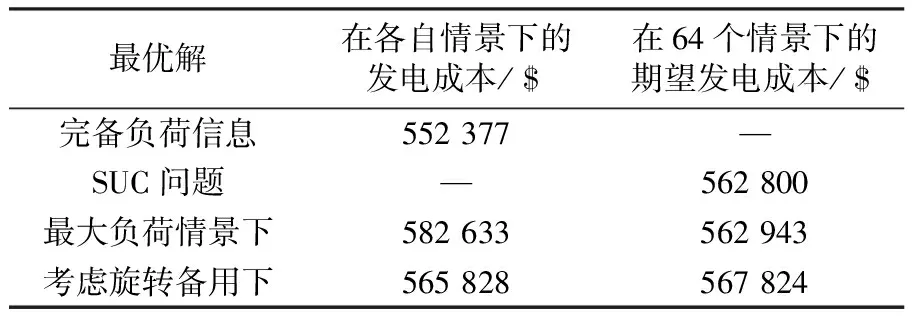
表6 发电成本比较

由计算结果可知，SUC问题的最优解与最大负荷情景下以及考虑旋转备用下的最优解相比，其在64个情景下的平均发电成本分别节省143$和5 024$。同时，由表2中的开机机组所提供的旋转备用小于该时段负荷的10%的时段总计有10个，并集中在负荷波动相对较小、预测精度相对较高的谷兼顾运行行安全性和经济性。另一方面，完备负荷信息下的最优发电成本比SUC问题的最优解在64个情景下的平均发电成本节省10 423$。这是信息精确所带来的利益，也说明加强负荷预测研究、提高预测精度是一项意义重大的工作。

4 结语

采用情景分析法对不确定性负荷进行了建模，建立了考虑负荷不确定性的随机机组组合问题的数学模型。在采用遗传算法求解该最优化问题中，改进了初始种群的产生方法，提出了改进的多点变异操作和局部搜索方法。比较了SUC问题的最优解与完备负荷信息、最大负荷情景以及考虑旋转备用下的最优解。实例计算结果显示SUC问题的数学模型和基于改进遗传算法求解方法的有效性。SUC问题的最优解能够兼顾运行的安全性和经济性。

[1] Sheble G B, Fahd G N. Unit commitment literature synopsis[J]. IEEE Trans on Power Systems, 1994, 9(1): 128-135.

[2] Wood A J, Wollenberg B F.Power Generation, Operation and Control(2nd edition) [M]. New York: John Wiley amp; Sons, 1996.

[3] 陈皓勇, 王锡凡(Chen Haoyong, Wang Xifan). 机组组合问题的优化方法综述(A survey of optimization-based methods for unit commitment)[J]. 电力系统自动化(Automation of Electric Power Systems), 1999, 23(5): 51-56.

[4] Padhy N P. Unit commitment-a bibliographical survey[J]. IEEE Trans on Power Systems, 2004, 19(2): 1196-1205.

[5] Merlin A, Sandrin P.New method for unit commitment at Electricite De France[J]. IEEE Trans on Power Apparatus and Systems, 1983, 102(5): 1218-1225.

[6] Takriti S, Birge J R, Long E. Stochastic model for the unit commitment problem[J]. IEEE Trans on Power Systems, 1996, 11(3): 1497-1508.

[7] Birge J R, Louveaux F. Introduction to Stochastic Programming[M]. New York: Springer-Verlag, 1997.

[8] Carpentier P, Cohen G, Culiolo J-C,etal．Stochastic optimization of unit commitment: a new decomposition framework[J]. IEEE Trans on Power Systems, 1996, 11(2): 1067-1073.

[9] Dentcheva D, Romisch W. Optimal Power Generation under Uncertainty via Stochastic Programming: Numerical Techniques and Engineering Applications [M]. Berlin: Springer-Verlag, 1998.

[10]Ozturk U A, Mazumdar M, Norman B A. A solution to the stochastic unit commitment problem using chance constrained programming[J]. IEEE Trans on Power Systems, 2004, 19(3): 1589-1598.

[11]Takriti S, Birge J R. Using integer programming to refine Lagrangian-based unit commitment solutions[J]. IEEE Trans on Power Systems, 2000, 15(1): 151-156.

[12]Shiina T, Birge J R. Stochastic unit commitment problem[J]. International Transactions in Operational Research, 2002, 1252(11): 117-123.

[13]肖昌育，万仲平，李继生，等(Xiao Changyu, Wan Zhongping, Li Jisheng,etal).机组组合随机模型及其算法简介(The brief introduction of the stochastic unit commitment models and algorithm)[J]. 华中电力(Central China Electric Power), 2005, 18(5): 5-8,12.

[14]Rockafellar R T, Wets Roger J-B. Scenarios and policy aggregation in optimization under uncertainty[J]. Mathematics of Operations Research, 1991, 16(1): 119-147.

[15]Kazarlis S A, Bakirtzis A G, Petridis V. Genetic algorithm solution to the unit commitment problem[J]. IEEE Trans on Power Systems, 1996, 11(1): 83-92.

[16]Valenzuela J， Smith A E. A seeded memetic algorithm for large unit commitment problems[J]. Journal of Heuristics, 2002, 8(2): 173-195.

[17]范宏，韦化(Fan Hong, Wei Hua). 改进遗传算法及其在机组优化组合中的应用(Improved genetic algorithm and its application in unit commitment optimization)[J].电力系统及其自动化学报(Proceeding of the CSU-EPSA), 2004, 16(4): 46-49,63.

熊高峰(1969-)，男，博士，副教授，研究方向为电力系统运行与控制、电力市场。Email:jiaquanx@yahoo.com.cn

聂坤凯(1986-)，男，硕士研究生，研究方向为电力系统经济调度。Email:niekunkai@163.com

刘喜苹(1978-)，女，硕士，讲师，研究方向为数据挖掘、人工智能及其应用。Email:liuviviem808@yahoo.com.cn

GA-basedSolutiontoStochasticUnitCommitmentProblem

XIONG Gao-feng1， NIE Kun-kai1， LIU Xi-ping2， CAI Zhen-hua1， XIE Shang-hua1

(1.College of Electrical and Information Engineering, Hunan University,Changsha 410082， China；2.Department of Information Technology, Changsha Nanfang Vocational College,Changsha 410208， China)

In order to consider the effects of uncertain electric power demand on unit commitment, the uncertainty of electric power demand is modeled by using a set of scenarios, which are introduced by scenario analysis. A mathematical formulation of the expected value model of the stochastic unit commitment (SUC) problem is established. This optimization problem is solved by using a genetic algorithm (GA), which can automatically satisfy the bundle constraints. The performance of the algorithm is improved by introducing a new method to generate the initial population, a new mutation operator, and a local search operator. Based on numerical examples, test results show the feasibility of the mathematical model of the SUC problem and its improved GA-based solution method.

scenario analysis； uncertainty of electric power demand； stochastic unit commitment； genetic algorithm(GA)

TM73

A

1003-8930(2012)05-0093-07

2011-02-16；

2011-04-07