蚁群算法在超高压输电线路故障测距的应用

刘 迅， 黄 纯

(湖南大学电气与信息工程学院， 长沙 410082)

蚁群算法在超高压输电线路故障测距的应用

刘 迅， 黄 纯

(湖南大学电气与信息工程学院， 长沙 410082)

通过对现有输电线路故障测距方法的探讨以及优化算法测距效果的对比分析，提出了一种基于蚁群算法的故障测距方法。该方法基于线路分布参数模型，依据从线路两端分别推算出的故障点电压的幅值相等的原理，列出故障测距方程。引入蚁群算法来求解故障测距方程，并通过相模变换来减少实际线路的不换位和参数不平衡的影响。最后以750 kV超高压输电线路故障测距为例进行仿真，结果表明此算法测距精度高，不需要选择故障类型，不受系统阻抗、过渡电阻、不同步角的影响，有很强的实用价值。

故障测距； 双端非同步测距； 蚁群算法； 分布参数模型； 超高压输电线路

高压输电线路是电力系统的重要组成部分，对电力系统的正常运行影响很大；同时它又是系统中发生故障最多的地方。在输电线路故障发生后，如果能快速、准确地判断线路故障点，就能及早采取措施，减少因停电造成的巨大损失[1]。输电线路故障测距方法一般可分为单端量法、双端量法和行波法。双端量法在原理上可完全消除故障过渡电阻和两端系统阻抗的影响[5]。其中的不需要同步的算法，不要求两端电气量同步，具有更大的工程实用价值。近年来，人工智能化和各种优化算法也被应用于故障测距方程求解中，如模糊理论、遗传算法、最小二乘等等。但这些算法精确度不高，过于复杂和对迭代初值的敏感性，都有待进一步的改善[2，7～10]。蚁群算法ACO(ant colony optimization) 是一种用来在图中寻找优化路径的几率型技术，相比较其他优化算法，具有正反馈、分布式计算和富于建设性的贪婪启发式搜索的特点，已经从离散域扩展到连续域函数的优化问题。同时蚁群算法也是一种并行算法，在解决全局寻优解的复杂问题上具有传统方法难以比拟的独特优越性能，已经在许多函数优化领域得到了广泛的研究和应用。本文提出了一种高压长线路双端故障测距新算法，首先基于分布参数模型依据两端的电压、电流分别推算到故障点的电压的幅值相等的原理，构建故障测距方程。再引入蚁群算法，根据算法理论，将故障测距转化为求一元非线性优化问题。750 kV超高压输电线路的电磁暂态计算程序ATP (alternative transients program)仿真验证了本算法的准确性和实用性。

1 高压长线路模型

在长距离高压输电线路中，按不考虑分布电容的集中参数模型建立的测距算法会有较大的误差。在此采用精确分布参数模型。图1为双端电源的输电线路故障附加网络。

图1 双端电源输电线路故障附加网络

故障点的电压UF，其公式为

(1)

(2)

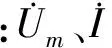
2 三相系统故障测距原理

在实际电力系统中，三相线路之间有互感。在计算之前需要先进行解耦。对于均匀换位的三相输电线路系统，可用对称分量变换。对于非均匀换位，并且参数不平衡的线路，就不能直接使用对称分量变换来进行解藕，要针对实际模型参数的阻抗矩阵和导纳矩阵来求得相模变换矩阵[11]。设S为相模变换矩阵，频域下的相模变换和反变换的关系式为

S-1=QT

(3)

进行模变换后，针对任一模分量，用式(1)和式(2)来表达。

(4)

(5)

式中，j为0、1、2，分别代表相应的0模、1模、2模分量。

考虑到1模分量在任何故障类型下均存在，所以本文采用1模分量系统进行故障测距研究。实际情况下，两端采集到的数据往往是不同步的，但分别由m端和n端求得的故障点电压的幅值必然相等，即

(6)

需要注意的是，由于算法是基于工频正弦模型，而故障录波数据中含有大量的谐波成分，故计算前先要进行滤波。本文中采用滤除衰减的非周期分量的傅氏补偿算法，它速度快，计算简单，精度高，且其滤除衰减周期分量的能力不受衰减非周期分量时间常数大小的限制，使其基波的幅值、相位更加准确。

2 蚁群算法设计

2.1 故障测距优化模型的构建

由式(6)可得

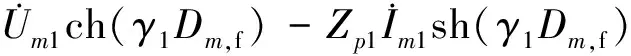
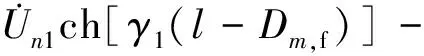
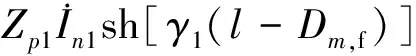
(7)

设

(8)

将Dmf归一化为[0，1]区间的x变量参数，其中1为线路的总长度，即

(9)

代入式(7)，两边平方，得

a2+b2=c2+d2

(10)

由此，测距方程可转化为优化求解问题

(11)

求出x后，故障距离为

Dm，f=xL

2.2 蚁群算法基本原理及算法

对于任何一个自变量在[0，1]范围内的函数最小化问题，可以构造算法模型如下。设问题要求精确到小数点后d位，则自变量x可以由d个十进制数来表示。建立10d+2个城市，共d+2层。其中首末两层只有一个城市，即开始和结束城市。其余d层，每层都有10个城市，分别代表数值0，1，2，3，4，5，6，7，8，9，每层则表示十分位，百分位，千分位…。这些城市中，只有k-1和k(k∈[2，d+2])之间的各个城市之间有连接的通路。图2为求解一元连续函数优化问题的蚁群算法流程[3]。

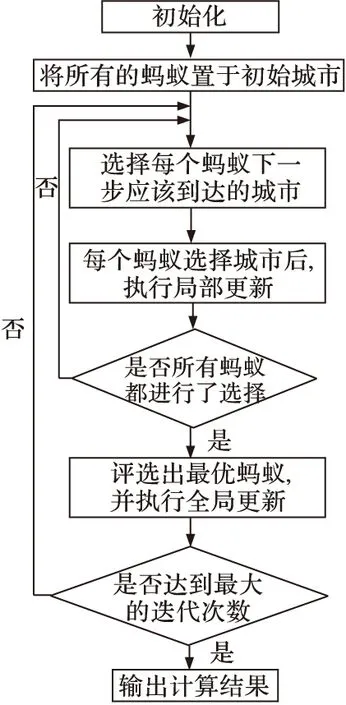
图2 连续函数优化问题的蚁群算法

该算法优化的基本思想是，首先将目标蚂蚁都置于初始城市，并初始化各种参数。然后让每个蚂蚁选择自己下一步应该到达城市，依据一方面是城市之间信息素的多少，另一方面，该算法没有使用确定性的选择策略，而是以一定的概率选择当前最好的路径(即信息素多的路径)，这样可以避免算法限入局部最优并且降低对蚁群初始分布的依赖性。最后当每只蚂蚁选择好路径后，要对每条路径上的信息素进行更新。所有目标蚂蚁都进行一遍选择后，要评选出“最优”蚂蚁，进行信息素的全局更新。

针对图2，每个步骤的具体说明如下。

步骤2让每一只蚂蚁第一步为0，T(n，1)=0(n=1，2，3，…，N0)。

步骤3计算每个蚂蚁下一步要到达的城市，其计算式为

(13)

当每只蚂蚁到达d+1层时，将转移到d+2层的唯一的城市。

所谓伪随机是指根据

(14)

计算选择下一层中每一个城市的概率，然后按此概率用遗传算法中的转盘式选择法确定要选择的城市。

步骤4减弱残留的信息，可以减少下一只蚂蚁选择相同的路径，其公式为

(15)

式中，ρ为0到1的常数，表示路径上残留信息减弱的速度。

步骤5计算蚂蚁n对应的自变量值为

(16)

再计算出每只蚂蚁对应的函数值，并选出其中函数值最小的

nmin=arg min{f(x(n))}

(17)

对这只最优蚂蚁经过的路径进行全局的更新，其更新公式为

i=T(nmin,k-1)

j=T(nmin，k)

(18)

式中：k∈[2，d+2]；α为(0，1)上的常数。

用蚁群算法求解故障距离，能够在搜索过程中避开局部最优解，且对算法的初始群体不敏感；算法中的参数值可以根据实际情况来进行选择，提高了计算精度和算法的实用性。图3为故障距离(理论值为220)随迭代次数的变化趋势。

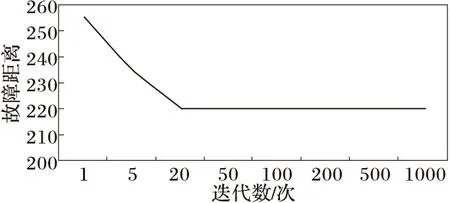
图3 故障距离随迭代次数变化趋势

3 仿真计算

为了验证所提测距算法的正确性，利用电磁暂态仿真程序ATP-EMTP进行仿真，建立750 kV输电线路仿真模型(见图4)。其线路模型参数如下：M侧正序阻抗为0.725+j40.24 Ω，零序阻抗为0.234 2+j13.42 Ω，N侧正序阻抗为2.341+j134.13 Ω，零序阻抗为0.7805+44.71 Ω，线路长度为500 km，线路的单位正序阻抗为0.0127+j0.268 Ω/km，单位零序阻抗为0.272 9+j0.84 Ω/km，单位正序分布电容1.367×10-8F/km，单位零序分布电容9.3×10-9F/km。

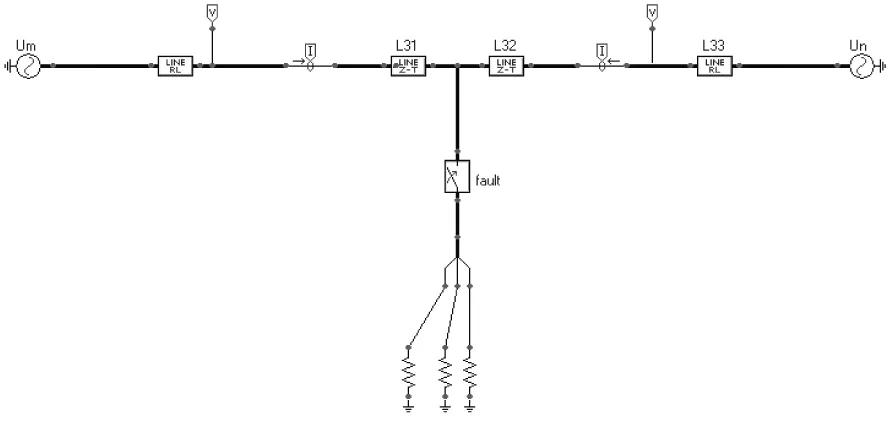
图4 750 kV线路ATP仿真模型

仿真中蚁群算法所用的参数为α=0.8，ρ=0.8，Q0=0.8，τ0=0.01，d=7，N0=20，循环次数为1 000次。

表1给出了本文提出的基于蚁群算法的同一故障点不同故障电阻的故障测距结果。假设实际故障距离为220 km，Em∧En=30°。定义相对误差为(|计算的故障距离-实际的故障距离|/线路总长度)×100%。故障类型分为单相短路(A-G)，两相接地(BC-G)、相间短路(BC)和三相短路(ABC)。表中过渡电阻指相间短路过渡电阻或接地短路的接地电阻。可见故障电阻对算法测距结果影响不大。相对误差受过渡电阻的影响波形如图5所示。图5中，对于单相接地和两相接地，相对误差随过渡电阻略微增大，与蚁群算法30步骤中所选择的伪随机数有关，在可接受的范围内波动。

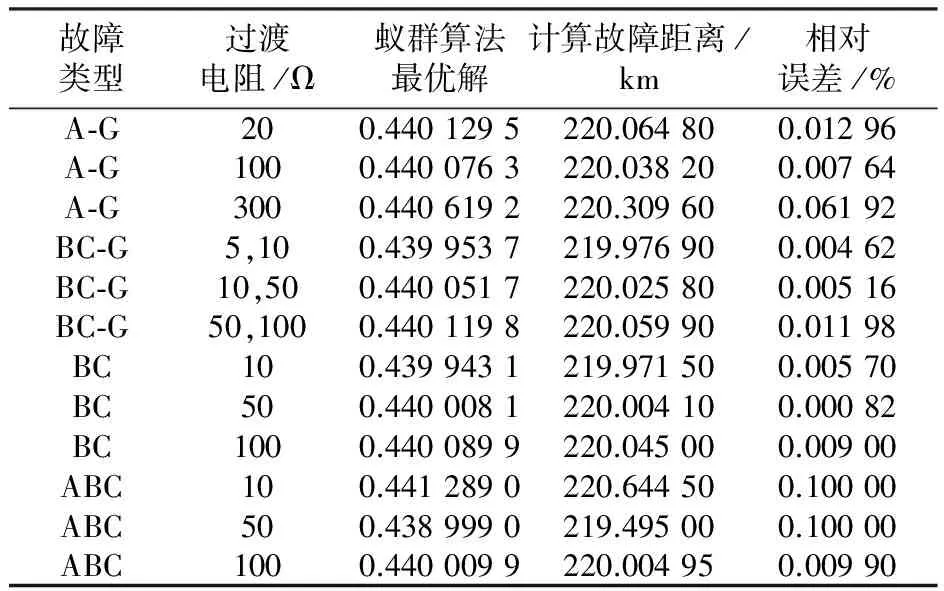
表1 同一故障点不同故障电阻仿真结果

表2给出了算法在同一故障电阻不同故障点的情况下的仿真结果。其中Em∧En=30°，Rg=10 (接地短路接地电阻)，Rf=20 Ω(相间短路过渡电阻)。可见短路距离对算法测距精度影响不大。

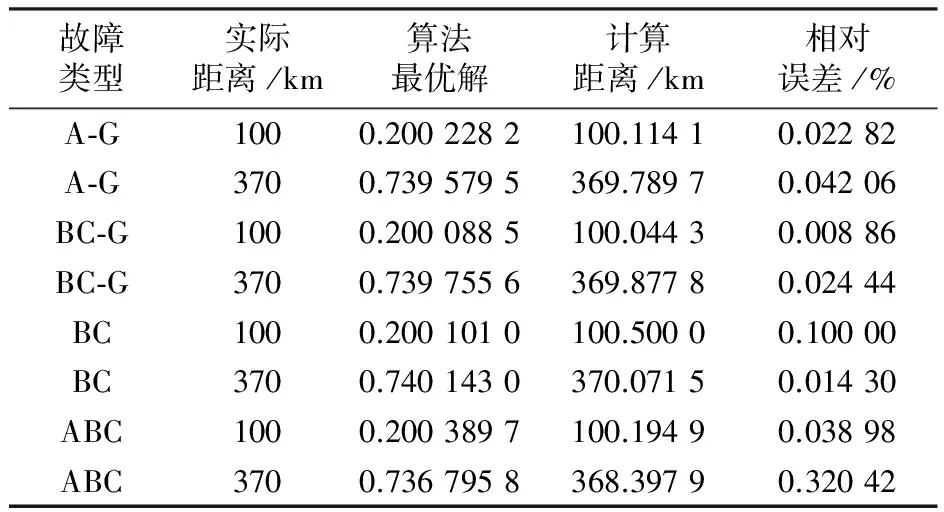
表2 同一故障电阻不同故障点仿真结果

表3给出了算法在线路两端的数据不同步的情况下的仿真结果，不同步也就是说两端的数据不是以共同的参考相量为基础的。假设实际故障距离是220 km，Rg=10 Ω。可见线路两端数据不同步，对此算法的影响不大，相对误差受不同步角的影响波形如图6所示。

'

(a) 单相(A相)接地故障

(b) 两相(BC)接地短路故障

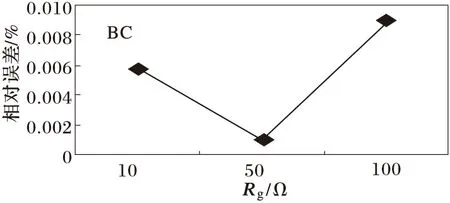
(c) 两相(BC)短路故障

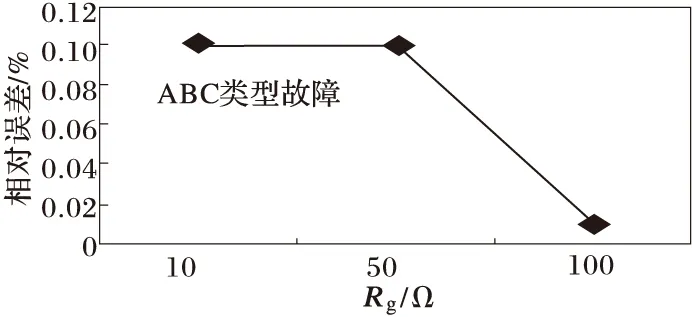
(d) 三相短路故障

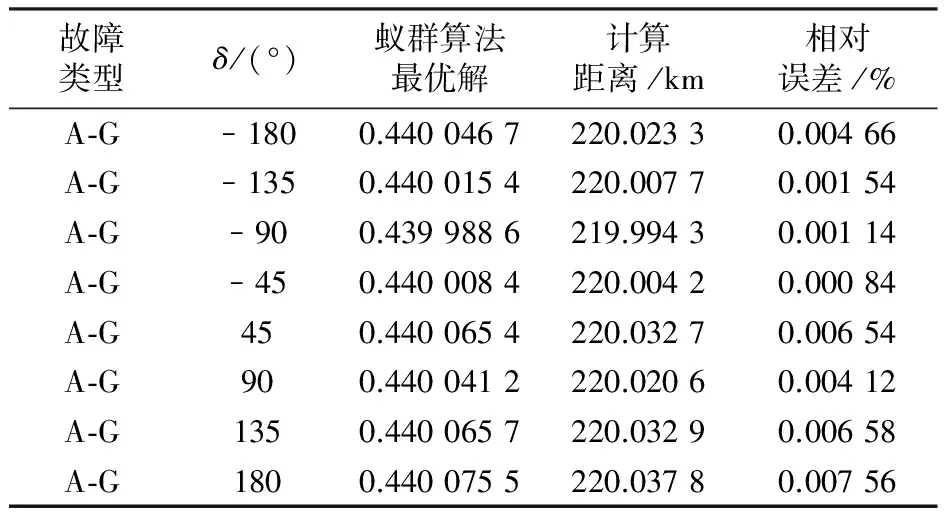
表3 不同步角变化的仿真结果

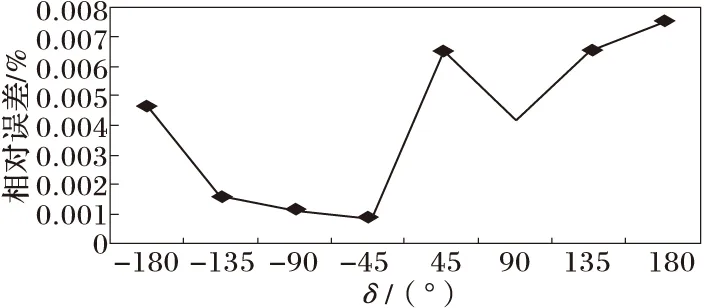
图6 相对误差随不同步角δ的变化趋势

在实际应用中，采集通道有误差和干扰存在，采集得到的电流、电压量和真实的电流电压量会有一定的差距，但对算法的影响不大。由以上仿真结果可以看出，此算法的相对误差控制在0.3%以内，而且当过渡电阻、故障距离和不同步角发生变化时，对测距的影响很小，能达到精确测量故障距离的要求。

4 结语

利用双端电气量来求解高压线路的故障距离，是近年来研究的热点。本文将蚁群算法有效地应用于高压输电线路双端不同步故障测距，并在前人的研究基础上，考虑了算法中的模型、滤波和解藕等多个环节，其主要思想是，按照线路分布参数模型列出含有故障距离的方程组，将解方程组转化为求解最小值的目标函数，再引用蚁群算法来求解此超越方程。通过ATP仿真，验证了此算法具有原理简单，求解方便，速度快，精确度高，不受系统阻抗和过渡电阻的影响，不需要选择故障类型等优点，有很好的工程实用性。

[1] 葛耀中. 新型继电保护和故障测距的原理与技术[M]. 西安: 西安交通大学出版社, 2007.

[2] 梁远升, 王钢, 李海锋(Liang Yuansheng, Wang Gang, Li Haifeng). 基于粒子群-最小二乘混合算法的参数自适应故障测距方法(A parameter adaptive fault location scheme based on the combination of particle swarm optimization algorithm and least squares method)[J].电力系统保护与控制(Power System Protection and Control), 2009, 37(4): 16-22.

[3] 陈烨(Chen Ye). 用于连续函数优化的蚁群算法(Ant colony system for continuous function optimization)[J]. 四川大学学报：工程科学版(Journal of Sichuan University：Engineering Science Edition)，2004,36(6): 117-120.

[4] 陈铮，苏进喜，吴欣荣，等(Chen Zheng,Su Jinxi,Wu Xinrong,etal). 基于分布参数模型的高压输电线路故障测距算法(Fault location algorithm for high voltage transmission line based on distributed parameter)[J].电网技术(Power System Technology)，2000,24(11)：31-33.

[5] 李强，王银乐(Li Qiang,Wang Yinle).高压输电线路的故障测距方法(Fault location methods for high voltage power transmission lines)[J].电力系统保护与控制(Power System Protection and Control)，2009, 37(23): 192-197.

[6] 辛振涛，尚德基，尹项根(Xin Zhentao,Shang Deji, Yin Xianggen). 一种双端测距算法的伪根问题与改进(False root and its improvement of a two-terminal fault location algorithm on transmission line)[J]. 继电器(Relay), 2005, 33(6): 36-45.

[7] 鲁文，徐晨亮，丁孝华，等(Lu Wen, Xu Chenliang, Ding Xiaohua,etal). 一种考虑分布电容的模糊故障测距算法(Fuzzy algorithm for fault location with the distributed capacitor taken into account)[J].电力系统自动化(Automation of Electric Power Systems)，2006, 30(8): 57-60.

[8] 毛鹏，孙雅明，张兆明(Mao Peng, Sun Yaming, Zhang Zhaoning). 具有冗余神经元神经网络模型系统的输电线路故障测距的研究(Study of fault location for high voltage over-head transmission line using neural networks model system with redundant neuron)[J]. 中国电机工程学报(Proceedings of the CSEE)，2000, 20(7): 28-33.

[9] 陈允平，吴夙，龚庆武，等(Chen Yunping, Wu Su, Gong Qingwu,etal). 输电线路故障定位的最小二乘法实现( Least square realization in fault location of transmission line)[J]. 电力系统自动化(Automation of Electric Power Systems)，2001, 25(13): 54-56.

[10]刘涤尘，杜新伟，李媛,等(Liu Dichen, Du Xinwei, Li Yuan,etal). 基于遗传算法的高压长线路双端故障测距研究(Fault location using two-terminal data for HV amp; long transmission line based on genetic algorithm)[J]. 高电压技术(High Voltage Engineering)，2007, 33(3): 21-25.

[11]宋国兵，李森，康小宁,等(Song Goubing, Li Sen, Kang Xiaoning,etal).一种新相模变换矩阵 (A novel phase-mode transformation matrix)[J].电力系统自动化(Automation of Electric Power Systems)，2007,31(14)：57-60.

[12]李一峰，陈平(Li Yifeng, Chen Ping).一种输电线路故障测距新方法 (New method of fault location for transmission lines)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2008,20(4)：125-128.

[13]吴萍，张尧(Wu Ping, Zhang Yao).基于单端电气量的故障测距算法 (Location using one-terminal data for transmission line)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2003,15(4)：5-7,31.

[14]刘东超，李永丽，曾治安(Liu Dongchao, Li Yongli,Zeng Zhi'an).带并联电抗器的双回线故障测距算法研究(Research on accurate fault location algorithm for double circuit transmission line with shunt reactors)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2006,18(2)：5-9,17.

[15]Korres G N, Apostolopoulos C A. Precise fault location algorithm for double-circuit transmission lines using unsynchronized measurements from two anti-parallel ends [J]. IET Generation, Transmission amp; Distribution, 2010, 4(7): 824-835.

刘 迅(1986-)，女，硕士研究生，研究方向为电力系统继电保护。Email:liuxun1986xp@126.com

黄 纯(1966-)，男，教授，博士，研究方向为电力系统自动化、电能质量分析与控制。Email:yellowpure@21cn.com

FaultLocationforEHVTransmissionLineBasedonAntColonyAlgorithm

LIU Xun， HUANG Chun

(College of Electrical and Information Engineering, Hunan University,Changsha 410082, China)

Through analyzing the existing fault location methods and the effect of optimization for transmission line, a method of fault location based on ant colony algorithm is presented. Based on the distributing parameter transmission line model, the fault location function is educed according to the principle that the amplitude of fault point's voltage calculated from the two ends of a line is equal. The ant colony algorithm is introduced to resolve the fault location function optimization problems. To eliminate the effect of untransposed conductors and unbalanced transmission line impedances, phase components are transformed to model components. At last, the simulation based on a 750 kV transmission system model is presented to demonstrate that the algorithm is of high accuracy and not affected by fault type, system impedance, fault resistance, unsynchronized angle. The method has high practical value.

fault location； non-synchronous double-end ranging； ant colony algorithm； distributed parameter model； extra high voltage(EHV )transmission line

TM714

A

1003-8930(2012)05-0132-06

2011-01-24；

2011-04-25