巧用直线参数方程解圆锥曲线中的常见问题
●
(宁波市职业技术教育中心学校 浙江宁波 315040)
巧用直线参数方程解圆锥曲线中的常见问题
●陈健
(宁波市职业技术教育中心学校 浙江宁波 315040)
已知过点P0(x0,y0),倾斜角为θ的直线l的参数方程为

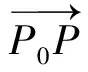
1 巧选t轴原点,解决定性问题
在用直线参数方程解题时,很多人想当然地认为P0(x0,y0)是“定点”,这样在使用时会受到限制.其实“动”与“静”是相对的.在实际解题过程中,可以根据是否能简化运算来灵活选择P0(x0,y0)作为t轴的原点,这时点P0相对于l的任意点就是“定点”.

图1
例1如图1,点P(x0,y0)为抛物线y2=2px(p>0)内部的任意一点,过点P且倾斜角互补的2条直线与抛物线分别交于点A,B,C,D,求证:∠ACD=∠ABD.
证明设直线AB,CD的倾斜角分别为α,β,则直线AB的参数方程为

设此方程的2个根为t1,t2,则

由参数t的几何意义知
同理可得
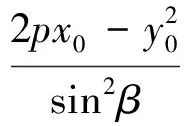
因为直线AB,CD倾斜角互补,所以
sin2α=sin2β.
由式(1),式(2)得
AP·BP=CP·DP,

点评虽然P(x0,y0)为任意点,但是点P为动弦AB与CD所在直线的交点,由于2条弦的位置是固定的,从而点P也是相对固定的,这样就可以选择点P为t轴的原点,设立直线参数方程,巧妙地证明此类定性问题.若结合函数、不等式、三角函数等知识点,此方法还可以适用于解决最值问题.
2 巧用t1+t2=0,解决中点问题
圆锥曲线中有许多涉及中点和对称性的问题,特别是存在性问题,条件比较开放,常常使学生很难入手.若用直线参数方程中参数的几何意义来解,则能顺利切入题目,解法也较为简单.

解设过点B(1,1)的直线参数方程为

t2(2cos2α-sin2α)+2t(2cosα-sinα)-1=0.
(3)
由已知BQ1=BQ2得t1+t2=0,即

解得
sinα=2cosα,
此时式(3)简化为
t2(2cos2α-sin2α)-1=0.
若存在这样的直线m,使得点Q1,Q2关于点B对称,则

而当sinα=2cosα时,

故这样的直线m不存在.
点评例2若按常规方法探讨是否存在,消去参数后计算繁杂.现巧用t1+t2=0,使问题的解法“豁然开朗”,且运算过程较为简洁.
3 巧用d=|t1-t2|,解决弦长问题
直线与圆锥曲线相交形成的“弦长及相关问题”是比较常见的一种题型.此类问题若用一般方法解答,则往往比较复杂且繁琐;若能紧紧抓住直线参数方程中t的几何意义来处理线段长度问题,则能带来极大的方便.

图2

解设直线l的参数方程为
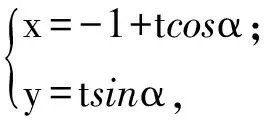
(1+sin2α)t2-2tcosα-1=0.
设点A,B所对的参数为t1,t2,其中
Δ=4cos2α+4(1+sin2α)=8>0,
且
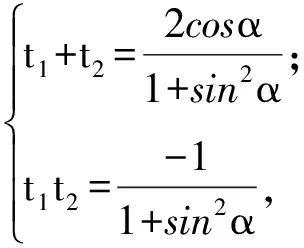


不妨设|AE| ∶|EB|=2 ∶1,则t1=-2t2,从而

t1t2=-2(t1+t2)2,
因此

即
8cos2α=1+sin2α,
解得

从而
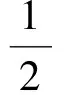
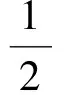
点评直线上有关线段长度的问题,在直角坐标系内一般运用距离公式
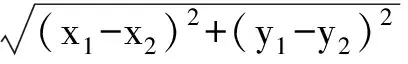
处理.在涉及多条线段且关系复杂时,利用直线的参数方程转化为d=|t1-t2|,可将直角坐标系内的距离“一维化”,从而加快解决此类问题的速度.
4 巧用t的几何意义,解决轨迹问题
圆锥曲线中还有一类问题是非常多见的,它就是“轨迹问题”.要用有限的条件去“捕捉”动点的“万般”变化趋势,特别是在“动点”个数比较多时,要建立关系式是比较困难的.下面介绍怎样用直线参数方程中的几何意义来处理此类问题.

图3
例4如图3,已知直线y=2x+m和双曲线x2-y2=1交于点A,B,P是这条直线上的点,且满足条件|PA|·|PB|=5.当m变化时,求点P的轨迹方程.
解设P(x0,y0),直线y=2x+m的参数方程为
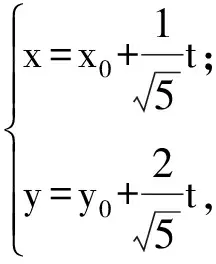


即

将y=2x+m代入x2-y2=1得
3x2+4mx+m2+1=0.
因为直线与双曲线有2个不同的交点,所以
Δ=(4m)2-12(m2+1)>0,
解得


点评巧设P(x0,y0)为t轴原点,设立直线参数方程,虽然此题看似有3个“动点”比较难于解答,但利用t的几何意义“以静制动”,达到了出其不意的解题效果.
总之,运用直线的参数方程解圆锥曲线中的几类题,可使有些看似复杂的问题变得简单.同时这类解题方法思路清晰,可操作性强,学生容易掌握,并可进一步提高学生综合运用代数、几何三角函数知识的能力,从而激发学生的学习热情,拓展学生思维能力.教师在教学过程中能对直线的参数方程作适当的补充与渗透,对学生数学视野的拓宽、探索能力的培养能起到较大的帮助.
[1] 彭耿玲.巧用直线的参数方程解题例说[J].福建中学数学,2009(8):30-32.
[2] 朱斌.新课标下直线标准参数方程的应用(高三)[J].数理化学习,2009(6):47-49.
[3] 欧阳先博.浅谈直线标准式参数方程化二维为一维的解题功能[J].数学通讯,2000(10):10-11.
[4] 高凯.直线的参数方程在圆锥曲线中的应用[J].中学教研(数学).2011(3):29-30.

