基于学习目标的教学设计案例一则——以“椭圆及其标准方程Ⅰ”为例

●

(吴兴高级中学 浙江湖州 313000)

基于学习目标的教学设计案例一则——以“椭圆及其标准方程Ⅰ”为例

●严华峰

(吴兴高级中学 浙江湖州 313000)

1 学习目标的确立

科学、正确的学习目标，能有效地减少课堂教学的随意性、盲目性和模糊性，能提高教学的方向性、针对性和有效性.在确立清晰、具体、有效的学习目标时，首先要明确学习目标确立的依据，即学习目标的来源；其次要对学习目标进行分解，即如何将抽象、概括的目标分解成清晰、具体、有效、可行的学习目标.下面以高中数学选修2-1“圆锥曲线与方程”第2.2.1节“椭圆及其标准方程Ⅰ”为例，阐述学习目标的确立过程.

1.1 确立学习目标的依据及分析

1．1.1 教材分析

(1)本章在教材中的地位与作用：圆锥曲线主要研究圆锥曲线的定义、方程、几何性质，以及它们在实际中的简单应用.它是运用坐标法研究曲线的几何性质的实际演练.

(2)椭圆在教材中的地位与作用：椭圆是3种圆锥曲线中最重要的一种曲线，教材中通过椭圆给出求方程、利用方程讨论几何性质的一般方法，从方法上说，它为我们研究双曲线、抛物线这2种圆锥曲线提供了基本模式和理论基础.

(3)本节在教材中的地位与作用：椭圆的定义和标准方程是椭圆的起始课，也是本章的起始课，椭圆的定义和标准方程是进一步研究椭圆几何性质的基础，同时这节课所体现的思想方法也是后继学习的理论基础.

1.1.2 对课程标准、省学科指导意见、考试说明的解读

学习目标的内涵主要包括学习内容(学什么)、学习程度(学到什么程度)和学习行为(用什么条件学习)这3个方面，因此要确立本节课的学习目标，还需要对课程标准、省学科指导意见、考试说明中的要求作进一步的解读.表1是本节内容学习目标的依据分析表.

表1 学习目标的依据分析表

1.1.3 学情分析

新课程理念下，教学要面向全体学生，每个学校、班级、学生的学情都不一样，甚至不同的教学时段也会影响到同一个学习目标的达成效果，这就要求教师在确立学习目标之前，既要深入地研究教材内容，理解课程标准、省学科教学指导意见、考试说明中的教学目标要求，同时也要立足本校、本班级学生的实际特点，明确学生的具体学情，才能确立具有针对性的学习目标.

(1)学生的知识储备分析：学生已学习了直线和圆的方程，并初步学习了求曲线方程的一般方法和步骤，但学生仍对坐标法解决几何问题存在障碍;

(2)学生的数学能力分析：学生通过几何图形来发现轨迹上点的特征的能力较强(数形结合)，但计算能力较弱，因此在方程的推导中会遇到障碍.

1.2 学习目标的确立

通过解读数学课程标准和省学科教学指导意见，分析教材和学生实情，并考虑近几年涉及该内容的高考试题，“椭圆及其标准方程”这一内容的教学可以分为2个教学课时，第一课时的学习目标如下：

1.2.1 椭圆的定义

(1)通过观察视频、分析日常生活中的实例，对椭圆形成感性认识；

(2)通过探究实验，知道椭圆的轨迹特征，会描述椭圆的定义；

(3)会用椭圆的定义解题.

1.2.2 椭圆的标准方程

(1)通过师生共同推导标准方程，会用“坐标法”求曲线方程，知道椭圆的2种标准方程；

(2)通过学生观察、思考，教师讲解、引导，知道椭圆a,b,c的几何意义，会根据标准方程求a,b,c.

2 基于学习目标的教学设计

学习目标确立后，教师还要设法让学生达成既定的学习目标.为了学习目标的达成，教师应综合考虑各种资源因素，以目标设定教学程序，以目标优化教学过程，以目标创设问题情境，也就是说，要基于学习目标提供相应的教学建议.教学建议通常由3个部分组成：一是课程资源，即为了达成学习目标，教师要提供哪些课程资源；二是为了创造学习条件，教师创设哪些问题情境；三是学生的学习行为条件，即通过什么样的具体的行为条件让学生来学习这个内容并达到相应的程度.以下是基于学习目标的教学设计(以椭圆及其标准方程Ⅰ为例).

环节1情境设置

教学活动：(1)观看视频(卫星运行轨道)，抽象出运动轨迹；(2)举例(生活中椭圆的实例).

教学素材：视频、生活实例.

达成目标：对椭圆形成感性认识.

环节2知识建构

教学活动：观察探究实验(回答下列问题).

问题1在实验中，哪些长度是变化的，哪些是不变的？

问题2能否把不变的量用数学表达式刻画？

问题3可以怎样定义椭圆？

教学素材：实验、教具、问题1～3.

学习评价：

练习1根据椭圆的定义，判断下列动点M的轨迹是否为椭圆:

(1)平面内，到点F1(-2,0),F2(2,0)的距离之和为6的点的轨迹；

(2)平面内，到点F1(-2,0),F2(2,0)的距离之和为4的点的轨迹；

(3)平面内，到点F1(-2,0),F2(2,0)的距离之和为3的点的轨迹.

达成目标：知道椭圆的轨迹特征,会描述椭圆的定义.

环节3知识内化

教学活动：坐标法思想推导椭圆标准方程.

问题4观察椭圆的形状，你认为怎样选取坐标系才能使椭圆的方程简单？

完善学生讨论,师生共同完成椭圆标准方程(2种)的推导.

例1下列方程哪些表示椭圆?若是，判定焦点在什么轴上，并指出a,b的值，写出焦点的坐标：

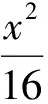
例2求下列椭圆的标准方程：

(2)焦点为F1(0,-3),F2(0,3)，且a=5；

(3)焦点为F1(-2,0),F2(2,0),且过点P(2，3)；

(4)经过点P(-2，0)和Q(0，-3).

教学素材：问题4、例1～例4.

学习评价：

练习3方程x2+ky2=2表示焦点在y轴上的椭圆，则k的取值范围是________.

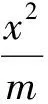
达成目标：知道椭圆的2种标准方程；知道a,b,c的几何意义,会根据标准方程求a,b,c；会用椭圆定义、标准方程解题.

环节4知识归纳

1.知识总结：

(1)椭圆的定义(突出体现“和”、“常数”及“常数的范围”等特征)；

(2)椭圆的标准方程；

(3)a,b,c的几何意义.

2.思想方法总结：坐标法

(师生共同完成，先让学生集体总结、归纳，教师适当引导并补充完善.)

教学素材：教材、学生、教师.

达成目标：能熟练描述定义、标准方程、a,b,c的几何意义.

环节5知识拓展(研究性作业)

(1)用一个平面去截一个圆锥，截口曲线是椭圆，请学生探究：为什么截口曲线是椭圆？

(2)请根据所学的知识，调制一个椭圆规.

教学素材：教材、其他资料.

达成目标：会用椭圆定义解决问题.

学习目标的确立不是凭借随意性和经验性，它应该具有科学性和共性，应该在国家课程标准、省学科指导意见、考试说明及教材的科学分析下，结合本校的具体学情而确立的，并基于目标分解给出教学设计.有了科学、合理的学习目标和教学建议后，可以避免教学的随意性和盲目性，保证课堂教学的方向性和聚焦性，从而提高课堂的有效性.同时，根据学习目标分解而进行的教学设计也是评价教师“教得怎么样”的有效依据，有了这个依据后，在进行课堂教学观察时，可以有针对性地提出指向性的教学改进建议.