珠联璧合 客观题也给力——近3年浙江省数学高考理科卷选择、填空题最后一题评析
●
(余杭高级中学 浙江杭州 311100)
珠联璧合客观题也给力——近3年浙江省数学高考理科卷选择、填空题最后一题评析
●曹凤山
(余杭高级中学 浙江杭州 311100)
数学高考压轴题内涵深厚,往往为大家津津乐道,实际上,一些客观题也同样给力.笔者分析了近3年浙江省数学高考选择题、填空题最后一题可以看出,每道题都是精心打造的上品;而把每年的2道题组合在一起看,更有“珠联璧合、美不胜收”之感.细细品味,相信对高中数学教学、对高考备考会有不少启发.限于篇幅,这里仅以理科试题为例.
1 新而不怪显方向
选择题、填空题的最后一题首先体现在“新”上:试题背景新颖,设问角度巧妙,表达脱俗,注重规避题型套路,给人耳目一新的感觉.试题不仅体现高考考基础、考能力的命题思想,同时,又多植根于教材,对中学数学教学具有很好的引导作用.

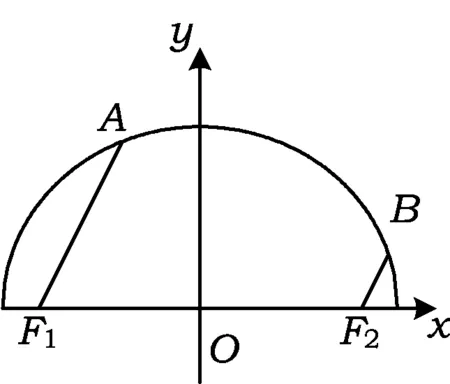
(2011年浙江省数学高考理科试题)
分析该试题与常见的焦点弦问题相似,源于教材又高于教材.试题取自人教A版《数学》选修2-1第48页练习第7题:
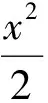
把练习题变题型、改设问、更换条件,更妙的在于背景改编:一个焦点变成2个焦点,直接求解或者转化求解应用的知识、方法可以完全一致.

图1
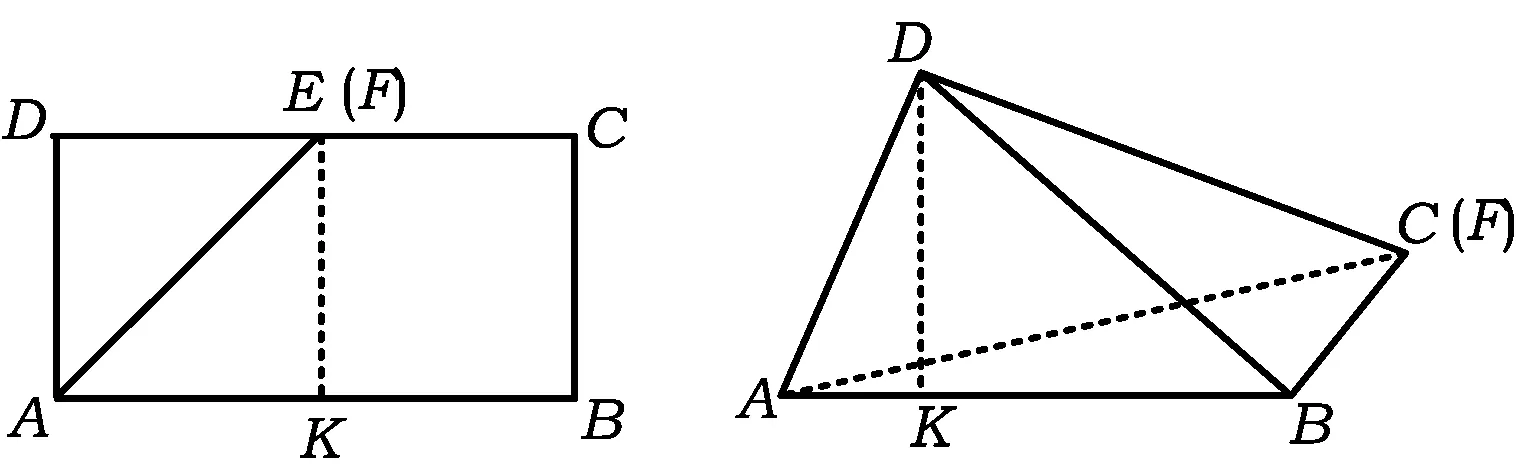
例2如图1所示,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点,现将△AFD沿AF折起,使平面AFD⊥平面ABC,在平面ABD内过点D作DK⊥AB,K为垂足.设AK=t,则t的取值范围是________.
(2009年浙江省数学高考理科试题)
分析该问题以平面图形为基础,通过折叠发展到空间、平面与立体的有机组合,点、线、面、体呈现完整的发展轨迹.在折叠的过程中,点F的位置在变化,体现出“动”的方面,“平面ABD⊥平面ABC,DK⊥AB”是变化中的不变,显示“静”的方面——整个问题恰似唐代大诗人王维在《山居秋暝》中“明月松间照,清泉石上流”的意境,其中空间、平面完美结合,动中有静、静中含动,构成完美的数学问题情境.折叠问题在高中数学学习过程中有接触到,该试题不偏,但往往停留在折叠前、后的“静态”问题情境中,没有发掘变化过程中的精彩.
2 难而不偏重区分
随着命题理论的发展与实践经验的积累,客观题的考查功能也不断得到开发.在难度设计上,试卷由原来的“一题压轴”,逐步过渡到“多题把关”,3种题型体现出3种难度层次,在同一种题型中,难度也阶梯递进,每种题型中都有“把关题”.高考不是每一道题都要有区分度,但一定要有试题体现区分,难度不是实现区分的唯一条件,而是实现区分的重要条件之一.选择、填空最后一题比其前面的试题明显有难度,难以一蹴而就,需要扎实的基本功、一定的数学素养和良好的心理素质,2道题占9分,在其他试题差距不大的情况下,得失的结果也就不言而喻.虽然试题新颖有难度,但不偏不怪,试题设计使基础扎实、能力强的考生可以脱颖而出,有很好的区分度.试题的“不偏”体现在2个方面:一是取材,试题的素材取自高中数学主干知识或具有学科意义的素材,不打“擦边球”,2道试题考查目的不同,相互呼应相得益彰;二是解法,淡化技巧,注重通性通法,每题都可以用基本方法去解决.试题的具体解法这里不再展开.
3 注重阅读考素质
作为把关性试题,不只是单纯考查知识点,而是把知识的考查与能力的考查紧密结合,突出考查学生的学习潜能,其突出表现之一就是对阅读理解能力的考查.
例3对于正实数α,记Mα为满足下述条件的函数f(x)构成的集合:任意x1,x2∈R且x2>x1,有-α(x2-x1) ( ) A.若f(x)∈Mα1,g(x)∈Mα2,则f(x)·g(x)∈Mα1·α2 C.若f(x)∈Mα1,g(x)∈Mα2,则f(x)+g(x)∈Mα1+α2 D.若f(x)∈Mα1,g(x)∈Mα2,且α1>α2,则f(x)-g(x)∈Mα1-α2 (2009年浙江省数学高考理科试题) |f′(x)+g′(x)|≤|f′(x)|+|g′(x)|≤α1+α2, 答案选C. 例4有4位同学在同一天上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”5个项目的测试,每位同学上、下午各测试一个项目,且不重复.若上午不测“握力”项目,下午不测“台阶”项目,其余项目上、下午都各测试一人,则不同的安排方式有________种(用数字作答). (2010年浙江省数学高考理科试题) 分析与例3不同,该试题中没有出现符号,都是文字,很多考生由于“读不懂题”而束手无策.根据数学学科的特点,考查有文字语言、符号语言和图形语言的阅读理解,数学阅读理解是从数学图形、符号、文字等言语载体中提取信息,并进行归纳总结,是动口、动手、动脑的理解加工过程.这类问题的特点是:一普遍渗透,大多客观性把关题中都有这方面的要求;二淡化知识点考查,突出阅读理解能力、数学素养的考查. 图2 立足于通性通法考查是高考的实际,不过在把关题求解的处理上,既要体现这一命题理念,又要体现更高的要求:可以通过“特技”求解. 如例1,可以通过猜想验证求解.如图2所示,猜想点A可能位于比较特殊的位置,如A(0,1),这时yA=5yB=1,从而 图3 图4 如例2,可考虑极限位置.当点F与点E重合时,如图3,△ADF≌△AFK,这时t=1;当点F与点C重合时,如图4,由CB⊥AB,CB⊥DK知 CB⊥平面ADB, 即 CB⊥BD. 需要注意的是,以上“特技”不是建立在题型归纳上的“灵丹妙药”,而是通过灵活深刻的思维,依据问题的具体条件选择的“最短路径”,是问题的“个性解”,是思维能力的表现,是对数学本质深刻理解基础上的判断,是数学素养的体现. 由知识立意到能力立意,体现最充分的是把关题:以知识为载体而不过分注重单纯知识层次上的考查,着眼点在于能力.如例1、例2、例3、例4中分别对空间想象能力、抽象概括能力、运算求解能力、推理论证能力、创新意识、应用意识等进行考查,同时对分类讨论思想、数形结合思想、函数与方程思想、模型化思想等思想方法加以考查,体现“考查基础知识的同时,注重能力考查“的命题原则.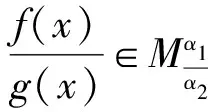
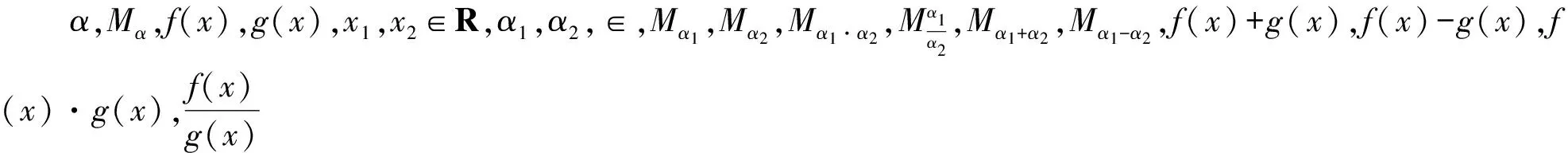
4 通法“特技”相映辉



5 能力立意助选拔

