Lω －空间的ωδ－紧性

艾 姣， 马保国， 吴利飞

（1.陕西省榆林第二实验中学，陕西榆林 718000； 2.延安大学数学与计算机科学学院，陕西延安 716000）

Lω－空间的ωδ－紧性

艾 姣1， 马保国2， 吴利飞1

（1.陕西省榆林第二实验中学，陕西榆林 718000； 2.延安大学数学与计算机科学学院，陕西延安 716000）

在Lω－空间中借助βα－ωδ－开覆盖，定义了Lω－空间的ωδ－紧性，ωδ－基与ωδ－子基，并证明了ωδ－紧性被连续的Zadeh型函数所保持，Tychonoff乘积定理也成立.

Lω－空间；ωδ－开集；βα－ωδ－开覆盖；ωδ－紧性

1 预备知识

在本文中L表示fuzzy格，即具有逆序对合对应“′”的完全分配格.0和1分别表示L中的最小元和最大元.M（L）表示L中全部分子之集，X表示非空集，LX表示X上的全体L－集.0X和1X分别表示LX中的最小元和最大元.M＊（LX）表示LX的全体分子之集.β（α）表示α（α∈L）的最大极小集，β＊（α）＝β（α）∩M（L）表示α的标准极小集，β（A）表示A的最大极小集，β＊（A）＝β（A）∩M＊（LX），记A（a）＝｛x∈X｜a∈β（A（x））｝.其余未说明的概念和记号见参考文献.

定义1.1［1］设X为一个非空集合，ω：LX→LX为满足下列条件的算子：

（i）ω（1X）＝1X；（ii）∀A，B∈LX，A≤B，有ω（A）≤ω（B）；（iii）∀P∈LX，有P≤ω（P）.则称ω为L－fuzzy保序算子.如果A＝ω（A），则称A为LX中的ω集.记Ω＝｛A∈LX｜A＝ω（A）｝，称序对（LX，Ω）为L－fuzzy保序算子空间，简称为Lω－空间.当LX＝2X时，文［2］相应地给出了定义，称为ω－保序算子空间，并记（X，Δ）.

定义1.2［1］设（LX，Ω）是Lω－空间，xα∈M＊（LX），P∈LX.如果存在Q∈Ω使xα≤／Q且P≤Q，则称P为xα的ω－远域，记ωη（xα）为xα的所有ω－远域构成的集族.如果A∈LX且∀P∈ωη（xα），有A≤／P，则称xα为A的ω－附着点.A的所有ω－附着点之并称为A的ω－闭包，记.如果A＝，则称A为LX中的ω－闭集，记ωC（LX）为（LX，Ω）中的所有ω－闭集构成的集族.如果A为ω－闭集，则称A′为ω－开集，记ωO（LX）为（LX，Ω）中的所有ω－开集构成的集族.如果P为ω－闭集且xα≤／P，则称P为xα的ω－闭远域，记ωη－（xα）为xα的所有ω－闭远域构成的集族.

定义1.3［2］设（LX，Ω）是Lω－空间，xα∈M＊（LX），A∈LX.如果∀P∈ωη－（xα）有A≤／ωcl（ωint（P）），则称xα为A的ωδ－附着点.记ωδcl（A）为A的所有ωδ－附着点之并，称为A的ωδ－闭包.如果A＝ωδcl（A），则称A为LX中的ωδ－闭集.如果A为ωδ－闭集，则称A′为ωδ－开集，记ωδC（LX）（ωδO（LX））为（LX，Ω）中的所有ωδ－闭集（ωδ－开集）构成的集族，而记

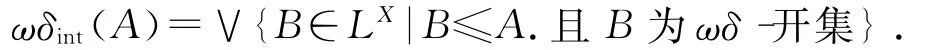
定义1.4设（LX，Ω）是Lω－空间，xα∈M＊（LX），P∈LX，如果P为ωδ－闭集且xα≤／P，则称P为xα的ωδ－闭远域，记ωδη－（xα）为xα的所有ωδ－闭远域构成的集族.如果存在xα的ωδ－闭远域Q使P≤Q，则称P为xα的ωδ－远域，记ωδη（xα）为xα的所有ωδ－远域构成的集族.

定义1.5［3］设L1，L2是两个F格，X与Y是两个非空分明集，p：X→Y是分明映射，q：L1→L2是序同态.则由p，q按下列方式诱导出一个从LX1到LX2的函数

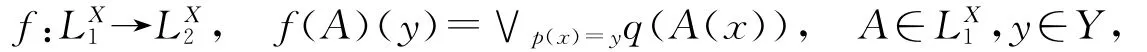
称f为广义Zadeh型函数，并记为f＝pq.

定义1.6［4］设（LX，Ω）是Lω－空间，e∈M＊（LX），ℜ为LX中的一个ω－开集族，即ℜ⊂ωO（LX），如果LX中的每个ω－开集都可表示为ℜ中的若干成员之并，即∀G∈ωO（LX），∃φ⊂ℜ，使得G＝∨B∈φB，则称ℜ为（LX，Ω）中的一个ω－基.若γ⊂ωO（LX）中有限个成员的交的全体构成（LX，Ω）的一个ω－基，则称γ为（LX，Ω）的ω－子基.

定义1.7［5］设（LX，Ω）是Lω－空间，α∈M（L），G∈LX，Φ⊂ωO（LX），若∀x∈X，xα∉β（G′），有xα∈β（∨A∈ΦA），则称Φ是G的一个βα－ω－开覆盖.

定义1.8［5］设（LX，Ω）是Lω－空间，G∈LX，如果∀α∈M（L），G的每个βα－ω－开覆盖都有有限子族构成G的βα－ω－开覆盖，则称G为ω－紧集.若G＝1X，则称（LX，Ω）为ω－紧空间.

引理1.1［6］设L1，L2是完全分配格，f：L1→L2，则下列结论等价：

（i）f保极小集；（ii）f保任意sup.

2 ωδ－紧集

定义2.1 设（LX，Ω）是Lω－空间，α∈M（L），G∈LX，Φ⊂ωδO（LX），若∀x∈X，xα∉β（G′），有xα∈β（∨A∈ΦA），则称Φ是G的一个βα－ωδ－开覆盖.

显然，Φ是G的一个βα－ωδ－开覆盖当且仅当∀x∈X，α∈β（G′（x）∨（∨A∈ΦA（x）））.

定义2.2 设（LX，Ω）是Lω－空间，G∈LX，如果∀α∈M（L），G的每个βα－ωδ－开覆盖都有有限子族构成G的βα－ωδ－开覆盖，则称G为ωδ－紧集.若G＝1X，则称（LX，Ω）为ωδ－紧空间.

3 Tychonoff乘积定理

定义1.7设（LX，Ω）是Lω－空间，e∈M＊（LX），ℜ为LX中的一个ωδ－开集族，即ℜ⊂ωδO（LX），如果LX中的每个ωδ－开集都可表示为ℜ中的若干成员之并，即∀G∈ωδO（LX），∃φ⊂ℜ，使得G＝∨B∈φB，则称ℜ为（LX，Ω）中的一个ωδ－基.若γ⊂ωδO（LX）中有限个成员的交的全体构成（LX，Ω）的一个ωδ－基，则称γ为（LX，Ω）的ωδ－子基.

定理3.1设∀a，b∈L，β（a∧b）＝β（a）∩β（b），ℜ是（LX，Ω）的ωδ－子基，G∈LX.若∀α∈M（L），G的每个由ℜ中的元组成的βα－ωδ－开覆盖都有有限子族构成G的βα－ωδ－开覆盖，则G是ωδ－紧的.

证只须证G的每个βα－ωδ－开覆盖都有有限子族构成G的βα－ωδ－开覆盖.令

［1］陈水利，董长清.L－fuzzy保序算子空间［J］.模糊系统与数学，2002，16（专辑）：36－41.

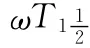
［3］He Wei.Generalized Zadeh function［J］.Fuzzy Sets and Systems，1998，97：381－386.

［4］陈水利.L－fuzzy保序算子空间的ω－基及其性质［J］.江汉石油学院学报，2003，25（3）：143－146.

［5］韩红霞，孟广武.L保序算子空间的ω－紧性［J］.纯粹数学与应用数学，2009，25（2）：390－395.

［6］王戈平.完全分配格上的若辅助序与广义序同态［J］.数学季刊，1998，3（4）：76－83.

ωδ－Compactness inL－order－preserving Operator Spaces

AiJiao1，MaBao－guo2，WuLi－fei1
（1.Yulin Second Experimental Middle School，YuLin 718000China；2.College of mathematics and computer seience，Yanan University，Yanan 716000China）

By means ofβα－ωδ－open cover，the notion ofωδ－compactness，ωδ－base andωδ－subbase inLωspaces is discussed.It is proved thatωδ－compactness is preserved by continuously generalized Zadeh functions and that the Tychonoff Theorem forωδ－compactness is true.

Lωspaces；ωδ－open sets；－ωδ－open cover；ωδ－compactness

O189

A

1672－1454（2012）04－0046－04

2010－02－02