内嵌钢板销式连接胶合木梁短期受力性能

张盛东，范新海，屈文俊

（同济大学 建筑工程系，上海 200092）

随着现代技术的发展与人们生活要求的提高，木结构开始向大跨度、多高层方向发展，其连接节点往往需要较大的刚度并能承受较大的弯矩与剪力，传统连接方式如榫卯连接等已无法满足要求.内嵌钢板销式连接这种新型的节点连接方式能提供给连接节点较高承载力与刚度，已广泛应用于现代木结构节点连接中.文献［1－5］对内嵌单块钢板销式连接节点的破坏模式、承载力计算方法和节点滑移刚度等进行了深入研究，并基于理论和试验结果给出了各种破坏模式下承载力计算公式；文献［6－9］对内嵌单块钢板销式连接节点进行了数值分析；文献［10－11］分析了木材含水率对承载力的影响.徐德良等［12］对内嵌单块钢板螺栓连接节点的受拉性能进行了试验研究.为了使连接节点能获得更高的承载力与刚度，实际工程中一般在较大截面木构件中内嵌两块或三块钢板，如图1所示.2010年上海世博会挪威馆和瑞典馆，木构件间就采用了该种连接方式.Sawata［13］对内嵌多块钢板单销连接顺纹受压节点进行了试验研究，并根据Johansen［14］屈服理论推导了承载力计算公式，结果表明，连接节点的承载力随着钢板数目的增加而增大.国内外对于该种连接的研究主要集中于连接节点的力学性能，而对于内嵌多块钢板销式连接受弯构件力学性能的研究还未见报道.因此本文对内嵌三块钢板销式连接受弯构件的短期受力性能进行了试验研究并推导了承载力与跨中挠度的计算公式.

图1 内嵌钢板销式连接节点示意图Fig.1 Dowel－type timber connections with slotted－in steel plates

1 试验方法

试验共设计两根胶合木梁，截面尺寸为210mm×350mm，通过内嵌三块8mm厚的钢板和16Φ10.6mm钢销连接而成.试件Ⅰ连接节点位于纯弯段，试件Ⅱ连接节点位于弯剪段，试验梁长6000mm，净跨5200mm，如图2所示.

胶合木是由美国花旗松加工而成，实测木材含水率平均值为13%，密度平均值为534kg·m－3；钢销和钢板均采用Q235级钢材，钢销实测直径10.6mm，钢板名义厚度8.0mm，实测厚度7.2mm.

试验采用四点弯曲加载，荷载通过分配梁传递，试验加载示意如图2所示.试验前先对试件进行预加载，正式加载采用分级单调加载，每级荷载5kN，间隔2min，当荷载达到极限荷载50%时，连续均匀单调加载直至试件破坏，每个试件试验总持续时间约为30min.

试验用位移计量测钢板与木构件间的相对滑移（图2a，b中D2～D4）、连接节点处的挠度（图2a，b中D5）、跨中挠度（图2a中D5，图2b中D6）、支座沉降（图2a中D1，D6，图2b中D1，D8）和连接节点对称位置处挠度（图2b中D7）.在试件Ⅰ拼接处（跨越拼接缝）沿高度均匀设置水平方向位移计，量测跨中截面变形沿截面高度分布情况；在试件Ⅱ跨中截面沿高度均匀设置应变片，量测跨中截面应变沿高度分布情况.所有量测数据均由静态应变测量系统同步采集.

2 试验结果及分析

2.1 试验现象

试件Ⅰ，在加载至32kN时，节点处发出明显的“吱嘎”声响，并在接缝处木构件两端的上边缘第二行钢销连线的端部产生水平裂缝，节点接缝处梁底最大开口宽度为7mm；随着荷载的增加，裂缝沿着第二行钢销的连线水平开展，第一行钢销的连线处也逐渐产生水平裂缝，节点接缝处开口继续增大；在极限荷载58kN时，在第一行和第二行钢销的连线位置发生顺纹劈裂破坏，接缝处梁底最大开口宽度达15mm，顺纹劈裂长度达497mm，如图3a所示.

试件Ⅱ，在加载至35kN时，节点处发出明显的“吱嘎”声响，并在靠近加载段木构件的上边缘第一行钢销连线的端部产生水平裂缝，节点接缝处梁底最大开口宽度为6mm；随着荷载的增加，裂缝沿着第一行钢销的连线水平开展，接缝处开口宽度继续增大；在极限荷载70kN时，在第一行钢销连线位置发生顺纹劈裂破坏，梁底接缝最大开口宽度达15mm，顺纹劈裂长度达506mm，如图3b所示.

两个试件最终均由于连接处破坏而破坏，试件的其余部分几乎没有损伤的迹象.

为了更好地了解节点的受力情况和破坏机理，在试验结束后，将节点锯开，主要观察钢销变形和钢销处木材承压变形，试件Ⅰ试验后钢销变形如图4所示，试件Ⅱ钢销变形情况与试件Ⅰ类似.

试件在破坏时，节点处下两行钢销发生不同程度弯曲变形，并形成了塑性铰，钢销处的木材发生承压变形，其破坏模式类似于Sawata［13］给出的内嵌三块钢板单销连接节点屈服破坏模式中Ⅱ和Ⅴ；上两行钢销未发生明显变形，钢销处的木材也没有发生明显承压变形.连接节点的破坏机理为：连接位于纯弯段时，受压区压力主要由木材承担，受拉区拉力由钢板、钢销与木材共同承担；连接位于弯剪段时，竖向剪力由钢板、钢销与木材共同承担，其余类似于连接位于纯弯段.当荷载达到一定值后，最下一行钢销首先屈服并形成塑性铰，钢销处木材达到承压强度，当荷载继续增大，受压区木材达到抗压强度后破坏.

2.2 荷载-跨中挠度曲线

图5给出了试件Ⅰ与试件Ⅱ的荷载－跨中挠度曲线.从图5可以看出，在加载初期，荷载和跨中挠度关系基本呈线性变化.随着加载的进行，荷载增长缓慢而挠度增长较快，斜率逐渐减少，这主要由于钢销的弯曲变形并逐渐形成塑性铰.同时也可以看出，试件Ⅱ的极限承载力显著大于试件Ⅰ，且在相同荷载作用下试件Ⅱ跨中挠度小于试件Ⅰ.若不考虑不确定性，连接节点构造若相同，则其承载力基本相同，连接节点处承载力由弯矩起控制作用，由于弯剪段弯矩小于纯弯段，故得到上述结果.在达到极限荷载时，试件Ⅱ荷载迅速下降，而挠度几乎维持不变；试件Ⅰ荷载－挠度曲线具有一段缓慢下降段，荷载缓慢降低，挠度逐渐增大，说明试件Ⅰ较试件Ⅱ具有较好的延性.试验表明，构件受力由连接节点的性能与位置控制.

图5 荷载－跨中挠度曲线Fig.5 Curves of load and mid－span displacement

2.3 跨中节点相对位移和截面应变分析

图6a给出了试件Ⅰ跨中连接接缝处沿截面高度的相对位移分布，图6b给出了试件Ⅱ跨中截面处沿截面高度的水平应变分布.

从图6a可以看出，在加载过程中，试件Ⅰ在节点拼接处的相对位移沿截面高度基本呈线性分布，符合平截面假定；从图6b可以看出，试件Ⅱ弯曲段的跨中截面应变沿截面高度基本呈线性分布，也符合平截面假定.

3 承载力及挠度计算

本文计算采用的基本假定：① 变形满足平截面假定；② 木材的销槽承压与钢销的受力变形为理想弹塑性；③连接构件的破坏模式是最下一行钢销先屈服破坏，最终受压区边缘木材达到抗压强度fc而发生破坏.

3.1 承载力计算

3.1.1 连接节点位于纯弯段

图7给出了连接节点位于纯弯段时连接节点处假定的横截面受力分布情况.

图7 连接节点处木梁横截面受力分布情况Fig.7 The force distribution in the connections cross section of beams

假设木材受压区高度为hc，则第i行钢销受力为

由力矩平衡，得极限弯矩Mu

式中：Ti为第i行钢销极限承载力；T1＝nrPu，0，其中nr为钢销列数，Pu，0为内嵌三块钢板单销连接节点顺纹承载力［13］；C为受压区压力合力；s为钢销行距；fc为木材顺纹抗压强度；h0为最下面一行钢销至受压最边缘木纤维距离；b为木梁宽度；h为木梁高度；t为钢板厚度；n＝（h0－hc）／s＋1.

3.1.2 连接节点位于弯剪段

在纯剪力V单独作用下，假定剪力V被均匀地分配到每个销连接件上，纯剪连接极限承载力Vu为

当在弯矩M和剪力V共同作用下时，本文采用Jensen［15］给出硬木销连接节点在弯矩M 和剪力V共同作用下的破坏准则

式中：Pu，90为内嵌三块钢板单销连接节点横纹承载力［13］；N 为拼缝一侧销总数；Mu为纯弯极限承载力，由公式（1）得到；Vu为横纹纯剪极限承载力，由公式（2）得到.

3.2 挠度的计算

（1）弯矩作用下连接端部转角θM

图8a所示在弯矩作用下连接端部转角θM为

式中：δ为底部起第一行钢销处相对变形的一半.节点端部力平衡

节点端部弯矩平衡

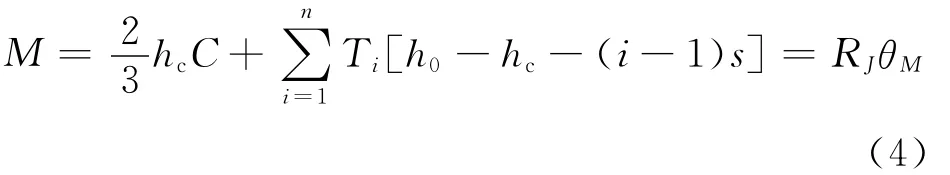
由公式（3），（4）可求得节点转动RJ

式中：KM为弯矩作用下连接节点的滑移模量.

（2）剪力V作用下连接端部转角θV

图8b所示在剪力V作用下连接端部转角θV为

式中：Δ为剪切变形，g为销群形心主界面的距离.

EC5［16］给出了对于预钻孔的单个销每剪切面的滑移模量Kser计算公式

则内嵌三块钢板销式连接弯矩作用下的滑移模量KM为

内嵌三块钢板销式连接剪力作用下的滑移模量KV为

式中：ρk为木材密度；d为钢销直径；ns为钢销行数.

对于内嵌三块钢板销式连接木梁跨中挠度d0

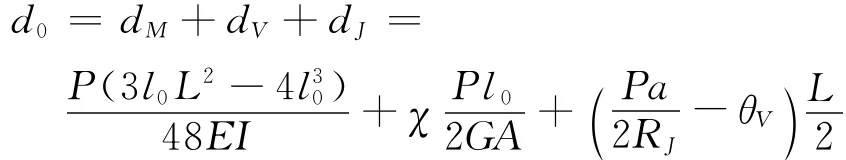
式中：dM为弯矩引起挠度值，dM＝P（3l0L2－4l30）／（48EI），其中L为梁跨度，l0为剪跨长度，E为胶合木的弹性模量，I为截面惯性矩；dV为剪力引起挠度值，dV＝χPl0／（2GA），其中χ为剪力不均匀系数，矩形截面χ＝1.2，G为胶合木剪切模量，A为截面面积；dJ为节点转动引起挠度值，dJ＝（Pa／2RJ－θV）L／2，其中a为连接节点距支座距离.

3.3 公式的验证

承载力和跨中挠度验算时，木材的力学性质按照胶合木强度等级GL36［17］.从表1中可以看出，承载力和跨中挠度的理论计算值与试验值吻合.

表1 理论计算结果与试验结果比较Tab.1 Comparison of the calculated results and the test results

4 结论

（1）本次试验内嵌钢板销式连接胶合木梁的破坏始于连接节点的破坏，试件其余部分几乎完好，连接节点是内嵌钢板销式连接构件的薄弱部位.

（2）纯弯段的胶合木梁截面应变和内嵌钢板销式连接胶合木梁的连接节点接缝处相对位移沿截面高度分布符合平截面假定.

（3）内嵌钢板销式连接胶合木梁的承载力与连接节点的位置有关，连接节点位于弯剪段的木梁极限承载力大于连接节点位于纯弯段的木梁承载力.

（4）根据试验观察到的构件受力特点，并在国外相关研究基础上，推导了内嵌钢板销式连接胶合木梁的承载力与挠度计算公式，理论计算结果与试验结果符合较好.

［1］Jorissen A.Double shear timber connections with dowel type fasteners［D］.Delft：Delft University，1998.

［2］Quenneville J H P，Mohammad M.On the failure modes and strength of steel－wood－steel bolted timber connections loaded parallel－to－grain［J］.Canadian Journal of Civil Engineering，2000，27（4）：761.

［3］Gattesco N，Toffolo I.Experimental study on multiple－bolt steel－to－timber tension joints［J］. Materials ＆ Structures，2004，37（2）：129.

［4］Lantos G.Load distribution in a row of fasteners subjected to lateral load［J］.Journal of Wood Science，1969，1（3）：129.

［5］Guan Z W，Rodd P D.Hollow steel dowels：a new application in semi－rigid timber connections［J］.Engineering Structures，2001，23（1）：110.

［6］Xu B H，Bouchaïr A，Taazount M，et al.Numerical and experimental analyses of multiple－dowel steel－to－timber joints in tension perpendicular to grain［J］.Engineering Structures，2009，31（10）：2357.

［7］Moses D M，Prion H G L.A three－dimensional model for bolted connections in wood［J］.Canadian Journal of Civil Engineering，2003，30（3）：555.

［8］Patton－Mallory M，Pellicane P J，Smith F W.Qualitative assessment of failure in bolted connections：maximum stress criterion［J］.Journal of Testing and Evaluation，1998，26（5）：489.

［9］Patton－Mallory M，Pellicane P J，Smith F W.Qualitative assessment of failure in bolted connections：Tsai－Wu stress criterion［J］.Journal of Testing and Evaluation，1998，26（5）：497.

［10］Sjödin J，Johansson C－J.Influence of initial moisture induced stresses in multiple steel－to－timber dowel joints［J］.European Journal of Wood and Wood Products，2007，65（1）：71.

［11］Rammer D R，Winistorfer S G.Effect of moisture content on dowel－bearing strength［J］.Wood and Fiber Science，2001，33（1）：126.

［12］徐德良，刘伟庆，杨会峰，等.木材－钢填板螺栓连接的承载能力试验研究［J］.南京工业大学学报：自然科学版，2009，31（1）：87.XU Deliang， LIU Weiqing， YANG Huifeng， et al.Experimental study on bearing capacity of bolted wood－steelwood connections in timber structure［J］.Journal of Nanjing University of Technology：Natural Science Edition，2009，31（1）：87.

［13］Sawata K，Sasaki T，Kanetaka S.Estimation of shear strength of dowel－type timber connections with multiple slotted－in steel plates by European yield theory［J］.Wood Science，2006，52（6）：496.

［14］Johansen K W.Theory of timber connections.Publication 9［R］.Bern：International Association for Bridge and Structural Engineering，1949.

［15］Jensen J L，Gustafsson P－J.Shear strength of beam splice joints with glued－in rods［J］. Wood Science，2004，50（2）：123.

［16］BSCEN.EN1995－1－1：2004.Eurocode 5—Design of timber structures.part 1－1：general rules and rules for buildings［S］.UK：BSI，2004.

［17］Technical Commitee B1525.BSEN1194： 1999. Timber structural－glued laminated timber－Strength classes and determination of characteristic values［S］.UK：BSI，1999.