黏土中水平受荷桩基计算方法

王国粹，杨 敏

（同济大学 岩土及地下结构教育部重点实验室，上海 200092）

工程中的桩基常受到侧向荷载的作用，如高层建筑桩基受到上部结构传递的风荷载和地震荷载，电力传输塔受到输电线的侧向拉力，桥梁墩台受到交通荷载，港口结构物受到系泊船只的拉力或撞击力，海洋平台基础受到波浪或水流施加的侧向荷载等.目前，侧向荷载对桩基的影响受到广泛的重视.

在学术界和工程界，分析水平受荷桩常用的方法是p－y曲线法，y表示研究点处桩体的水平位移，p表示研究点处桩周土体的水平抗力，土体极限水平抗力用pu表示.将桩简化为一系列连续的梁单元，桩周土体简化为单元节点处的非线性弹簧，不同深度处土弹簧的特性用不同的p－y曲线来代表，如图1所示.

图1 桩身各点的p－y曲线Fig.1 p－ycurves of individual points on the pile

求解下面侧向受荷桩的基本微分方程，即可得到桩身各点的变形

式中：x为地面以下的深度；y为桩身水平位移；EI为桩截面抗弯刚度，其中E为弹性模量，I为材料横截面对弯曲中性轴的惯性矩；k为x深度处p－y曲线的割线模量，k＝－p／y.

上述方程的计算结果主要取决于p－y曲线的形式.对于黏土中水平受荷桩，美国石油协会规范（API）和挪威船级社海洋风机结构设计规范（DNV－OS－J101），都规定采用现场试桩来得到实测的p－y曲线，若没有实测曲线，可采用Matlock的水下软黏土p－y曲线进行计算.此后，我国《海上固定平台规划设计和建造的推荐做法——工作应力设计法》（SY／T10030－2004）和《港口工程桩基规范》（JTJ254－98）也引入了上述规定.

本文对现有的实测p－y曲线模型进行总结和分析，建议采用理想弹塑性p－y曲线计算水平受荷桩.理想弹塑性模型意义明确，形式简单，参数较少.通过选取合理参数，可得到与实测相近的结果.因此，可以代替实测p－y曲线方法广泛应用于工程运算.

1 现有的p-y曲线模型

自从 McClelland和Focht［1］提出p－y曲线方法以来，对黏土中水平受荷桩p－y曲线的研究主要依靠现场试验.首先，通过水平载荷试验，得到试桩各截面中性轴两侧的应变，并换算得到截面弯矩M.其后，用曲线拟合法得到弯矩的连续函数，并经过微积分运算，确定桩身变形和地基反力分布.最后，绘制各深度处的p－y关系曲线.

利用实测p－y曲线求解侧向受荷桩的基本方程得到的变形和内力，往往与实测值相吻合.实际工程中，当在无法测得p－y曲线时，通常选用已有的p－y曲线模型进行计算.

1.1 现有的p-y曲线模型

许多学者采用上述方法得到了实测p－y曲线模型.Matlock［2］基于直径324mm的钢管桩试验提出了软黏土p－y曲线；Reese［3］提出了水下硬黏土的p－y曲线；Reese和 Welch［4］提出无地下水硬黏土p－y曲线；Sullivan［5］综合上述曲线提出了p－y曲线统一法；Dunnavant和 O’Neil［6］提出了水下超固结黏土p－y曲线；王惠初和曹子爱［7］通过水下饱和黏土中的横向受荷桩现场试验，提出了双曲线形式的p－y曲线；章连洋和陈竹昌［8］结合室内模型试验结果，对Matlock软黏土p－y曲线进行了改进.

1.2 算例分析

以Matlock报道的钢管桩水平静载试验为例［2］，采用上述p－y曲线模型进行对比分析.测试桩基的桩径为324mm，长12.81m，截面抗弯刚度为31.93MN·m2.试验土层为均质软黏土，土体重度γs＝18kN·m－3，土体平均不排水抗剪强度Su＝39.1 kPa，最大主应力差－半时的应变值ε50＝0.012.

采用现有的p－y曲线模型，计算得泥面下1d（d为桩径）深度处p－y曲线如图2所示.可见，同一深度处各模型计算得到的p－y曲线有所区别，但基本上都分为初始段和极限抗力段.不同模型p－y曲线的初始段斜率和极限抗力的大小都不尽相同.这是因为，上述p－y曲线模型基本都是来源于实测，由于土体条件、桩基结构和施工方法以及荷载类型的差异，p－y曲线的形式和计算公式各不相同.

图2 泥面下1d深度处各模型的p－y曲线Fig.2 p－ycurves of models below the ground for 1d

采用各p－y曲线模型分别计算桩顶荷载为105kN时桩的变形和内力，并与实测值相比较，见图3和图4.可见，不同p－y曲线模型计算结果差别较大，桩顶位移计算值从30mm到66mm不等，实测桩顶位移为39mm.而桩身最大弯矩计算值从125kN·m到165kN·m不等，实测最大弯矩为148kN·m.各种模型计算结果各不相同，Matlock软黏土p－y曲线与实测结果最为接近，这是因为该p－y曲线是在同一试验得到，可见实测的p－y曲线在预测同一试验桩基的变形和内力时，可以得到较准确的结果，而对于其他场地和试桩的预测，往往与实际值有差距.

图3 不同p－y曲线模型计算桩身位移Fig.3 Pile displacement of different p－ycurves

2 理想弹塑性方法

2.1 理想弹塑性模型及其可行性

如前所述，实测黏土静载p－y曲线模型基本上都可以分为初始段和极限抗力段.Matlock认为在土体进入塑性之前，p－y曲线的初始段呈1／3次方的幂指数曲线形式，而一些学者也采用了其他的函数形式，例如1／4次方的幂指数或者折线等等，这些曲线都是根据不同的试验拟合的，并且存在着不确定性，因此，土体进入塑性之前的p－y曲线形式难有定论.

朱碧堂采用理想弹塑性p－y曲线模型对大量的水平受荷桩实例进行分析，并认为通过选用恰当的模型参数，理想弹塑性模型可得到符合实际的计算结果［9］.因此，本文采用理想弹塑性曲线，见式（1）.假定土体处于弹性阶段时，桩周土反力与桩基位移成正比，且比值为常数；土体进入塑性以后，土体抗力达到极限值，不再随位移变化.p－y曲线见图5.

式中：yu为单位长度土体临界位移，yu＝pu／k.

2.2 参数取值

初始地基反力系数k反映了土体处于弹性阶段的性状，目前大都采用弹性理论分析.Biot和Vesic分别在三维弹性半空间上对无限梁在集中荷载和集中弯矩作用下解答的基础上，推导了水平地基反力系数k和土体弹性模量Es之间的关系［10－11］.朱碧堂通过比较弹性地基梁与弹性有限元分析的结果，得到土体水平抗力系数k的理论解答［9］.上述理论解答都认为弹性模量k与桩径无关，而与土体的弹性模量Es或者剪切模量G有关，并且需要引入一定的系数.而在实际工程中，上述土体参数难以得到，使得k的取值受限.

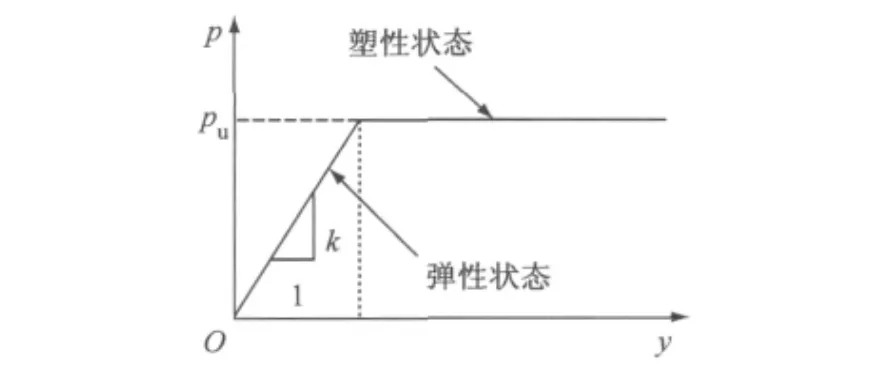
图5 理想弹塑性p－y模型Fig.5 Ideal elastic－plastic p－y model

目前国内的规范大都采用m法计算水平受荷桩，即假定桩周土体处于弹性状态，且地基反力系数随深度线性增加，深度为x的土体初始地基反力系数k可用下式表示：

式中：m为桩侧土水平抗力系数的比例系数，dp为有效桩径.

m值宜通过单桩水平静载试验确定，取10mm处的位移计算，认为此时桩周土体处于弹性阶段.当无静载试验资料时，按规范经验取值.经过多年的理论和工程实践，m值的取法积累了丰富的经验，因此可以采用m法来确定初始段土体侧压力系数k.

对于土体极限抗力pu的取值，现有的计算方法较多，有的采用经验公式，有的根据桩周土体破坏模型得到的理论公式，并根据实测进行修正.然而由于浅层土体极限抗力受到多种因素的影响，例如分层土体、表层裂隙硬黏土、地下水、施工扰动、循环荷载作用下土体抗力退化等，因此很难给出准确的理论计算公式.故采用一种可以通过参数选取拟合现有极限抗力分布的统一极限抗力.黏土的统一极限抗力［9］表达式如下：

式中：Ng为极限抗力系数；α0为反映地面土体抗力的常数或等效土体深度；n为α0与x之和的指数，极限抗力的形状参数.

通过选取合适的参数值，统一极限抗力表达式就可以包含或者近似拟合现有的极限抗力分布.对于极限抗力公式中的三个参数：Ng，n和α0，应采用现场试验得到；在没有试验的情况下，可参考下述区间的取值：Ng＝0.7～3.2.α0＝0.05～0.20m，考虑施工扰动、表层裂隙黏土以及自由水的冲刷效应等，α0可以取0.n＝0.36～1.00，均质土体，n＝0.7；上软下硬土层，n取较大值；上硬下软土层，n取较小值.

2.3 理想弹塑性方法与Matlock方法比较

影响p－y曲线的一个重要因素是土体进入塑性时水平位移界限值的确定.在Matlock软黏土p－y曲线模型中，土体水平位移临界值通过下式确定：

式中：y50为桩周土抗力达到极限土抗力一半时，相应桩的侧向水平变形；A为与桩径有关的系数，Matlock建议取2.5.

Matlock软黏土p－y曲线的现场试验中试桩直径为324mm，而实际工程中的桩基直径往往大于该值.而对于大尺寸桩，根据Matlock方法预测的桩基变形比实测值大，出现这种情况与y50的取法有关［12］.按照Matlock方法计算得到的泥面位移和桩身最大弯矩与实际值之间关系，如表1和2所示.可见，桩径越大，计算泥面位移与实测值的偏差越大，而计算桩身最大弯矩与实测值比较接近，但大多数算例也比实测值偏大.

理想弹塑性方法以极限抗力作为进入塑性的标志，在弹性阶段，水平地基反力系数k与桩径成正比；而在塑性阶段，极限抗力pu与桩径的关系受到参数n的控制，它可以根据实验得到，也可以根据经验取值.采用理想弹塑性方法计算不同直径桩基实例，得到的泥面位移和桩身最大弯矩与实际值之间关系，如表1、2所示.可见对于不同直径的桩基，计算泥面位移值均与实测位移比较接近，且计算桩身最大弯矩比Matlock方法更加接近实测值.表明Matlock软土p－y曲线对大直径桩的计算有所偏差，而理想弹塑性方法对于大直径和小直径桩的计算结果都比较接近实测值.

3 有效性验证

3.1 算例1

以Matlock软黏土中钢管桩的水平静力试验为例，桩土条件见1.2节.根据土层和桩型条件取m＝5MN·m－4，Ng＝2，n＝0.7，α0＝0.2，分别采用Matlock软黏土p－y曲线和理想弹塑性方法计算桩基性状.计算得到的桩身最大弯矩与桩顶荷载之间的关系及与实测值的对比见图6.桩顶荷载分别为33kN，69kN和105kN时桩身弯矩和位移分布见图7和图8.可以看出，该算例中理想弹塑性方法预测结果与Matlock软黏土p－y曲线的预测结果一致，与实测桩基性状相符.

表1 计算泥面位移与实测值之比与桩径的关系Tab.1 Ratio of the computed and measured groundline deflection to pile diameter

表2 计算桩身最大弯矩与桩径的关系Tab.2 Comparison of the computed maximum pile moment to pile diameter

图6 桩身最大弯矩与荷载关系图Fig.6 Curves of maximum pile moment and load

3.2 算例2

南京水利科学研究院和河海大学于1982年在镇江进行了水平向荷载桩短期静载试验［7］，测试桩基的桩径为1200mm，壁厚19mm，抗弯刚度为2877MN·m2，入土深度45m，泥面以上至加载点的自由高度为7.9m.试验土层为砂质软黏土，土体重度γs＝18kN·m－3，平均不排水抗剪强度Su＝15 kPa，ε50＝0.02.根据上述条件取m＝6MN·m－4，Ng＝2.6，n＝0.7，α0＝0.2，采用统一极限抗力方法计算桩基性状.

分别采用Matlock方法和理想弹塑性方法进行计算，得到的桩身最大弯矩和桩顶位移与桩顶荷载关系曲线见图9和图10，可以看出桩身最大弯矩基本与实测曲线一致，但是Matlock p－y曲线的桩顶位移的计算结果明显偏大，这主要是由于本算例桩径较大，因此根据公式（4）计算的土体界限位移偏大，达到塑性的桩身位移较大，土体反力系数较小，导致计算结果偏大.

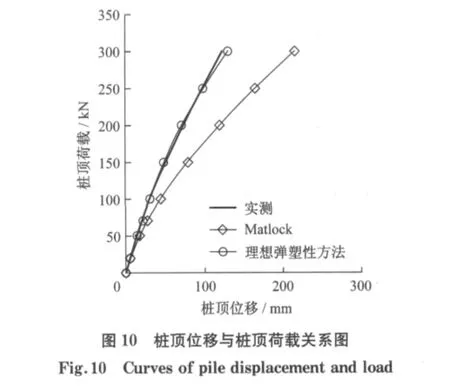
图11和12分别给出了桩顶荷载为100kN，200kN和300kN时，两种方法计算的桩身弯矩和位移分布图及其与实测值对比情况.可以看出，Matlock计算方法对于大直径桩计算的桩身位移偏大，桩身弯矩的反弯点明显偏低，并且随着桩顶荷载的增加，这种现象更加明显.而理想弹塑性方法计算结果与实测数据吻合较好，这与2.2节的计算结果也是一致的.

4 结语

目前，计算黏土中水平受荷桩的p－y曲线模型很多，但大都是基于某个现场试验或者室内试验得到的，普适性较差.为了改善对实测p－y曲线方法的依赖，本文主要做了以下几个方面的工作：

（1）总结和分析目前实测p－y曲线模型，并指出实测的p－y曲线普适性较差.

（2）论证采用理想弹塑性模型的可行性，建议了理想弹塑性模型的参数取值，并验证了该模型和参数可用于不同直径桩基.

（3）通过两个算例验证，证明理想弹塑性的有效性.

理想弹塑性方法的优点在于p－y曲线形式简单，意义明确，并能准确地预测黏土中水平受荷桩基的变形和内力分布.该方法既可以应用于小直径桩基，也可应用于大直径桩基，普适性较好，有利于工程应用.

［1］McClelland B，Focht J A.Soil modulus for laterally loaded piles［J］.Journal of the Soil Mechanics and Foundations Division，ASCE，1958，82（4）：1049.

［2］Matlock H.Correlations for design of laterally loaded piles in soft clay ［C］／／The 2nd Annual Offshore Technology Conference，Houston.Houston：［s.n.］，1970，1：577－594.

［3］Reese L C，Cox W R，Koop F D.Field testing and analysis of laterally loaded piles in Stiff Clay［C］／／The 7th Annual Offshore Technology Conference，Houston.Houston：［s.n.］，1975，2：671－690.

［4］Reese L C，Welch R C.Laterally loading of deep foundations in stiff clay［J］.Journal of the Geotechnical and Engineering Division，1975，101（7）：633.

［5］Sullivan W R，Reese L C，Fenske C W.Unified method for analysis of laterally loaded piles in clay［C］／／Institution of Civil Engineers，Numerical in Offshore Piling.London：IEC，1980：135－146.

［6］Dunnavant T W，O’Neill M W.Experimental p－y model for submerged stiff clay［J］.Journal of Geotechnical Engineering，1989，115（1）：95.

［7］王惠初，鲁子爱.p－y曲线法在镇江大港横向受载桩基中的应用［J］.华东水利学院学报，1986，14（1）：124.WANG Huichu，LU Ziai.Application of p－y curve method in laterally loaded piles at Port Dagong［J］.Journal of East China Technical University of Water Resources，1986，14（1）：124.

［8］章连洋，陈竹昌.计算黏土p－y曲线的方法［J］.港口工程，1992，10（4）：50.ZHANG Lianyang，CHEN Zhuchang.A new p－y curve construction method in cohesive soils ［J］. The Ocean Engineering，1992，10（4）：50.

［9］朱碧堂.土体的极限抗力与侧向受荷桩性状［D］.上海：同济大学土木工程学院，2005.ZHU Bitang.Limiting force profile and response of laterally loaded piles［D］.Shanghai：Tongji University.College of Civil Engineering，2005.

［10］Biot M A.Bending of an infinite beam on an elastic foundation［J］.Journal of Applied Mechanics，1937，4（3）：A1.

［11］Vesic A B.Beams on elastic subgrade and the Winkler′s hypothesis［C］／／The 5th International Conference on Soil Mechanics and Foundation Engineering.Paris：dunod Editeur，1961：845－851.

［12］Stevens J B，Audibert J M E.Re－examination of p－y curve formulations［C］／／The 11th Annual Offshore Technology Conference，Houston.Houston：［s.n.］，1979：397－402.