大口径薄壁海底管道局部屈曲设计技术研究★
张 先 锋
(中石化石油工程设计有限公司,山东 东营 257026)
1 概述
近年,随着海洋油气储运业的发展,海底管道的建设活动越来越多,建成了一些大口径的海底管道[1]。大口径海底管道的焊接、施工方法等方面都有较大的进步和发展[2,3]。但是在管道的强度设计分析方面,在现行的海底管道设计标准中[4],对径厚比大于45的海底管道都没有规定明确的设计方法。对大口径海底管道而言,若要在设计过程中控制管道的径厚比满足现有标准的适用条件,需要选择较大的钢管壁厚,这将会增加钢材用量和海上焊接时间,增加工程投资。本研究通过对大口径薄壁海底管道在弯矩作用下的局部屈曲分析,引入了弯曲抗力系数,建立了弯矩抗力系数与管道径厚比的关系。
2 大口径薄壁海底管道局部屈曲模拟
2.1 理论弯矩抗力
海底管道的局部屈曲的理论弯矩抗力为:
Mp=fy×(D-t)2×t。
其中,Mp为塑性弯矩抗力,N;Sp为塑性轴力抗力,N;D为管道外径,N;t为管道壁厚,N;fy为材料屈服强度,Pa。
将实际弯矩抗力与理论弯矩抗力的比值定义弯矩抗力系数γMP,即:
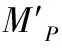
则内部超压海底管道局部屈曲校核公式变为:
其中,γm为材料抗力因子,无量纲;γSC为安全等级抗力因子,无量纲;Msd为设计弯矩,N·m;Ssd为设计有效轴力,N;pi为管道内压,Pa;pe为管道外压,Pa;MP为塑性弯矩抗力,N·m;SP为塑性轴力抗力,N;pb为承压抗力,Pa;t2为管道壁厚,m;αc为考虑应变硬化的流动应力参数;αmd为考虑点荷载影响的塑性弯矩抗力折减系数,无量纲;αp为压力因子,无量纲。
2.2 钢管本构关系
管道局部屈曲分析中,考虑材料的非线性影响,其应力应变本构关系遵循Ramberg-Osgood模型,即:
其中,ε为总应变,无量纲;σ为应力,Pa;E为弹性模量,Pa;αr为Ramberg-Osgood系数,无量纲;σo为名义屈服应力,Pa;N为Ramberg-Osgood指数,即:
其中,εo为屈服应变,无量纲;σu为最小抗拉强度,Pa;εu为极限强度应变,无量纲。
2.3 有限元分析
采用有限元法分别研究五种管径φ1 016,φ1 118,φ1 219,φ1 321,φ1 422管道在不同壁厚条件下的局部屈曲失效承载力。管径与壁厚组合情况见表1。
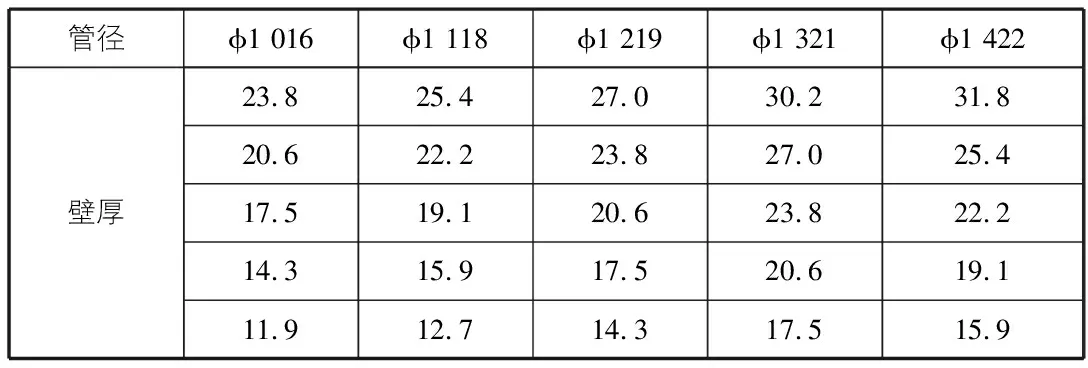
表1 典型截面组合表 mm
管道有限元模型如图1所示。

根据对海底管道在弯矩作用下的局部屈曲模拟分析,得出φ1 016,φ1 118,φ1 219,φ1 321,φ1 422管道的实际弯矩抗力见表2~表6。
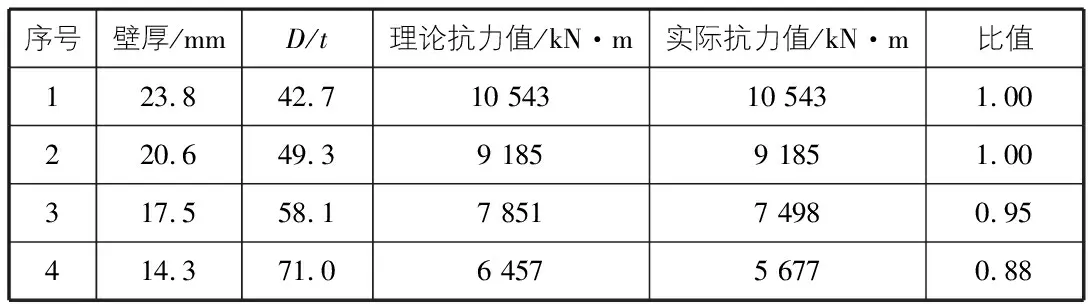
表2 φ1 016管道弯矩抗力结果
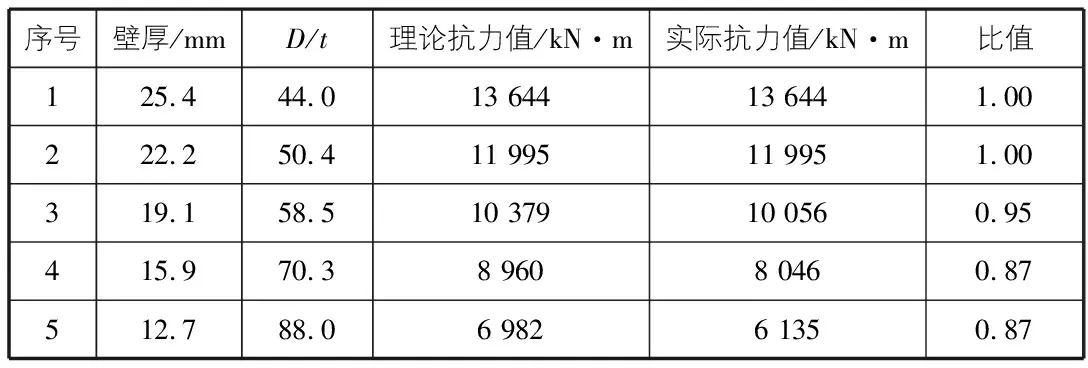
表3 φ1 118管道弯矩抗力结果

表4 φ1 219管道弯矩抗力结果

表5 φ1 321管道弯矩抗力结果
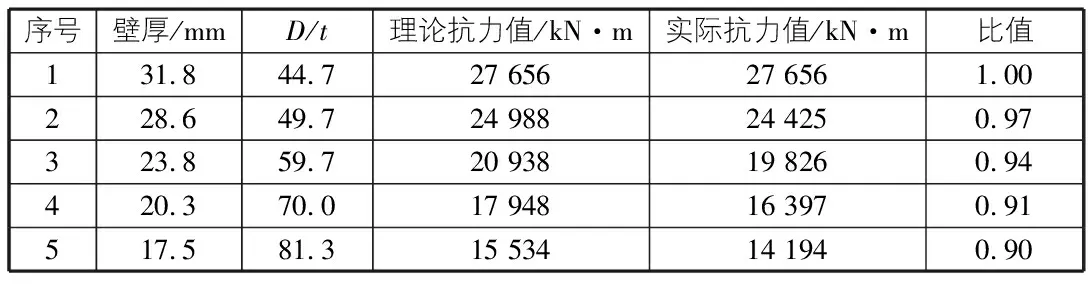
表6 φ1 422管道弯矩抗力结果
根据上述不同管径、不同径厚比条件下管道弯矩抗力系数可知,当径厚比大于45时,管道的局部屈曲弯矩抗力会随着管道径厚比的增大而降低,弯矩抗力系数与管道径厚比的关系如图2所示。
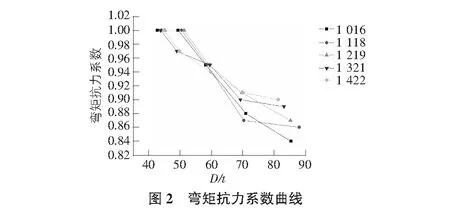
基于设计包络线方法,弯矩抗力系数可按下式取值:
3 结论与建议
本研究通过对大口径薄壁海底管道在弯矩作用下的局部屈曲分析,引入了弯曲抗力系数,建立了弯矩抗力系数与管道径厚比的关系。研究结果表明,大口径薄壁海底管道的弯曲抗力系数随径厚比的增大而减小。

