生命线工程网络抗震优化算法研究

刘 威，李 杰

（1.同济大学 土木工程防灾国家重点试验室，上海 200092；2.同济大学 建筑工程系，上海 200092）

生命线工程系统是维系现代城市与区域经济功能的基础性工程设施系统［1］.大多数生命线系统是以网络的形式分布在城市或较大的区域范围内，如城市的供水、供燃气管网，区域的电力网络等.对生命线工程系统而言，仅仅实现各个单体的抗震性能分析以及系统的整体性能评价远远不够，更重要的是利用这些分析工具进行网络抗震性能的优化设计，以最低造价保证系统具有足够的抗震性能［1］.

管网系统的抗震可靠性优化可以从提高系统单元的抗震可靠度和改进网络的拓扑结构两条路径来进行.研究表明［1］，综合考虑工程实际中的各种因素，改进网络拓扑结构，要明显优于仅仅提高单元的抗震可靠度.在管网抗震拓扑优化方面，文献［2］利用遗传算法进行了基于抗震功能可靠性的供水系统拓扑优化研究.文献［3－4］则采用遗传算法和模拟退火算法，初步实现了基于连通可靠度分析的生命线管网拓扑优化.已有研究工作表明，遗传算法和模拟退火算法各有特点，其优劣尚没有比较研究.

本文首先介绍了基于生命线管网抗震连通可靠度的工程网络系统的抗震拓扑优化模型，然后分别介绍利用遗传算法、模拟退火算法和遗传－模拟退火混合算法进行生命线网络系统的抗震拓扑优化方法.同时，利用两个算例对比分析上述三种算法的计算效率和计算结果.

1 管网优化模型的建立

工程实际中，在保证安全合理的情况下，经济性是优化改造和优化设计的主要目标.本管网系统优化以网络的拓扑结构为优化对象、抗震可靠度为优化约束条件、管网建设造价为优化目标来进行.

管网系统的造价一般可以写为

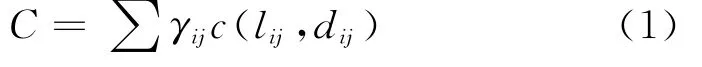
式中：lij，dij分别为i，j节点之间的管线长度和直径，m；γij为连通系数，铺设该管线取1，不铺设则取0；c（lij，dij）表示管线的造价，通常用下列函数估算：

式中：a1，a2和a3都是常数，可以根据实际工程的造价采用回归方法得到.对于供燃气网络，则可以分别取为－144.3609，4313.3000和1.0000［5］.

以供燃气管网的造价为优化目标，可以建立如下的优化模型：

式中：Pmin为管网节点的抗震可靠度最小值，可采用最小路递推分解算法［6］获得；P0为管网节点的抗震可靠度约束.

2 单元重要度分析

显然，系统中每个单元对系统可靠度的贡献是不同的，有些单元的贡献比较大，而另外一些单元则比较小.对网络系统单元进行重要度分析，能够为确定网络系统的优化方向提供信息.

一般情况下，网络系统的单元重要度依赖于单元可靠度和系统可靠度.曹晋华等［7］给出了网络系统中单元r的概率重要度定义

式中：PS，Pf分别为系统的可靠度和失效概率；pr，qr分别是网络系统中r单元的可靠概率和失效概率.可以看出，r的概率重要度是网络系统S的可靠度对r可靠概率的变化率.因此越大，即Iprob，r越大，r对系统可靠度的影响也越大，也就越重要.

由最小路递推分解算法［6］，可得单元r对节点i的概率重要度计算公式为

式中：Lm为求节点i连通可靠度时系统的一条不交最小路；R为所有的不交最小路数目.而P（Lm）对r可靠度的偏导数为

然而，单元概率重要度只反映单元的可靠度变化对系统可靠度的影响，无法反映单元的投资效率.考虑造价因素，可以引入投资重要度概念.任意单元r对节点i的投资重要度定义为

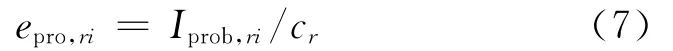
式中：cr为网络系统中r的造价，由式（2）计算得到.

可见，单元投资重要度的实质是单位造价的单元概率重要度.单元的投资重要度越高，说明通过改造此单元，可以较少的费用获取系统可靠性较大的提高.所以，单元的投资重要度是一个重要的设计参数，能够指导系统可靠度优化设计.

3 遗传算法

遗传算法是由美国科学家Holland［8］借鉴生物进化原则提出的一种自适应并行全局优化概率搜索算法，近年来发展迅速，在各领域广泛应用［9－10］.

下面结合管网系统的拓扑结构优化问题来介绍基本遗传算法的具体运算步骤与原理.

3.1 编码

采用0－1编码，当基因值为0时，表示该基因对应的管线不铺设；当基因值为1时，表示铺设该基因对应的管线.所有优化参数对应的基因按照指定的次序排列起来，就构成一条染色体.一个染色体对应管网的一种拓扑结构方案，多条染色体构成遗传算法的一个种群.

3.2 生成初始种群

采用随机策略来生成一组个体.但必须注意，随机生成的管网拓扑结构可能是工程中无意义的解.例如，非连通图对应的管网结构在工程实践中无意义.所以，在随机生成个体后，首先要判断管网拓扑结构的合理性.对于不合理个体，简单地修补；修补后的个体仍不合理，则抛弃之，重新生成新个体.

3.3 个体评价

因管网拓扑优化目标是获得满足抗震可靠度要求的最低造价管网，而遗传算法中一般定义适应度高的解为较优解，故定义染色体的适应度函数为

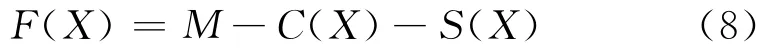
式中：M为预先指定的一个较大数值；C（X）为个体对应管网的造价；S（X）为惩罚函数，用下式计算：

式中：Cmax，Cmin为当前群体中个体造价的最大、最小值；Pmin，u为当前群体中第u个体中节点连通可靠度最低值；v＝1，2，…，K，K为当前群体个体数.

3.4 遗传操作

遗传操作包括选择、交叉和变异操作.选择操作采用无放回的适应度比例方法和最佳个体保存方法.即上一代最优的个体必然进入到下一代，并且上一代的每个个体遗传到下一代中只有一个.交叉操作选择一点交叉方法进行.变异操作对个体的每一个基因位，按一变异概率对其值作取反运算，从而产生一个新的个体.下面结合管网单元的投资重要度来确定管网中每个单元的变异概率.

首先，计算管网中各个单元的重要度

式中：epro，ri为网络中第r个单元对第i个节点的投资重要度，由式（7）得到；n为网络中不满足节点可靠度最低约束要求的节点数；N为网络所有节点数.

当网络中单元对应的基因为0时，则其通过变异操作变为1的变异概率由下列线性插值公式计算：

式中：Pmax，01，Pmin，01为单元从0转换为1的最大概率和最小概率，分别取0.8和0.5；Imax，Imin为当前网络中单元重要度的最大值和最小值.

当网络中单元对应的基因为1时，其通过变异操作变为0的变异概率由下列线形插值公式计算：

式中：Pmax，10，Pmin，10为单元从1转换为0的最大概率和最小概率，分别取0.4和0.1.

经过式（11）和（12）的计算，重要度大的单元从0变为1的概率高，从1变为0的概率低；而重要度小的单元则相反，从0变为1的概率低，从1变为0的概率高.显然，利用单元投资重要度可在一定程度上确定搜索方向，加快优化收敛速度.

3.5 收敛判断

遗传算法通常的停止规则有计算达到固定的最大进化代数、解群体间差异充分小等规则.笔者采用计算达到固定的最大进化代数.

4 模拟退火算法

4.1 基本原理和计算步骤

模拟退火算法的思想最早由 Metropolis［11］提出，由Kirkpatrick［12］在1983年成功地应用在组合最优化问题中.模拟退火算法是模拟物理系统退火过程的随机性迭代寻优方法，具有易实现和全局渐近收敛的特点.理论上已经证明［13］，如果计算无限次，模拟退火算法必然搜索到全局最优解.

模拟退火算法用如下准则确定的转移概率来确定是否接受从当前解u到新解v的转移：

对于管网的拓扑优化问题，模拟退火算法的具体操作步骤为：

① 随机产生一个初始解，以此作为当前最优点并计算目标函数值.

②根据初始温度及降温函数确定当前温度t，如果t低于终止温度，则结束计算，否则转③.

③ 随机变动当前最优点，产生一个新解，计算新解的目标函数，根据式（13）确定接受新解的概率.

④ 产生一个随机数，如果其小于或等于接受新解的概率，则接受新解，否则拒绝.

⑤判断当前温度下计算次数是否达到规定的次数，若是转②，否则转③.

模拟退火算法除接受优化解外，还在一个限定范围内接受恶化解.这正是该算法与其他局部搜索算法的本质区别.

4.2 有关参数和技术

（1）目标函数 管网拓扑优化的目标是获得满足节点最低可靠度约束条件下造价最低的管网.在模拟退火算法中，目标函数低的解优于目标函数高的解，故采用如下方法计算目标函数：

式中：C（u）为个体对应管网的造价；Psum，u＝（P0－Pv），当P0＞Pv时；α，β为常数，分别取10和1.

（2）温度参数的控制 温度参数是模拟退火算法中最关键的参数，主要包括起始温度t0的选取、温度的下降方法、每一温度迭代次数的确定等.

从理论上来说，起始温度应保证平稳分布中每一个状态的概率相等，也就是使

式中，Δfuv＝f（u）－f（v）.因此，t0需要取一个较大的数值，现采用的估计值为t0＝10 Cmax.

采用如下的温度更新函数来模拟降温过程：

式中，γ为降温系数，一般0＜γ＜1，本文取为0.7；k为当前进化的代数.模拟退火算法每一温度的迭代长度采用固定长度法获取.固定长度法是一个最简单的方法，在每一温度，迭代相同的步数.

（3）随机扰动模型 模拟退火算法从一初始解出发，通过降温迭代寻找最优解.在降温过程中，不断地对当前解随机扰动以产生新解.可以采用遗传算法中变异操作方法来进行.注意到模拟退火算法中只有一个解且并不一定接受劣解，故此时的Pmax，01，Pmin，01以及 Pmax，10，Pmin，10均应大于相应遗传算法的值，取值分别为0.9，0.6和0.6，0.3.

（4）算法的终止原则 采用零度法，即给定一个较小的终止温度tf，当温度tk≤tf时，算法停止.

5 遗传-模拟退火混合算法

实践表明，遗传算法容易早熟，导致无法搜索到最优解.究其原因，主要是生成新解的过程主要依靠交叉操作，而变异操作一般由于变异概率过小而作用不大，从而搜索范围过小.为了克服这个问题，考虑到模拟退化算法中的扰动操作过程类似于变异操作，同时这一过程产生的解变异性较大且会以一定概率接收，其可以增强遗传算法的搜索能力，故将模拟退火算法引入到变异操作中，可以发展出一类遗传－模拟退火混合算法［14］.

混合算法计算过程与遗传算法基本上一样，只是在变异操作时采用模拟退火操作.这里的模拟退火操作，实际上相当于模拟退火算法在同一温度下多次操作扰动产生新解→判断优劣→以一定概率接收新解的过程.这一过程中，温度由初始温度和当前进化的代数决定，即式（16）中的k为当前进化代数.因此，遗传－模拟退火混合算法的计算过程如下：

① 随机产生一个初始种群作为当种种群.

② 对当前种群分别进行选择、交叉操作，对交叉操作产生的每个管网分别进行模拟退火操作.

③将上述三个操作产生的所有管网合并起来作为当前种群.

④ 重复②和③，直到种群代数达到规定数.

6 分析实例

6.1 算例1

图1为一供燃气网络系统，源点为1，节点2～10为汇点，管线单元属性见表1，总造价为5920万元.假设各管线单元抗震可靠度都为0.9.

图1 算例1的管网Fig.1 Network of Example 1

表1 图1管网单元属性Tab.1 Pipeline characteristics of the network in Figure 1

由于该网络至少要有9条边才能形成一棵最小树，故全部可行子网为＝3473个.对上述3473个子网分析连通可靠度，发现相应节点最低可靠度约束分别为0.7，0.8和0.9的最优网络分别如图2所示［15］.分别利用三种优化算法优化管网.三种算法的参数为：①遗传算法，种群个体数为90，计算代数为50，交叉操作概率为0.8.②模拟退火算法：同一温度下迭代步数为50.③遗传－模拟退火混合算法，种群个体数为90，计算代数为50，交叉操作概率为0.8，同一温度下迭代步数为5.

为了比较计算效率，每种算法分别计算1000次，每次计算都是将算法从头开始重新计算.各算法得到图2的最优结果的次数如表2所示.

图2 算例1的可靠度约束分别为0.7，0.8，0.9时的最优网络Fig.2 The optimal network when p0is 0.7，0.8，0.9for example 1

表2 算例1的三种算法计算效率对比Tab.2 Efficiency comparison of three algorithm for example 1 次

从表2可以看出，三种算法中，遗传－模拟退火混合算法的计算效率相当好，几乎每次都可以搜索到最优结果；而模拟退火则性能比较差，大约只有20%～30%的次数搜索到了最优解；遗传算法的搜索能力则介于两者之间.

6.2 算例2

图3中的供燃气网络系统比算例1复杂.其源点为1，节点2～16为汇点，管线单元属性和抗震可靠度见表3，管网总造价为3048万元.由于该网络至少要有15条边才能形成一棵最小树，故全部可行子网中＝2579130≈260万个.对上述260万个子网分析连通可靠度，获相应节点最低可靠度约束P0分别为0.7，0.8和0.9的最优网络（见图4）.

图3 算例2的管网Fig.3 Network of Example 2

分别采用三种算法来优化，计算参数同算例1.由于这个算例比算例1复杂，从计算时间上考虑，每种算法只分别计算100次.各算法得到图4的最优结果的次数如表4所示.

从表4可以看出，与算例1一样，遗传－模拟退火混合算法的计算效率最好，大约有70%的次数可以搜索到最优结果；而模拟退火则性能比较差，只有不到20%左右；遗传算法则介于两者之间.

表3 图3的管网单元属性Tab.3 Pipeline characteristics of the network in Figure 3

从上面两个算例可以看出，对于本文的管网抗震拓扑优化问题，混合算法性能最好，遗传算法次之，而模拟退火算法较差.两种算法较好的原因在于它们均为并行算法，每个种群中基因数较多，因此在产生新的种群时可利用的信息较多.模拟退火算法实质是一种串行算法，在产生新解时只有一个解的信息可利用.另外，混合算法用模拟退火操作代替遗传算法中的变异操作，有效地增加了算法的搜索空间，改善了遗传算法中变异操作产生新解能力较差的问题，使得性能有了较大地提高.

表4 算例2的三种算法计算效率对比Tab.4 Efficiency comparison of three algorithms for example 2 次

7 结论

对10节点14条边的燃气管网优化分析表明，遗传－模拟退火混合算法的性能最好，几乎每次都可搜索到最优结果；模拟退火则性能较差，大约只有20%～30%的次数搜索到最优解；遗传算法的搜索能力则介于两种算法之间，约有58%～80%的次数搜索到了最优解.对16个节点24条边的网络分析可以给出类似的结论：遗传－模拟退火混合算法的计算效率最好，大约有70%的次数搜索到最优结果；而模拟退火则性能比较差，只有不到20%左右的次数搜索到了最优解；遗传算法的搜索能力则介于两种算法之间，约有20%～40%的次数搜索到最优解.

［1］李杰.生命线工程抗震：基础理论与应用［M］.北京：科学出版社，2005.LI Jie.Lifeline earthquake engineering：basic method and application［M］.Beijing：Science Press，2005.

［2］陈玲俐.城市供水管网系统抗震可靠性分析与优化［D］.上海：同济大学土木工程学院，2002.CHEN Lingli.Seismic reliability analysis and optimization of urban water distribution networks［D］.Shanghai：Tongji University.College of Civil Engineering，2002.

［3］包元峰，李杰.基于遗传算法的生命线工程网络抗震优化设计［J］.防灾减灾工程学报，2006，26（1）：21.BAO Yuanfeng，LI Jie.Seismic reliability optimization of lifeline system networks with genetic algorithms［J］.Journal of Disaster Prevention and Mitigation Engineering，2006，26（1）：21.

［4］包元锋.生命线工程网络系统抗震可靠性分析与优化［D］.上海：同济大学土木工程学院，2004.BAO Yuanfeng.Seismic reliability analysis and optimization of lifeline systems networks［D］.Shanghai：Tongji University.College of Civil Engineering，2004.

［5］王烜.城市燃气管线网络系统优化设计研究［D］.哈尔滨：哈尔滨工业大学市政环境工程学院，2005.WANG Xuan.Optimization design research on urban gas network system［D］.Harbin：Harbin Institute of Technology.School of Municipal and Environmental Engineering，2005.

［6］LIU Wei，LI Jie.An improved recursive decomposition algorithm for reliability evaluation of lifeline networks［J］.Earthquake Engineering and Engineering Vibration，2009，8（3）：409.

［7］曹晋华，程侃.可靠性数学引论［M］.北京：科学出版社.1986.CAO Jinhua，CHENG Kan.Reliability mathematics［M］.Beijing：Science Press，1986.

［8］Holland J H.Adaptation in natural and artificial systems［M］.Cambridge：MIT Press，1975.

［9］Gazen C，Ersoy C.Genetic algorithms for designing multihop lightwave network topologies［J］.Artifical in Intelligence Engineering，1999，13：211.

［10］Saha D，Purkayastha M D，Mukherjee A.An approach to wide area WDM optical network design using genetic algorithm［J］.Computer Communications，1999，22：156.

［11］Metropolis N，Rosenbluth A，Rosenbluth M，et al.Equation of state calculations by fast computing machines［J］.Journal of Chemical Physics，1953，21：1087.

［12］Kirkpatrick S，Gelatt C D Jr，Vecchi M P.Optimization by simulated annealing［J］.Science，1983，220：671.

［13］邢文训，谢金星.现代优化计算方法［M］.北京：清华大学出版社，1999.XING Wenxun，XIE Jinxing.Modern optimization algorithm［M］.Beijing：Tsinghua University Press，1999.

［14］Jeong I，Lee J.Adaptive simulated annealing genetic algorithm for system identification［J］.Engineering Applications of Artificial Intelligence，1996，9（5）：523.

［15］刘小坛，刘威，李杰.生命线网络系统抗震拓扑优化的Benchmark模型［J］.防灾减灾工程学报，2007，27（3）：258.LIU Xiaotan，LIU Wei，LI Jie.Benchmark models for seismic topological optimization problem of lifeline systems［J］.Journal of Disaster Prevention and Mitigation Engineering，2007，27（3）：258.