Focal Shift and Focal Switch of Elegant Cosh-G aussian Beams
WEN Wei, SHI Zhen-gang, DENG Xiao-peng
(1.Department of Physics and Information Engineering; 2.Research Institute of Information Science,Huaihua University,Huaihua,Hunan 418008)
Focal Shift and Focal Switch of Elegant Cosh-G aussian Beams
WEN Wei1,2, SHI Zhen-gang1,2, DENG Xiao-peng1,2
(1.Department of Physics and Information Engineering; 2.Research Institute of Information Science,Huaihua University,Huaihua,Hunan 418008)
Abstract:Strarting from the collins diffraction integral,the formula predominating the distribution of axial intensity of elegant cosh-Gaussian beams(EchG)through thin lens without aperture and the third-order equation governing the position of axial maximum intensity is derived and the analytical condition of focal switch of EchG beams is obtained.A large number of numerical calculation results are presentedon this basis.It is shown that relative incidence distance and beams parameters influence focal switch besides the Frensel numbers.These results are helpful to understanding the focusing properties of EchG beams.
Key words:focal shift; focal switch; elegant cosh-Gaussian beams; the lens without aperture
CLC number:O436Document:AArticle ID:1671-9743(2010)05-0043-05
1 Introduction
It is well known that,when a beam is diffracted by a circular aperture,the position of axial intensity maximum does not located at the geometric focus,but it is slightly displaced towards the aperture plane[1,2].This effect is called the focal shift.Recently,Martinez,Climent and Li found that,in special optical systems such as system with a certain kind of diffracting screen and dualfocus systems with Fresnel zone plate,the focal shift can develop to a rapid focal switch,namely the point of absolute maximum intensity moves suddenlyfrom a point to another[3,4].These phenomena have become a subject of laser research because of the requirement to determine the real focal plane accurately in practical applications[5-7].
The Hermite-sinusoidal-Gaussian beams are one of the solutions of the paraxial wave equation in the rectangular coordinate system shown by Casperson and T ovar in recent years[8].The cosh-Gaussian beams are regarded as the special cases of Hermite-sinusoidal-Gaussian beams,are of practical interest because of their efficient in extracting energy from conventional laser amplifiers,and they have some important applications because their profiles can resemble closely the flat -top field distribution by choosing suitable beam parameters of cosh parts[9-11].On the other hand,elegant beams, introduced by Siegman,differ from standard beams because the former contain polynomials with a complex argument, whereas in the latter the argument is real.The significance of elegant beams are that they are closely related to multipole fields,they describe propagation through a complex parabolic medium,and they arise in the higher-order connection terms of perturbation expansions of the solutions of the wave equation whose leading term is the fundamental Gaussian beam function[12-14].For cosh-Gaussian beams,they are the solutions of the Helmholtz equation when the beam parameters of cosh parts are complex and which can get better flat-top field distribution.
This paper is organized as follows.In Section 2,a closed-form propagation equation of EChG beams is derived.In section 3,the numerical results are presented and the dependence of the focal shift and focal switch on the parameters are discussed in detail.Finally,Section 4 summarizes the main results obtained in this paper.
2 Theoretical modal
As shown in Fig.1,a single thin lensof focal length f located at the propagation path is considered,RP1indicates theaperture plane and RP2means the out-put plane.Considering a EchG beam,in the cartesian coordinate system,whose field distribution at thez=0 plane reads
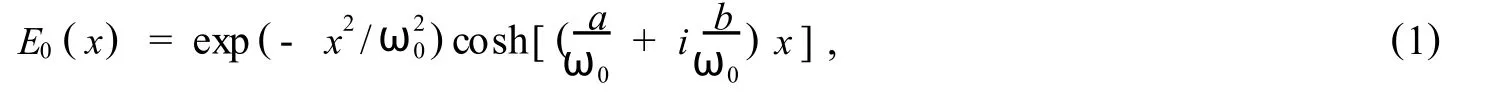
Whereω0is the waist of the Gaussian amplitude distribution,and a and b are parameters related to hyperbolic-cosine.The propagation of the EchG beam through an unapertured converging thin lens can be described by collins formula[15],So the field distribution at the outplane RP2is given by
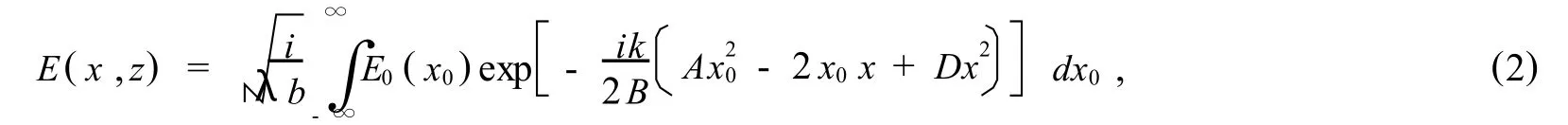
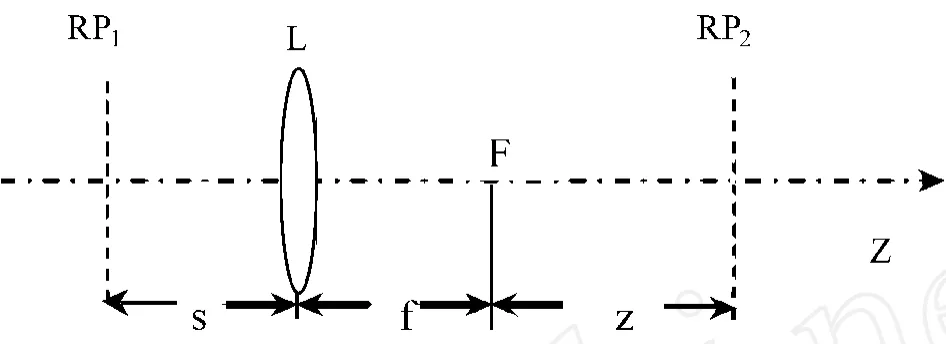
Fig.1 A lens Optical system without aperture
wherekis the wave number related to the wavelengthλbyk=2π/λ;A,BandDare elements of the transfer matrix lens system which reads as

By inserting Eq.(3)into Eq.(2),we get the irradiance intensity of the focused EchGis give by I= E*E*
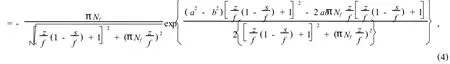

On substituting from Eq.(4)into Eq.(5)leads to the third-order algebraic equation governingzmax:
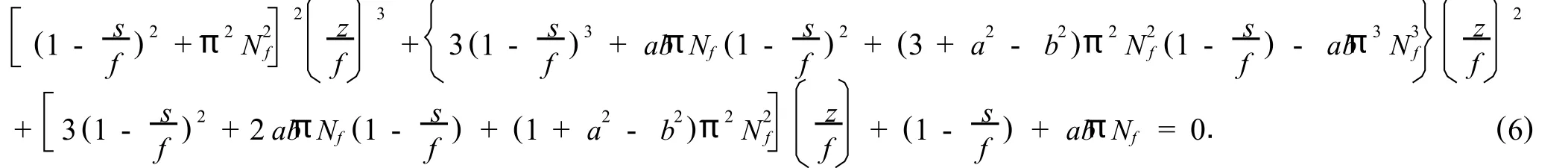
Eqs.(4)and(6)are basic analytical results obtained in this paper. The relative focal shift is defined as

where R is the position of the geometrical focal point of EchG beams focused by the lens,and is given by

From Eqs.(6)and(7),it can be seen that the relative focal shift non-vanishing in general.In other words,the focal shift is commonly occurring,this is the marked differences between physical optics and geometric optics.
There are two maximum intensity on the axial determined by condition

Substituting Eq.(6)into Eq.(9),and after some algebraic manipulations the condition can be expressed as

When Eq.(10)is getting satisfaction,there exist three extreme value on the propagation axis,including two maximum value and one mimimum value.The irradiance intensity have two maximum value and competition each other,it can on demand lover turn up the focal switch phenomenon.From Eq.(10)one can arrival at a conclusion that there can take place focal switch even if the Fresnel numberNfis large or relative separations/f≠1.
If we makes/f=1,one can get

Eq.(11)is simplified form of Eq.(10)and the necessary condition for arise focal switch of EchGbeams when s/f =1.In fact,there are many laser beams can take place this phenomenon if s/f=1[14,15].It can be seen that Eq.(11)are not satisfied ifa=b=0,that is to say,there isn't focal switch for fundamental mode Gaussian beams.Whena=0 but b≠0,EchG beams degenerate into cosine-Gaussian beams,one can deduced that there existential focal switch phenomenon if(1-b2)<0(b>1),namely the resultsof literature[18].Moreover,ifa≠0andb=0,Eq.(11)can not be met,so we conclude that there can not occurrence focal switch phenomenon for cosh-Gaussian beams[19].
3 Numerical results and analysis
A large number of numerical calculations were performed by using the above equations to illustrate the focusing properties and focal switch effect of EchG beams passing through a system with the aperture and lens separated.
Fig.2 represents the axial intensity of the focused EchG beams with a certain smaller value ofasay 0.2 in different relative incident distancess/f,respectively.The other calculation parameters areb=1.5,Nf=2.0.From Fig.2,it can be seen that the peak of the axial intensity is shifted slightly toward the lens.Fors/f=0.01,there exists only one maximum of axial irradiance.However,whens/fincreases gradually,the second lobe of the axial irradiance appears and its height increases with increasing of the relative incident distance.In particularly,the heights of the central and second lobes are equal whens/f=1.Therefore,the critical point arrives at which the focal switch,namely,a permutation of the focal point,takes place whens/fgoes beyond this limit.With a further increases ofs/f,the height of the second lobe increases,while the central lobe decreases,so that the height of second lobe is larger than that of the central lobe.The focal switch phenomenon can be explained for the competition of two irradiance maximum.
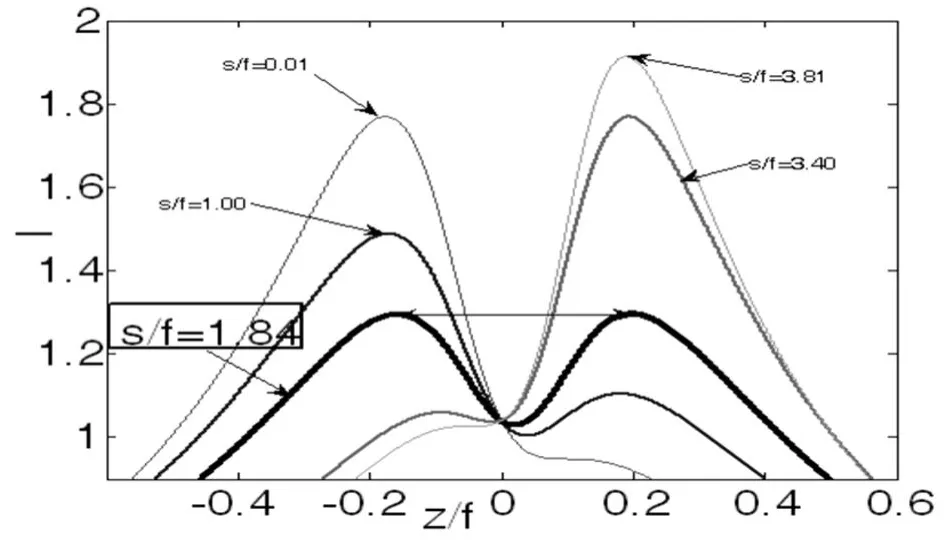
Fig.2 Axial irradiance distributionIfor different values ofs/f.a=0.2,b=1.5,NF=2.0
On the other hand,the axial intensities of focused EchG beams for different beam parametersband differentz/fare depicted in Fig.3(Nf=2.0,a=0.5,s/f=1.5).As can be seen,for b less than the critical value,there exists only one axial intensity maximum,and the positionzmaxof the axial intensity maximum coincides with the geometrical focal point of the lens.It means that the focal shift andfocal switch phenomena will disappear beyond this value.However,for b greater than the critical value,the result shows that there exist two axial intensity maxima with equal value,which are located at equal distance on the two sidesof the geometrical focus.It means tiat the focal shift andfocal switch phenomena come about.
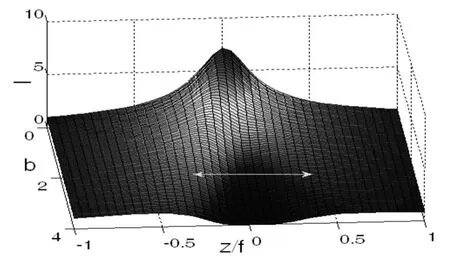
Fig.3 Axial irradiance distribution Ifor different values ofz/fand b.Nf=2.0,a=0.5,b=1.5.
The corresponding relative focal shiftΔzfversus s/f is shown in Fig.4.As can been seen,Δzfchanges with s/f.At the turning point s/f,there exists a critical valueacin Fig.4(a)andbcin Fig.4(b),respectively.And the focal switch vanish whena> acandb<bc.On the contrary,whena<acandb>bc,there is a rapid transition at the turning point in Fig.4(a)and Fig.4(b),respectively,andΔzfchanges form the negative sign to the positive one as the s/f increases,it means that the focal switch takes place.The negativeΔzfimplies that the real plane is shifted toward the lens relative to the geometrical focal plane.

Fig.4 Relative focal shiftΔzfversus relative separations/f.(a)NF=2.0,b=1.5(b)NF=2.0,a=0.2
Furthermore,the axial intensity maximumImaxof the EchG beams passing through a single thin lens versus relative separation s/f for different value ofNfare given.From Fig.5,it can thatImaxreaches its minimum at the turning point with different s/f.
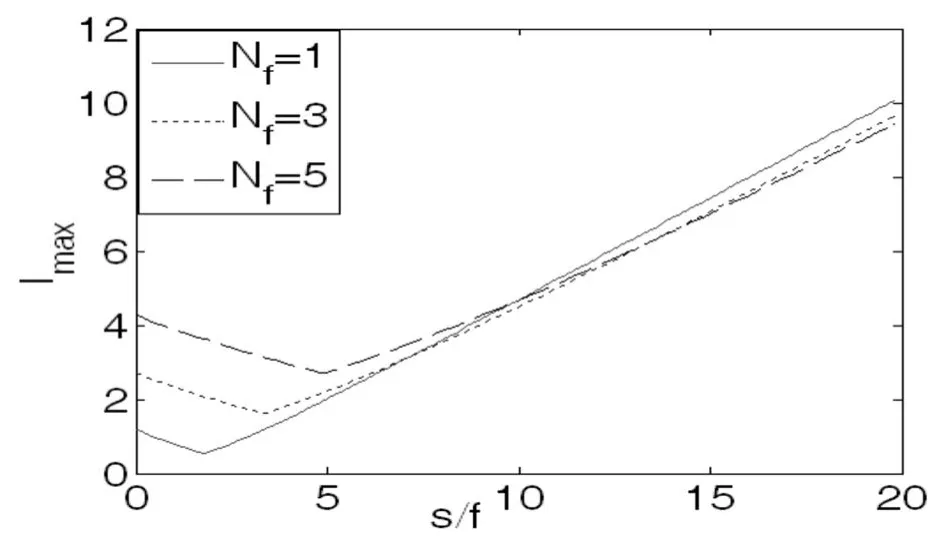
Fig.5 Axial maximum irradiaceImaxversus relative separations/f.a=0.5,b=2.0
4 Conclusions
In this paper,the focal shift and focal switch of EchGbeams passing through a sigle thin lens system has been studied in detail.It has been found that the axial irradiance distributionI(0,0,z)and maximum irradiance along the axisImaxdepend not only on the distance of aperture and lens but also on beam parametresa,band Fresnel numberNf.Moreover, whenais less than its critical maximum and b is grester than its critical maximun,there exist two axial intensity maxima,and the focal switch of EchGbeams can take place at the turning points/f.Additionally,for different Fresnel numberNf, the behavior of the focal shift and focal switch is different.Finally,we would like to mention that the focusing properties of EchGbeams in this paper are of both theoretical and practical interest,and may find some potential applications in the precise and variable focusing.
[1]Li YJ,Wolf E.Focal shifts in diffracted converging spherical waves[J].Opt Commun,1981,39(4):211-215.
[2]Li YJ,Wolf E.Focal shift in focused truncated gaussian beams[J].Opt.Commun,1982,42(3):151-156.
[3]Martínez-Corral.M,Climent.V.Focal switch:a new effect in low-Frensnel-number systems[J].Appl.Opt.,1996,35(1): 24-27.
[4]Li YJ.Focal shift and focal switch in dual focus systems[J].J.Opt.Soc.Am.A,1997,14(6):1297-1314.
[5]Tang B,Wen W.Focal shift and focal switch of flat-topped Mathieu Gaussian beams passing through an apertured lens system[J]. Opt.Commun,2009,282(12):2281-2285.
[6]Li J S,Gao X M,Zhuang S L,Huang C Q.Focal shift and focusing properties generation by radial cosine phase masks[J].Optik, 2010,121(9):821-825.
[7]Ghafary B,Siampoor H,Alavinejad M.Focal shift for off-axial partially coherent flat topped beams passing a thin lens[J].Optics& Laser Technology,2010,42(5):755-759.
[8]CaspersonL W,Hall D G,T ovar A A.Sinusoidal-Gaussian beams in complexoptical systems[J].J.Opt.Soc.Am.A,1997,14 (12):3341-3348.
[9]Du X Y,Zhao D M.Elliptical cosh-Gaussian beams[J].Opt Commun,2006,265(2):418-424.
[10]K onar S,Mishra M,Jana S.Nonlinear evolution of cosh-Gaussian laser beams and generation of flat top spatial solitions in quintic nonlinear media[J].Phys.Lett.A,2007,362(5-6):505-510
[11]Chu X X.Propagation of a cosh-Gaussian beam through an optical system in turbulent atmosphere[J].Opt.Express,2007,15 (26):17613-17618.
[12]Banders M A.Elegant Ince-Gaussian beams[J].Opt.Lett.,2004,29(15):1724-1726.
[13]Deng D M,Guo Q.Elegant Hermite-Laguerre-Gaussian beams[J].Opt.Lett.,2008,33(11):1225-1227.
[14]April A.Nonparaxial elegant Laguerre-Gaussian beams[J].Opt.Lett.,2008,33(12):1392-1394.
[15]Collins.S.A.Jr.Lens-system diffraction integral written in terms of matrix[J].J.Opt.Soc.Am,1970,60(9):1168-1177.
[16]Tao X Y,Ji XL,Wang C F.Focal switch of astigmatic Hermite-Gaussian beams[J].Opt Commmun,2004,241(4-6):429-435.
[17]Ji XL,LüB D.Focal shift andfocal switchof Bessel-Gaussian beams passing through a lens systemwithor without aprtuer[J].Optics &Laser Technology,2007,39(3):562-568.
[18]Ji X L,LüB D.Focal switch of cosine-Gaussian beams focused by a thin lens without aperture[J].Laser Technology,2005,29 (6):654-656(in Chinese).
复宗量双曲余弦高斯光束的焦移和焦开关
文 伟1,2, 施振刚1,2, 邓晓鹏1,2
(怀化学院1.物理与信息工程系; 2.信息科学研究所,湖南怀化 418008)
由collins衍射积分,推导出了复宗量双曲余弦高斯 (EchG)光束通过无光阑透镜后的轴上光强分布公式和轴上最大光强位置满足的一元三次方程,得出了制约焦开关现象的解析条件.在此基础上作了大量的数值分析.结果表明,除了菲涅耳数外,相对入射距离和光束参数都影响焦开关.这些结果将有助于了解EchG光束的聚焦特性.
焦移; 焦开关; 复宗量双曲余弦高斯光束; 无光阑透镜
2010-03-26
湖南省教育厅资助科研项目 (No.07C506);怀化学院资助科研项目 (No.HHUQ2009-07).
文 伟 (1978-),男,湖南张家界人,怀化学院讲师,硕士,主要研究激光束的传输与变换.

