Stability of Improved Semi-implicit Milstein Methods for Stochastic Differential Equations
LI Qi-yong
(Department of Mathematics,Huaihua University,Huaihua,Hunan 418008)
Stability of Improved Semi-implicit Milstein Methods for Stochastic Differential Equations
LI Qi-yong
(Department of Mathematics,Huaihua University,Huaihua,Hunan 418008)
Abstract:This paper gives investigation of mean-square and asymptotic stability of improved semi-implicit Milstein methods for stochastic differential equations.It is shown that the improved semi-implicit Milstein methods recovered the mean-square stability properties of the linear test equation,if and only ifFor asymptotic stability,we proved that the methods can reproduce the stability of the test problem provided that the stepsize is sufficiently small.
Key words:semi-implicit Milstein methods; stochastic differential equations; mean square stability; asymptotic stability
CLC number:O211.63 Document:A Article ID:1671-9743(2012)05-0001-06
1 Introduction
Consider an Ito autonomous scalar stochastic differential equation
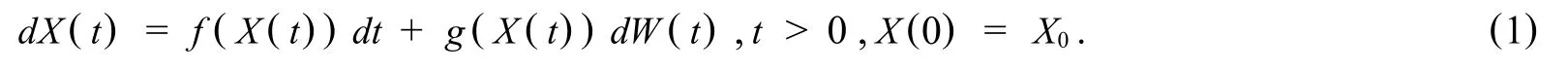
driven by the standard Wiener process W(t).In recent years,there are extensive literature on the numerical simulation for SDEs(1),for example,[1-10]and the references therein.The semi-implicit Milstein(SIM)methods[7]for computing approximationsXn≈ X(tn),withtn=nΔt,takes the form
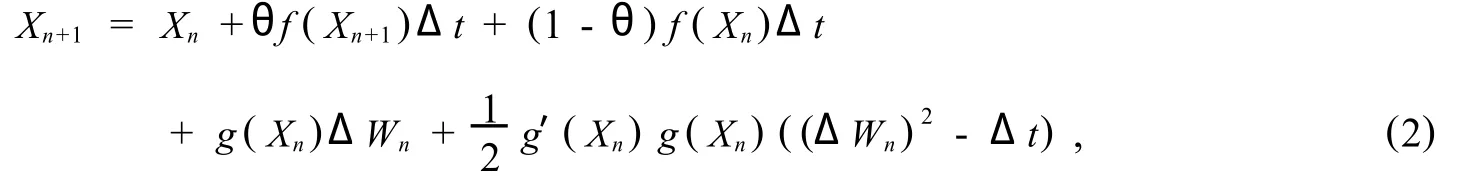
In[7],Higham studied mean-square stability of the SIM methods(2),and derived that the SIM methods recover the mean-square stability property of the linear test equation if the parameterθis increases beyond its normal range,i. e.
We can represent(2)in the form

By introducing the implicit in the terms includingΔt,we have the following improved semi-implicit Milstein(ISIM)methods
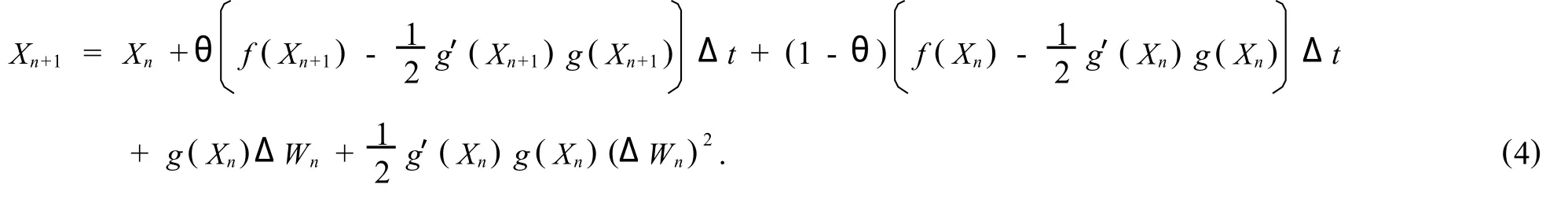
In this paper,we consider the mean-square and asymptotic stability properties of the ISIM methods(4).T o study the stability properties,we take the test equation withf(x)=λxandg(x)=μxin(1),so that
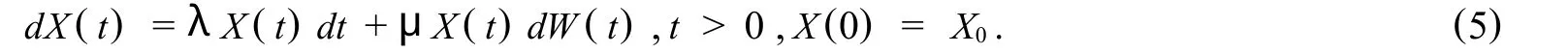
Hereλ,μ∈R,and we assume thatX0≠0 with probability 1.Solutions of(5)have the following properties
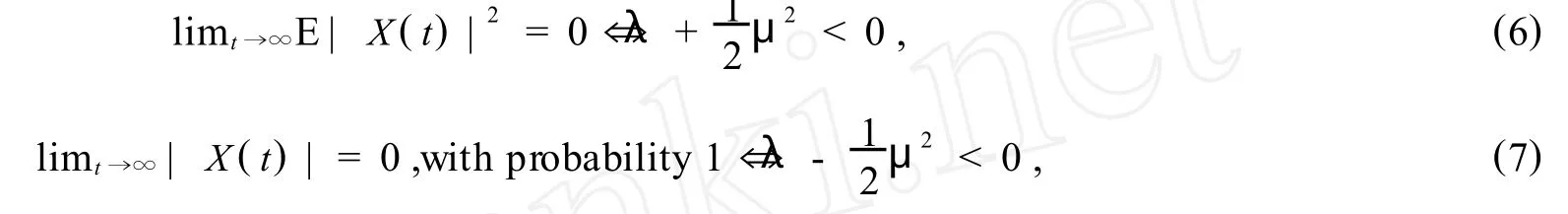
where E(·)denotes the expected value.The property on the left-hand side of(6)is known as mean-square stability,whereas the left-hand side of(7)defines asymptotic stochastic stability(in large)(hereafter,asymptotically stable).
Applying the ISIM methods(4)to the linear test problem(5),we get

Note that forθ>0,Xn+1is defined by an implicit equation.However,Xn+1is well-defined if(6)or(7)holds.
2 Mean-square stability of ISIM methods
By analogy with the definition for the SDE(5),we will say that the sequence(8)is mean-square stable if limn→∞E|Xn|2=0.Note that the ISIM methods depend upon the problem parametersλ,μ,and the method parameters θandΔt.For a particular choice of these parameters,we will say that the ISIM methods are mean-square stable if they produce a mean-square stable sequence.
(1)The ISIM methods(8)are mean-square stable for anyΔt>0,if and only if

Proof Rewriting(8)gives
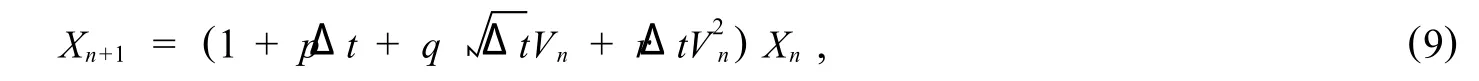
Where
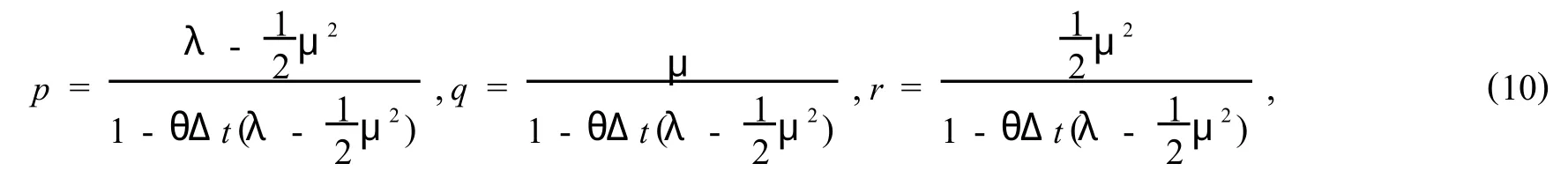
and eachVnis an independent Normal(0,1)random variable.Here we assume thatwhich is naturally satisfied provided thatSquaring both sides in(9)and taking the expected value,we have

Hence,the methods are mean-square stable if and only if
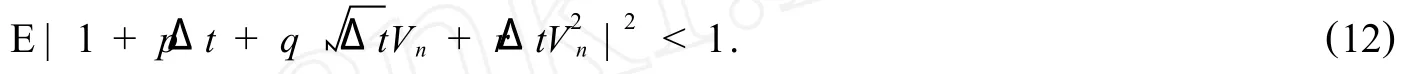
By the identities
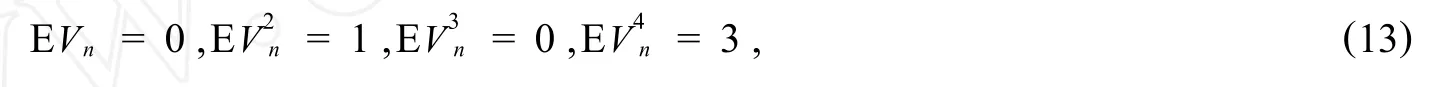
we derive that(12)is equivalent to



Here,θ2+4θ-1>0 by the factNoting thatwe then derive that the first term in the right-hand side of(16)is positive.Sincepromisesit follows that

Now,we turn to the case0≤θ<1/2.By takingμ=0(deterministic ODE),then(6)and(14)reduce toandrespectively.In this case,although the problem is stable,the method is not stable for
The proof is completed.
In order to visualize the stability regions,we will draw these pictures in thex-yplane,wherex=Δtλandy= Δtμ2.In this way,given problemparametersλandμ,varyingΔtcorresponds to moving along a ray that passes through the origin and(λ,μ2).The following result is immediate from(14).
Theorem 2 The ISIM methods(8)are mean-square stable if and only if
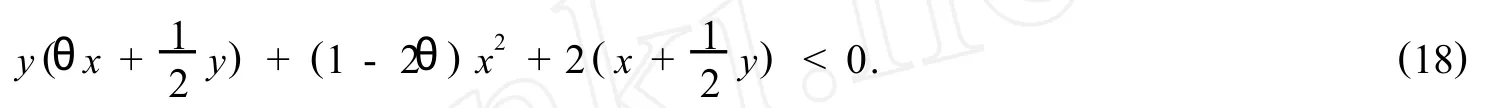


Figure 1 Boundary of mean-square stability region for the test problem(solid line)and the methods(dashed line)
Figure 1 gives the boundary offor,1,in dashed line.The boundary2x+y=0of the SDE stability region is also plotted with solid line.From Figure 1,we know that theregions increase monotonically withθ.Whenlies inside the region below black solid curve and is strictly contained inWhenthe upper boundary ofis formed by two separate branches of a hyperbola andin the left half planeis still strictly contained indegenerates to the wedge2x+y=0 in the left half plane and the wedgein the right half plane.Forθ=1is strictly contained inThese observations are consistent with the conclusions of Theorem 1.
3 Asymptotic stability of ISIM method
By analogy with the definition for the SDE(7),we will say that the sequence(8)is asymptotically stable ifwith probability 1.For a particular choice ofλ,μ,Δtandθ,we will say that the ISIM method is asymptotically stable if it produces an asymptotically stable sequence.
By Lemma 5.1 in[6],the sequence(8)is asymptotic stability if and only if
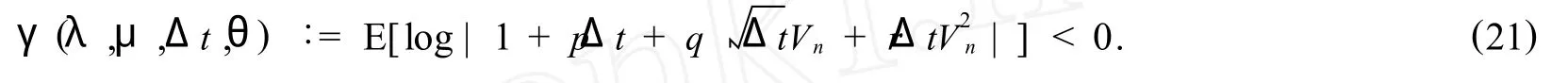
Hence,the asymptotic stability issue reduces to the study of the expected value of a random variable.
Proof By(21),we have

Recalling the fundamental inequality

we derive that
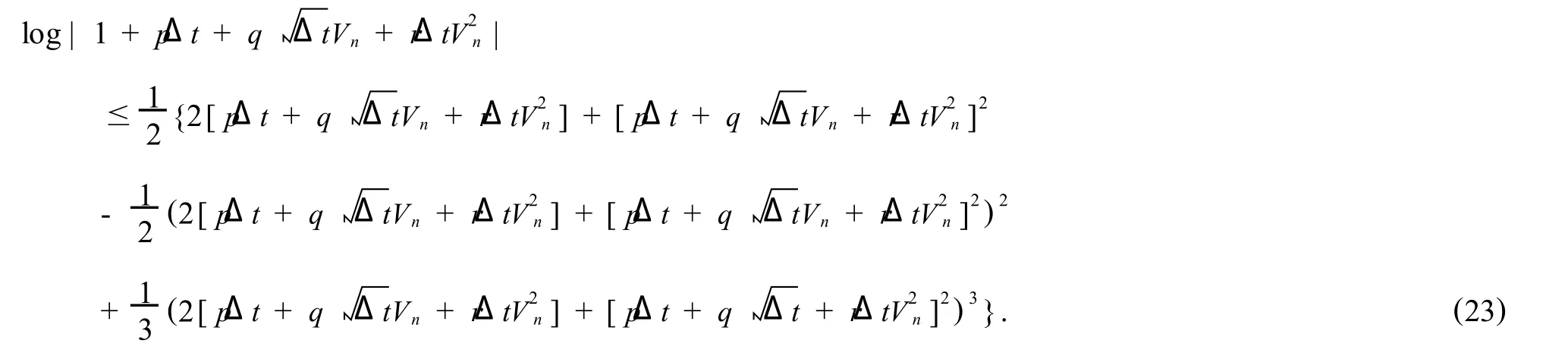
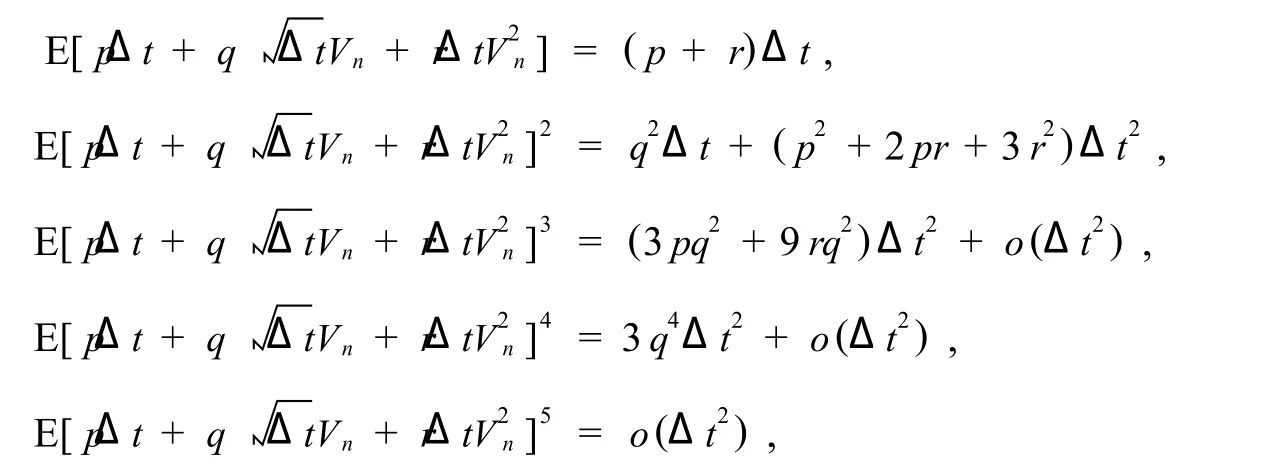

Taking expectation in(23)and using(24),we obtain

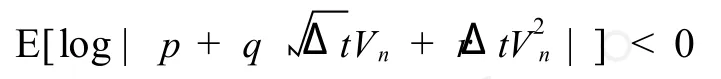
always holds.The poof is completed.
[1]K loeden P E,Platen E.Numerical Solution of Stochastic Differential Equations[M].Berlin:Springer,1992.
[2]Milstein GN,Tretyakov M V.Stochastic Numerics for Mathematical Physics[M].Berlin:Springer,2004.
[3]Platen E.An introduction to numerical methods for stochastic differential equations[J].Acta Numer.1997,8:197-246.
[4]Higham D J,Mao Xuerong,Stuart A M.Strong convergence of Euler-type methods for non-linear stochastic diffrential equations[J]. SIAMJ.Numer.Anal.2002,40:1041-1063.
[5]Saito Y,Mitsui T.Stability analysis of numerical schemes for stochastic differential equations[J].SIAMJ.Numer.Anal.1996,33: 2254-2267.
[6]Higham D J.Mean-square and asymptotic stabilityof the stochastic theta method[J].SIAMJ.Numer.Anal.2000,38:753-769.
[7]Higham D J.A-stability and stochastic mean-square stability[J].BIT.2000,40:404-409.
[8]Higham D J,Mao Xuerong,Stuart A M.Exponential mean-square stability of numerical solutions to stochastic differential equations [J].LMSJ.Comput.Math.2003,6:297-313.
[9]Wang Zhiyong,Zhang Chengjian.An analysis of stability of Milstein method for stochastic differential equations with delay[J].Comput. Math.Appl.2006,51:1445-1452.
[10]Buckwar E,Sickenberger T.A comparative linear mean-square stability analysis of Maruyama-and Milstein-type methods[J]. Math.Comput.Simulation.2011,81:1110-1127.
随机微分方程改进半隐Milstein方法的稳定性
李启勇
(怀化学院数学系,湖南怀化 418008)
研究了随机微分方程改进的半隐Milstein方法的均方稳定和渐近稳定性.对线性检验方程,得到了改进的半隐Milstein方法对任意步长Δt>0均方稳定的充要条件是证明了当方法的步长充分小时,方法能保持原系统的渐近稳定性.
半隐Milstein方法; 随机微分方程; 均方稳定; 渐近稳定
2012-04-20
湖南省教育厅青年项目 (11B095).
李启勇 (1977-),湖南武冈人,怀化学院讲师,博士生,主要研究随机微分方程数值解.
——丘成桐

