基于互信息量的改进K-Modes聚类方法

吴润秀

（南昌工程学院计算 机系，南昌 330099）

0 引言

聚类算法常被称为一种无监督的学习方法，聚类分析是数据挖掘中的主要技术之一，聚类分析是根据组内相似度高，组间相似度低的原则将数据对象进行分类。在聚类过程中一个关键问题就是相似性度量的定义,当数据对象的每个特征均是数值型(实数,整数)时,相似性度量的定义有诸多选择,因为此种情形每个数据对象可用n维空间中的向量来表示(n为特征个数),则n维空间的距离(如欧氏距离,马氏距离,范数距离等)可用来定义对象之间的相似度,且这些度量只仅仅依赖特征向量之间的差值.然而在数据挖掘的应用中,有诸多数据对象是用类型数据来描述的,这使得我们不能通过计算两个特征向量值之差来表示对象之间的距离,最简单的办法是overlap,即若两个对象的属性值相等则为1，不相等则为0，这种简单匹配方法没有把整个数据集考虑进来，Boriah等[2]对类型数据的相似性度量做了较详细的综述和分析，分析了14种相似性度量及其在聚类中的优缺点，这14种相似性度量方法都只考虑了用同一属性值的分布特征来修正属性值之间的相似度，没有考虑数据对象属性之间的相互关系对相似度的影响，白亮等[6]通过用粗糙集中的上下近似集来定义两个属性值之间的距离,张小宇等[7]通过连接度来定义两个属性值之间的距离,Dino Ienco等[1]应用条件概率差来定义两个属性值之间的距离,他们的实验结果表明均能提高类型数据的聚类效果,但这些方法都涉及到一个计算复杂度高的问题.我们在本文中提出一种用样本互信息来刻画数据对象属性之间的相互关系,每两个数据对象之间的距离是由其各个属性值之间的距离决定,每两个数据对象属性值之间的距离又是由其他属性值之间的距离来确定,一个属性对另一个之间的距离影响程度是由互信息来决定的。由此我们可定义综合整个数据对象的信息和每个数据对象个体信息的类型数据对象之间距离的度量方法(由此也可定义相似度)。

本文提出的距离度量方法，其算法复杂性低,在UCI数据集上的实验表明,与传统k-modes方法比较,有效地提高了聚类精度。

1 K-modes聚类方法[3-4]

1.1 K-modes聚类方法概述

令 X1=(x11,x12,…,x1s),X2=(x21,x22,…,x2s)是两个对象，有s个字符属性(即categorical data)，则 X1,X2之间的差异性度量为：

假设有p个对象的类C={X1,X2,…Xp}，Xi=(xi1,xi2,…,xis),(1≤i≤p)，它的Modes（众数）Q={q1,q2,…qs}，其中qj是{X1j,X2j,…,Xpj}的众数。

则n个对象分成k类的最优化问题为：

1.2 K-Modes聚类算法

k-modes算法是对k-means算法的扩展。k-means算法是在数据挖掘领域中普遍应用的聚类算法，它只能处理数值型数据，而不能处理分类属性型数据。例如表示人的属性有：姓名、性别、年龄、家庭住址等属性。而k-modes算法就能够处理分类属性型数据。k-modes算法采用差异度来代替k-means算法中的距离。k-modes算法中差异度越小，则表示距离越小。一个样本和一个聚类中心的差异度就是它们各个属性不相同的个数，不相同则记为1，最后计算1的总和。这个和就是某个样本到某个聚类中心的差异度。该样本属于差异度最小的聚类中心。具体步聚如下：

第一步:给定含有n个对象的数据集T和聚类数k。

第二步：随机选择k个对象Xi(1≤i≤n)作为初始众数Q1,Q2,…,Qk，每一个成为一类。

第三步：利用公式（1）计算所有对象与上述k个初始众数的差异性度量d(Xi,Qj)(1≤i≤n,1≤j≤k)，然后将每个对象分配到与其差异性度量最小的那个类当中，得到k个分类C1,C2,…,Ck。

第四步：重新计算每个类的众数Q1,Q2,…,Qk。即在每个类中，对每个属性选取在该类中所占比例最大的属性值作为该类的众数的属性值。从而得到每个类的众数Q1,Q2,…,Qk。

第五步：返回到第三步，直到每个类的众数不再发生改变为止。

2 互信息的相关概念

在信息论中,熵是随机变量的不确定性度量或自信息的平均值。一个随机变量X的熵是该随机变量X所含信息量的度量。设随机变量X=[x1,x2,…,xs],p(xi)(1≤i≤s)是随机变量X的分布列，则随机变量X的信息熵可定义为:

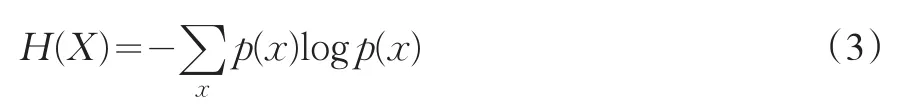
联合熵是指一对变量X和Y的不确定度,即两个随机变量X和Y的联合熵(Joint Entropy)定义为:

互信息(Mutual Information)是另一有用的信息度量，它是指两个随机变量之间的相关性。两个随机变量X和Y的互信息定义为：

其中当X和Y是离散型随机变量时,p(x,y)表示的是X,Y的联合分布列,p1(x),p2(y)分别是X,Y的边缘分布列,当X和Y是连续型随机变量时,X和Y的互信息为：

此时 p(x,y)是X,Y的联合密度函数,p1(x),p2(y)分别是X,Y的边缘密度函数。

性质1:I(X,Y)=H(X)+H(Y)-H(X,Y)

性质2:I(X,X)=H(X)

性质3：I(X,Y)=I(Y,X)

性质4：I(X,Y)≥0

性质5：如果X与Y互相独立，则I(x,y)=0

3 基于样本互信息量的改进K-Modes聚类算法

3.1 基于互信息量的对象之间的距离公式

定义S=(U,A)为一个信息系统，U={x1,x2,…xn}为对象全体，A={A1,A2,…Am}为属性集，数据如表1所示：

表1 数据表

I(Ai,Aj)(i,j∈{1,2,…,m}）表示属性 Ai与 Aj的互信息，当i=j时，I(Ai,Ai)=H(Ai)就是属性 Ai的信息熵，定义对象xi和xj的第k个属性之间的差异性度量为：

性质6:两个对象 xi和 xj的属性值完全相同时,则d(xi,xj)=0

性质7:两个对象 xi和 xj的属性值完全不相同时,则d(xi,xj)=1

3.2 基于样本互信息的改进K-Modes聚类算法

在基于互信息量的对象之间的距离公式的基础上，我们得到基于样本互信息的改进K-Modes聚类算法如下：

第一步:给定含有n个对象的数据集T和聚类数k;

第二步:任意给出T的k个非空子集C1,C2,…Ck(C1⋃C2…⋃Ck=T)作为初始的聚类划分；

第三步：计算目前划分C1,C2,…Ck的众数Ql={ql1,ql2,…qls}(l=1,2,…,k)。即在每个Ci(1≤i≤k)类中，对每个属性选取在该类中所占比例最大的属性值作为该类的众数的属性值,从而得到每个类的众数Q1,Q2,…,Qk。

第四步：对每一个对象xi(1≤i≤n)，利用公式8计算到k个众数Ql（1≤l≤k）的距离d(xi,Ql)，并将 xi分配到距离最小的众数所在的类。得到新的划分C1,C2,…Ck;

第五步：返回第三步,直到每个对象所属类不再改变为止。

4 实验分析

为了评价一种聚类算法质量，通常是一件很难又带有主观性的工作。因此我们引入了两个客观标准来评价聚类的结果：精度（Accuracy）和标准互信息（Normalized Mutual Information）。

聚类的标准互信息定义为：

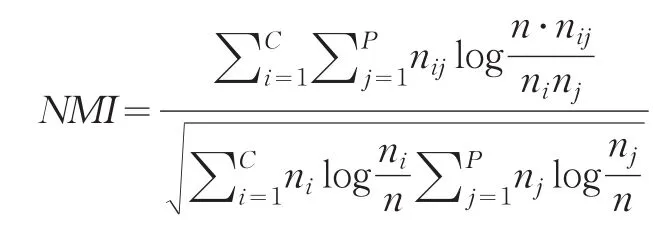
其中nij是既出现在聚类i中，同时又出现在分类j中的对象集合的关联基数；ni是在聚类i中的对象数；nj是在分类j中的对象数；n是数据集中总的对象数。C和P分别表示聚类数和分类数。NMI可用来计算任意一对聚类与分类之间的平均互信息，NMI的值越高，聚类结果越好。

为了测试该算法的有效性,我们从UCI数据集中挑选了2组数据进行实验,分别为vote和mushroom,2组数据描述如表2所示。

表2 数据描述

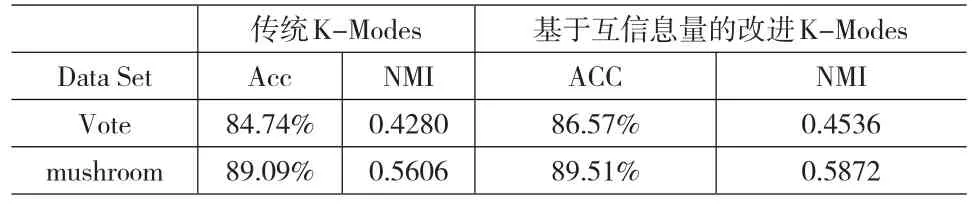
表3 在2种不同数据集下算法精度和NMI的比较

在表3中，我们列出了基于互信息量的改进K-Modes聚类算法与传统的K-Modes聚类算法分别运行在Vote和mushroom两个数据集上相比较评价的结果。通过表3可知，几乎在所有的实验中，不管是在Vote数据集上，还是在mushroom数据集上，基于互信息量的改进K-Modes聚类算法不仅在聚类精度上比传统的K-Modes聚类算法结果更好，而且在聚类的平均标准互信息上也比传统的K-Modes聚类算法结果更好，表明基于互信息量的改进K-Modes聚类算法有效地提高了聚类效果。

5 结束语

本文引入样本互信息的方法，提出了一种新的距离度量，该距离度量方法算法复杂性低,且该距离公式既考虑了对象某个属性值本身的不同，又考虑了对象其它属性对该属性值的影响，使之更符合实际问题情况。通过在UCI数据集上的实验，与传统的K-Mode聚类算法进行了比较，实验结果表明，基于互信息量的改进K-Modes聚类算法有效地提高了聚类精度。

[1]Dino Ienco,Ruggero G.Pensa,Rosa Meo.Context-Based Distance Learning for Categorical Data Clustering[Z].IDA 2009,LNCS 5772,2009.

[2]Shyam Boriah,Varun Chandola,Vipin Kumar.Similarity Measures for Categorical Data:A Comparative Evaluation[EB/OL]＜Sboriah,Chando⁃la,Kumar＞@cs.umu.edu,1999.

[3]Amir Ahmad,Lipika Dey.A K-mean Clustering Algorithm for Mixed Numeric and Categorical Data[J].Data&Knowledge Engineering,2007,（63）.

[4]Michael K.Ng,Mark Junjie Li,Joshua Zhexue Huang,Zengyou He.On the Impact of Dissimilarity Measure in k-Modes Clustering Algorithm[J].Ieee Transactions on Pattern Analysis and Machine Intelligence,2007,29(3).

[5]Amir Ahmad，Lipika Dey.A Method to Compute Distance between Two Categorical Values of Same Attribute in Unsupervised Learning for Categorical Data Set[J].Pattern Recognition Letters，2007，（28）.

[6]白亮,梁吉业,曹付元.基于粗糙集的改进K-Modes聚类算法[J].计算机科学,2009,36(1).

[7]张小宇,梁吉业,曹付元,于慧娟.基于加权连接度的改进K-Modes聚类算法[J].广西师范大学学报自然科学版,2008,26(3).