色谱经济分析法塔板理论的换例模拟
沈 萍,乔 杨,陈琪瑶,游士兵
(1.武汉职业技术学院,武汉 430074;2.武汉大学,武汉 430072)
0 引言
将化学领域中的色谱分析法引入人文社会科学领域,对复杂经济现象系统进行分离、定性和定量分析的可行性,以及色谱经济分析法原理的基础研究在游士兵等发表的论文《复杂经济现象分类方法创新的理论前瞻——基于化学“色谱分析法”的借鉴与思考》和《色谱分析原理在经济领域应用基础研究——以金融证券投资和快速消费品行业为例》中已经进行了阐述。在游士兵等发表的论文《色谱经济分析法置换系列研究:塔板理论》中也对色谱经济分析法之塔板理论进行了详细地阐述,本文将不在赘述。
由于社会经济系统属于非线性开放的系统,经济事件与现象背后存在着大量的外生变量,具有很强的随机性,目前还很难建立统一的客观标准对各类企业在不确定性下的行为进行分类研究。因此,本文将以面临价格不确定性下的企业行为为例,尝试应用色谱经济分析法之塔板理论对不同类型混合企业群进行分类和定性分析,一方面为了验证塔板理论的有效性;另一方面想通过换例研究更进一步凝练塔板理论在色谱经济分析法中的应用基本规则。
1 研究对象
以200家同质的混合企业群为研究对象,假定所有企业生产同一种永续畅销品(如盐),该产品的需求弹性较小,企业为保证每期之间的产品销售顺利衔接、预防不确定因素的冲击等,必须保留适量的库存,并且保留一定的库存不会给企业带来产品积压的压力,企业对其生产的产品可做出销售或库存两种处理方式。
由于企业在市场经济的环境下,有着充分的经营自主权,可以即时根据市场需求、企业发展需求等情况的变化调整企业的生产规模、产品类型、产品数量以及库存量等。由于企业个体自身各方面的差异,不同的企业即使面对相同的市场信息也会表现出不同的应对行为。
2 应用色谱经济分析法之塔板理论模拟分离
2.1 模拟分离的基本假设
假定1在一定期间内(t~t+1时期内),混合企业群中每个企业的生产总规模都保持不变,且有无限次等量产品的均匀增加,即每批新生产的产品数量保持不变,假定所有待分离企业每批新生产的产品数量为100个单位。
假设2假定在面临价格变化时,所有企业有能力决定自己的销售量与库存量的变化。
假定3假定200家同质的混合企业群中只有两类不同企业,各占一半,即A类企业100家,B类企业100家。其中A类企业在t时期预测其所生产的产品价格将在t+1时期出现上升的情况时,为增加其在t+1期的销售利润,选择将新一批次生产的产品在t+1期全部销售的企业数量将增加。即如果t时期该类企业中决定将新一批次生产的产品作为库存的企业数量与决定将新一批次生产的产品进行销售的企业数量比为1:1,在预测产品价格将在t+1时期出现上升的情况时,该类企业中决定在t+1期将新一批次生产的产品作为库存的企业数量与决定将新一批次生产的产品进行销售的企业数量比由原来的1:1调整为1:4;而B类企业在t时期预测其所生产的产品价格将在t+1时期出现上升的情况时,仍然保持原有的销售与库存计划,不受产品价格波动的影响,那么选择将新一批次生产的产品在t+1期全部销售的企业数量将不变。即如果t时期该类企业中决定将新一批次生产的产品作为库存的企业数量与决定将新一批次生产的产品进行销售的企业数量比为1:1,在预测产品价格将在t+1时期出现上升的情况时,该类企业中决定在t+1期将新一批次生产的产品作为库存的企业数量与决定将新一批次生产的产品进行销售的企业数量比仍然保持为原来的1:1。
假设4如果将样本分类过程分为5个小段,即塔板数为5,在每一个塔板内,每个企业都可以对新一批次生产的产品做出销售或库存选择,并瞬间很快执行选择,达到分配平衡,整个分类过程就是经历多次的分配平衡的过程。
假定5假定两类企业各自的分配比(K’)在各个塔板上均为常数。
假定6样本分类过程中各个企业之间互不影响。
2.2 模拟分离过程的分析
该分离过程中,固定相设置为企业选择将新一批次生产的产品作为库存的倾向;流动相设置为企业选择将新一批次生产的产品进行销售倾向;脉冲设置为企业无限次等量产品的均匀增加量(100个单位);分配比即为选择将新一批次生产的产品作为库存的企业数与选择将新一批次生产的产品进行销售的企业数之比。
因此根据以上基本假设可知,样本中A类企业在面临产品价格即将上升的情况时,其分配比由1:1调整为1:4;而B类企业在面临产品价格即将上升的情况时,其分配比保持不变,仍然为1:1。
在企业在预测其所生产的产品价格将出现上升的情况时,将样本“注入”色谱柱,开始对200家同质的混合企业群进行分离与分析。由于A类企业在面临产品价格即将上升的情况时,分配比为1:4,所以100家A类企业在进入色谱柱后的表现为:0号塔板处企业数总量为100,当第一个脉冲进入色谱柱后,即第一次增加100单位产品时,20家企业选择将增加的100单位的产品作为库存,即留在原塔板,80家企业选择将增加的100单位的产品进行销售,即前进到1号塔板;第二次再增加100单位产品时,0号塔板中的企业再次对将增加的100单位的产品做出库存或销售的选择,选择被执行后,即达到分配平衡时,仍然有1/5的企业选择库存,4/5的企业选择销售,则0号塔板里的企业数变为4;同样1号塔板中的企业也面临着销售或库存的选择,达到分配平衡后,有32家企业选择中留守在1号塔板,64家企业前进到2号塔板……以此类推,在经历了若干次脉冲后,在色谱柱出口统计“流出”的企业数就会出现状态发布的规律,如表1所示。

表1 A型企业在色谱柱内的分配情况
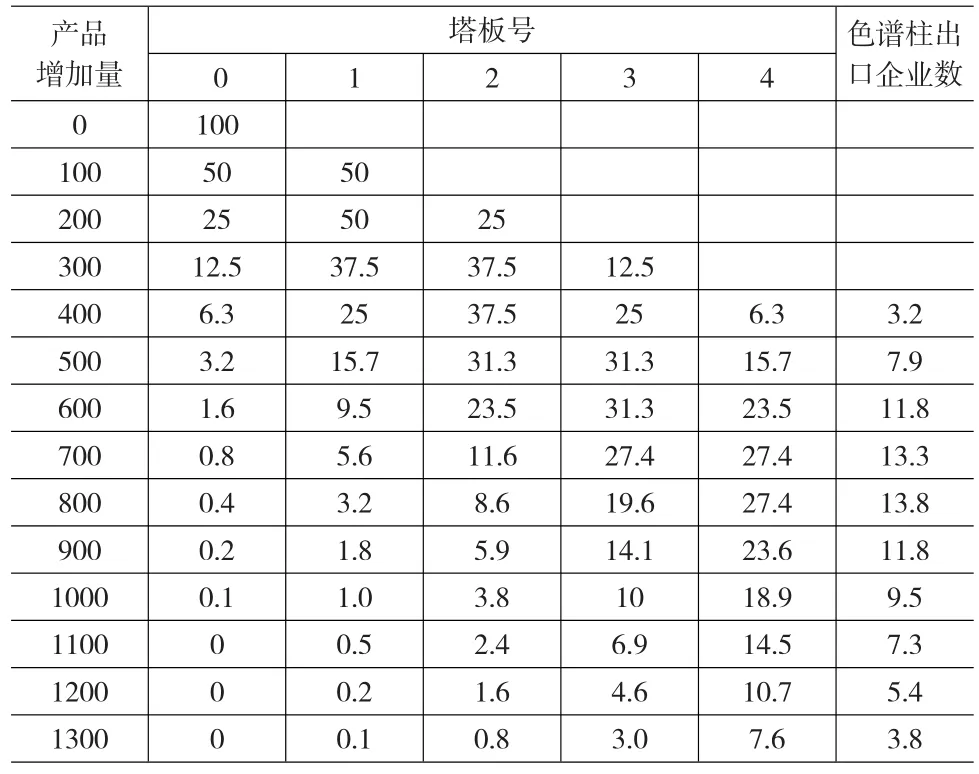
表2 B型企业在色谱柱内的分配情况
同理,由于B类企业在面临产品价格即将上升的情况时,分配比仍然为1:1,所以100家B类企业在进入色谱柱后的表现如表2所示。
2.3 模拟分离结果讨论
以色谱柱出口企业数作为纵坐标,产品增加量作为横坐标,将表1和表2绘制为图,可以得到色谱图,见图1。

图1 200家同质的混合企业群分离色谱图
从色谱图中可以看出,由于分配比不同,同质的混合企业群经过色谱柱后,会得到两个不同的峰。每个峰的色谱柱出口最大企业数不同,每个峰的色谱柱出口最大企业数所对应的产品增加量也不同,即,每个峰的峰高(色谱柱出口最大企业数)和保留时间(产品增加量)都不同,而每个不同的峰对应着一个不同类型的企业。其中,A型企业在产品增加量达到600(保留时间)时,出现其色谱峰值39.3(峰高);而B型企业在产品增加量达到800(保留时间)时,出现其色谱峰值13.8(峰高)。因此,可以根据图1所示,通过在不同的保留时间段(不同的产品增加量)“收集”色谱柱出口“流出”的企业,以实现将混合企业群中不同类型的企业进行分离的目的。但是从图1中也可以看出两个不同类型的企业对应的两个色谱峰不是完全的正态分布,也没有完全分离,仍然有相当的部分出现交叉现象,这是因为设定的理论塔板数为5,若将设置的理论塔板数增加到100以上时,色谱峰就可以趋近于正态分布曲线了,而且在其他分离条件不变的情况下,增加理论塔板数,每个色谱峰的保留时间不会改变,但峰宽会变窄。当理论塔板数增加到一定的数量时,流出曲线中不同类型的企业对应的色谱峰就不会再出现峰交叉现象了。此时再在不同的保留时间段(不同的产品增加量)“收集”色谱柱出口“流出”的企业,就可以将混合企业群中不同类型的企业完全分离。
3 应用色谱经济分析法之塔板理论模拟分离的现实意义
3.1 不同经济现象内在的本质特性的不同是色谱经济分析法完成分离的根本原因
应用色谱经济分析法对复杂经济现象进行分离的关键在于流动性与固定相的选择,流动性与固定相的选择原则是根据组分的特性,选择合适的固定相和流动相,使得不同组分与两相间的“作用力”——“吸附”与“解吸”力,这种“作用力”对外表现为不同组分在两相间的分配比不同,这也是混合样本在“流出”色谱柱后实现各组分分离的根本原因。可见,色谱经济分析法对复杂经济现象进行分类和分析的利用的是不同经济现象内在的本质特性的不同。
3.2 增加理论塔板数,可改善分离效果
进入色谱柱后被分离混合样本在“流过”每一个塔板时,都会在固定相和流动相之间完成一次分配平衡。如果保持固定相和流动相不变,而仅仅是增加有效理论塔板数,例如增加色谱柱的长度等,可以使得被分离混合样本在两相间完成的分配平衡次数越多,那么混合样品中各组分的特性的微小差距就可以被放得更大。当混合样品中各组分分配比的微小差距被放得足够大时,混合样品中不同分配比的组分在经过色谱柱的分离后,检测柱口“流出”情况,可以得到与不同组分相对应的、彼此分离的,并且具有不同的峰高和保留时间的不同色谱峰。通过在不同的保留时间段收集色谱柱出口流出的组分,就可以实现混合样品中不同组分的完全分离。而经济学领域中的应用色谱经济分析法对其他复杂经济现象进行分类和分析的时候,理论塔板数的大小具有无穷大的潜力,因此可以保证用色谱经济分析法对其他复杂经济现象进行分类的分离效果。以上分离过程的模拟尝试进一步证明了将色谱分析法的塔板理论应用到经济学中的可操作性;同时也为在经济学领域中应用色谱经济分析法对其他复杂经济现象进行分类和分析提供了指导。
3.3 有效分离为进一步的个体分析打下基础
以上分离过程模拟基本实现了对不同类型混合企业群的有效分离,在此基础上则可以针对分离后的各个组分进行定性分析。由图1可知,A型企业的保留时间为600,这表明A型企业受固定相的“吸附力”较小,其选择库存的倾向更低,因此会“更早”地流出色谱柱。分析这一特点说明,A型企业当面临价格上升冲击时选择销售获利,即A型企业生产与销售行为更容易受市场波动的影响,属于灵活机动型企业,该类企业出现产品投机行为的原因可能是其销售渠道或客源的不稳定、企业规模较小、企业管理更具有灵活性、企业对市场反应更灵明和企业更看重短期利益等。同理,B型企业的保留时间为800,这表明B型企业受固定相的“吸附力”较大,其选择库存的倾向更高,因此会“较晚”地流出色谱柱。分析这一特点说明,B型企业当面临价格上升冲击时选择保持原有生产与销售行为,即B型企业生产与销售行为不容易受市场波动的影响,属于稳定型企业,该类企业对市场变化不做出反应的原因可能是其销售渠道或客源的稳定、企业规模较大、企业管理模式灵活性不足、企业对市场反应迟钝和企业不看重短期利益等等。可见,应用色谱经济分析法对混合企业群进行有效分离,不仅可以达到分类的目的,同时还可以根据保留时间的大小值对相应的企业类型进行定性分析,即利用色谱柱实现组分的分离与定性分析,充分挖掘出企业背后的信息,为针对不同类型企业实现做大做强提出战略指导建议打下基础。这对于实际应用有非常意义,也具有经济学领域现有的其他分类法所无法比拟的优点。
[1]詹益兴.实用色谱法[M].北京:科学技术文献出版社,2008.
[2]苏立强.色谱分析法[M].北京:清华大学出版社,2009.
[3]达世禄.色谱学导论[M].武汉:武汉大学出版社,1999.
[4]游士兵,吴比,沈萍,梅敏,苏正华.复杂经济现象分类方法创新的理论前瞻——基于化学“色谱分析法”的借鉴与思考[J].统计与决策,2011,(7).
[5]游士兵,梅敏,吴比.色谱分析法在经济领域中的应用展望[J].统计与决策,2011,(11).
[6]沈萍,张佩,毛锴苑,李跟强,游士兵.色谱经济分析法置换系列研究:分配比[J].统计与决策,2011,(9).
[7]陈剑,冀京秋,陈宝国.我国射频识别(RFID)技术发展战略研究[J].科学决策,2010,(1).

