基于伴随算子的大飞机气动布局精细优化设计
吴文华,范召林,陈德华,覃 宁,孟德虹
(1.中国空气动力研究与发展中心空气动力学国家重点实验室,四川 绵阳 621000;2.中国空气动力研究与发展中心高速空气动力研究所,四川 绵阳 621000;3.谢菲尔德大学,英国 谢菲尔德S3 7JJ)
0 引言
在飞行器气动布局设计的后期,布局的主要特征参数和外形都已经确定,比如机身的长度、圆柱段直径、机翼的展弦比、前缘后掠角、根梢比、截面最大厚度,机翼面积,尾翼位置及面积等。在这个时期,这些参数都已经成为其他学科设计的依据,主要气动性能也不宜有大的变动,以免全部设计工作推倒重来,因为这将带来巨大的经济损失并大大拖延进度。这时候的优化设计,可以对布局进行一些局部的、细节的调整,在不对其他学科设计造成较大的影响的前提下,进一步提高布局气动性能,比如减阻,降低巡航力矩等。调整布局的局部曲面形状,可以满足这个要求。对布局的局部曲面形状进行微调必然是多参数的以达到设计目的,只有设计参数达到足够的数量,才能够对曲面进行足够精细的调整。这种布局曲面的细致调整也将使得曲面微调引发的布局性能变化很小,比如一次调整导致的阻力变化有可能在1阻力单位以内。然而1个阻力单位,对于大飞机等巡航距离很远的飞行器仍然具有很大的意义。在优化过程中分辨这么小的阻力变化量,是对优化软件中流场解算数的极高要求,必须在网格密度、网格拓扑结构、差分格式等方面进行精心的设计、试验和调整才能做到。同时,由于参数多,使得曲面形状的变化多种多样,也会导致目标函数与设计参数之间形成复杂的函数关系,这种关系极有可能是非凸的、多极值的,这就使得传统的牛顿法、二次规划寻优算法效果变差,甚至无法使用。太多的参数又使得遗传算法、响应曲面算法、粒子群算法等全局寻优算法无法直接使用,需要探索新的,能够适应气动布局设计后期多参数精细优化设计需要的新型寻优算法。
由于数值计算非常耗时,在数值优化技术发展的最初阶段,设计参数的数量通常很少,这是因为不论采取哪种优化算法,优化设计的计算量都随着设计参数的增多而急剧增长,使得参数太多的优化问题根本无法完成。这一状况直到基于伴随算子的敏感导数解算方法出现才得到改观。敏感导数是指优化目标对设计参数的导数,可用于指导设计参数往哪个方向调整,以迅速获得最优结果。这种方法可以一次性求出所有敏感导数,计算精度高,计算时间随着设计参数的增加不会明显增多。伴随算子求导技术结合基于敏感导数的寻优算法,就可以完成极多参数的气动布局优化设计,有可能快速并准确地获得限定条件内的最优布局,而且该方法的计算量随设计参数数量的增多变化不大。
伴随算子求导技术在偏微分方程敏感导数求解中的应用至今为止已经超过30年。伴随算子的应用最早出现在控制优化中,随后在结构有限元优化中也有应用。在空气动力学领域中最先应用伴随算子技术的是Pironneau[1],之后美国的Jameson[2-4]将其应用到机翼的优化设计中。随后美国和西欧对基于伴随算子求导算法的气动布局优化技术进行了大量的研究[2-8],将伴随算子技术在气动优化设计中的应用大大拓展,比如飞行器全机气动布局的优化设计,最新的波音787、A380等飞机的研制中都应用了这项技术。
国内的气动布局优化设计研究,目前主要还集中在布局设计前期的少量主参数优化设计上,用于后期多参数高精度优化设计的研究很少。气动力的计算常用近似模型,无法满足精细优化设计的需要。
中国空气动力研究与发展中心总体技术部[9-10]、南京航空航天大学[11-12]和西工大[13-17]在基于伴随算子的多参数优化设计方面开展了一些研究,但是研究应用水平与西方发达国家相比还有差距,开展的多是翼型或者单独机翼的优化设计研究[11-17]。单独的机翼优化设计没能够考虑发动机或者机身对布局的影响,在布局设计后期的应用会受到限制。
目前的大型飞机布局大都采用机翼加柱形机身再加垂尾、平尾的布局方式。波音公司、空客公司的客机、运输机,从最早的波音737,到最新的A380、波音787,都采用了这种布局。经过了几十年的研究,这种布局的性能潜力已经得到了充分的挖掘,经过传统的设计手段的优化,其气动性能在给定设计条件下已经达到了相当高的水准。即使采用新的设计手段,受到布局形式的限制,其气动性能的提高也将很有限。国内外基于伴随算子的多参数优化设计算例,优化对象的初始气动特性大都较差,优化容易获得较大的性能提高。本文的优化对象已经经过传统设计手段的多轮优化,初始外形就具有很高的气动性能,对这种布局的优化难度大大提高。
本文以伴随算子优化方法为基础,发展了一套多参数、高精度优化设计软件,用于布局设计后期精细优化设计。该软件由雷诺平均N-S方程解算器、伴随方程解算器、动网格程序、二次规划寻优程序、外形参数化程序等构成。该软件系统在一种大型飞机布局全机构型的高精度优化设计中得到应用,优化过程中计入了短舱和机身等对机翼气动特性的影响,优化获得了良好的效果。
1 数值方法
常规的气动布局气动特性计算要求计算结果具有很高的精准度,虽然气动布局优化设计也要求计算结果准确,但是更强调优化过程中,不同布局外形气动特性——优化目标之间差量的准确性。如果计算过程中,解的振荡性太大,那么在解满足收敛条件时,有可能某个解在波峰,而另外一个解处在波谷,那么它们的差量就包含了较大的数值误差,因此本研究需要的解算器不仅要速度快,还要稳定性高,能很好地抑制解的振荡,以便数值误差互相抵消,获得高精度的差量。
用于优化设计的解算器还要具有很高的健壮性,即要求在求解过程中,最大限度地避免出现解不收敛等导致计算过程中断的情况出现,因为优化是完全自动进行的,期间要进行时间很长的迭代并且完成大量网格不同的数值计算,如果在其中的某一步出现问题,那么整个优化过程就会中断,或者导致错误的优化结果产生。
1.1 流场解算方法
根据优化设计平台对流场解算器的技术要求,在借鉴和改进国内外研究的基础上,采用基于黎曼近似基本解的Osher矢通量分裂格式和有限体积法方法来构造解算器[7],空间离散采用MUSCL 格式,时间离散采用隐式差分格式。这种方法具有较高的精度和良好的稳定性,同时能够有效抑制解的振荡,能够满足优化计算对数值解算器的几个要求。
任意控制体 上N-S方程组的积分形式为:
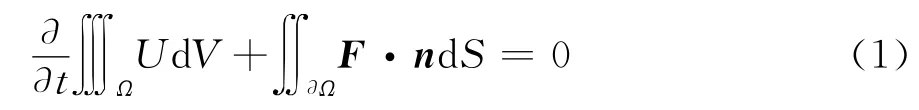
其中∂Ω表示控制体边界,F为N-S方程组除了时间项以外各计算项的矩阵形式[7]:
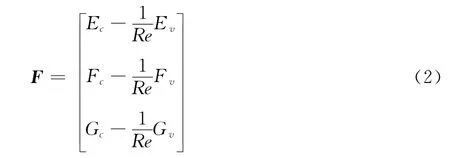
采用有限体积法将上述方程离散,意味着整个计算区域被分割成很多小的控制体,第i个控制体Vi上N-S方程组的形式为:

Ui为第i个控制体上状态变量的平均值,Ri为流经控制体表面的通量总和的残差矢量,

本计算程序是利用时间推进法求解稳态问题,对于第n个时间层,有:
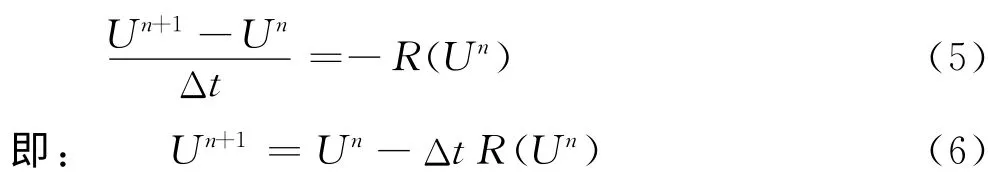
采用当地时间步长,以加速收敛。
对流项的处理采用近似黎曼解的Osher格式。Osher格式对间断问题的处理表现出色。由于采用有限体积法时,整个流场被划分为许多小控制体,每个控制体和周围相邻的某个控制体共享一个界面,通过计算每个界面上的通量来得到相邻控制体之间的影响,一旦每个控制体的变化得到,整个流场的变化也就知道了。
湍流模拟采用k-ωSST 湍流模型。
1.2 敏感导数解算方法
敏感导数是指优化目标对设计参数的导数,可用于指导设计参数往哪个方向调整,以获得更好的结果。本文采用基于敏感导数的寻优算法,因此如何快速准确地获得敏感导数,成为本研究的关键所在。
最直接的敏感导数计算方法是有限差分法,可以分为单边差分和中心差分两种方式,单边差分格式具有一阶精度,中心差分格式具有二阶精度。有限差分法简单,但是计算量太大,如果有n个设计参数,采用单边差分格式需要进行n+1次数值计算,中心差分格式需要进行2n次数值计算,才能得到全部敏感导数,如果有1000个设计参数,那么优化的第一步就至少需要进行1001次数值计算,因此这种方法只是在设计参数很少时才能应用。
伴随算子敏感导数求解方法可以一次性求出所有敏感导数,计算精度高,计算时间随着设计参数的增加不会明显增多。该方法是通过求解伴随方程,获得伴随算子,然后求得网格参数对设计参数的导数,目标函数对设计参数的偏导数、目标函数对网格的偏导数和流场残差对设计参数的偏导数等,再使用这些计算结果进行一些代数运算获得敏感导数。这种算法的好处在于可一次性获得所有的敏感导数,而且精度很高,有效避免了有限差分法的缺点。由于伴随算子只有在气动布局外形改变之后才需要重新计算,所以每一个优化步,只需要求解一次伴随方程、一次NS方程,使得计算效率大大提高,对于优化变量特别多的优化问题尤其有效,比如对于设计参数为1000的优化计算,只需要进行一次N-S方程求解,一次伴随方程求解,伴随方程求解的复杂程度和耗时与N-S方程基本类似,然后再进行一些代数计算,就可以获得全部的敏感导数。
基于粘性方程的敏感导数计算公式推导如下。
目标函数可以表示为:
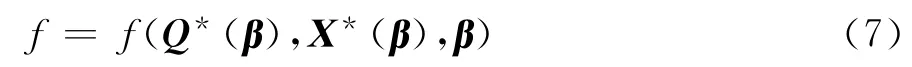
其中各项意义如下:f=f(Q*(β),X*(β),β)为流场变量,上标*表示为收敛的流场变量;X为网格变量组成的矢量;β为设计变量矢量。
上式的差分表达形式为:
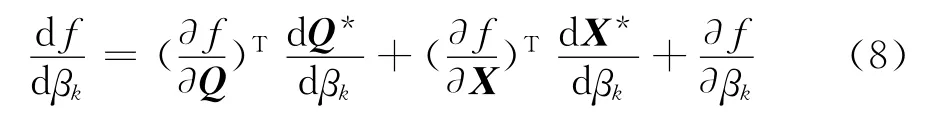
采用伴随方程求解时,加入伴随向量λ,表达式变为:
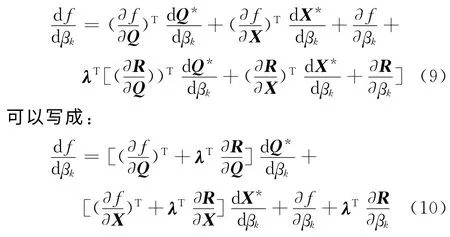
为了避免求解dQ*/dβk时需要多次求解流场,我们令:
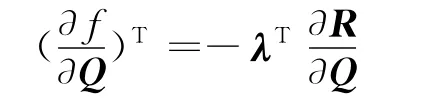
所以在λ求解得到伴随矢量以后,敏感性导数可以由以下公式计算得到:
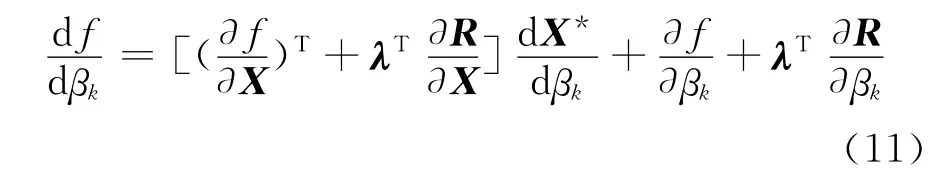
伴随方程的求解分为连续法和离散法,两种方法的结果一致,本项研究中伴随方法的求解采用离散法。首先需要求解伴随方程,求得伴随向量λ以后可以计算敏感导数。
2 参数化外形设计及网格变形方法
本文采用了Bezier-Bernstein外形参数化方法。该方法的优点是能够以比较少的参数,比较精确地表示布局外形,同时又能够对外形进行有效、精确而又细致地调整,还能保持布局表面的光滑性。这一点对于大型飞机气动布局的参数化具有特别重要的意义。主要设计思想是将在每条Bezier-Bernstein曲线上设置几个到几十个控制点,这些点的位置(坐标)就成为设计参数。曲线的数量和每条曲线点的数量取决于布局外形曲面的复杂程度以及优化所要求的精细程度,一般光滑的表面外形,设置十几个控制点就够了。
对于二维的曲线,Bezier可以采用下式表示:
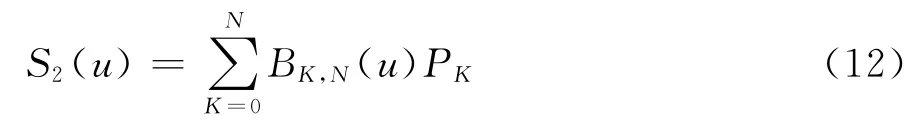
其中,S2(u)=x(u)/y(u),PK=Px/Py是Bezier曲线的控制点,Bernstein多项式BK,N(u)=uK(1-u)N-KN!/[K!(N-K)!]中,u表示曲线的参考弧长,N表示控制点个数,也就数参数数量,Px、Py表示控制点的纵横向坐标。以机翼为例,由于机翼通常在优化过程中,只需要改变控制点的Y坐标,因此设计变量是控制点的Y坐标Py。
由于优化设计中超临界翼型的外形变化不会太大,而且本研究主要采用结构网格,因此采用代数法进行网格变形设计。代数法网格变形技术能够基本满足优化的需求,而且能够比较方便地计算网格点对设计变量的导数,这些导数在使用伴随算子计算敏感导数时需要用到。该方法先移动布局表面的网格点到新位置,然后将这个变动逐渐传递到外围,在传递过程中,根据点的位置按比例调整节点位移量以保证计算域的外边界保持不变。这样还可以保证网格的拓扑结构和附面层网格等非常相似,从而抑制网格变化产生的数值误差,提高优化结果的精度。
3 寻优算法
采用了二次规划寻优算法。优化问题可以描述为:
最小化目标函数:F(β);约束条件:gi(β)≤0,i=1,l;hj(β)=0,j=1,m;βlk≤βk≤βnk,k=1,NDV。其中,β=(β1,β2,β3,β4……)T表示设计变量。在求解过程中,二次规划寻优算法通过目标函数值及其敏感导数,用二次曲面在优化起始点附近拟合目标函数。给出能使得目标函数最优的设计参数变化方向和大小。计算获得新的目标函数值,并判断新的设计点是否满足约束条件,是否优于老的设计点。重复这个循环,直到满足优化收敛条件。这种寻优算法只能得到局部最优点,本文针对大飞机机翼的特点,对这种算法进行了一些改进,提高了优化效果。
4 W9大飞机布局的多参数优化设计
4.1 基本外形气动特性
W9布局基本外形如图1所示,机翼表面的压力分布如图2所示。
原始外形全机巡航升力系数CL=0.5,升阻比K=17.53,阻力系数CD=0.02853。
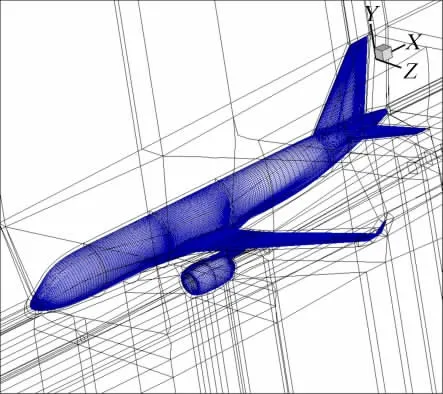
图1 W9布局外形及表面网格分布Fig.1 The original shape and surface grids of the W9
4.2 设计条件
以给定的初始大型飞机布局为基础,在全机状态下对机翼进行多参数的减阻优化,这样所得到的优化结果就计入了短舱、机身、挂架等部件对机翼的影响。机翼初始外形及网格如图1。设计目标与设计要求如下:
设计要求:CL≥0.5,Ma=0.785,Re=2.4×107,保持机翼最大相对厚度不减小;设计目标:减阻;
设计参数:设计参数168个,短舱挂架左右的机翼各使用5 个截面控制,每个截面上下表面各8 个Bezier控制参数,前后缘点不动,短舱上方使用8个设计参数控制,总计168个设计参数,控制面位置及原形压力分布见图2。
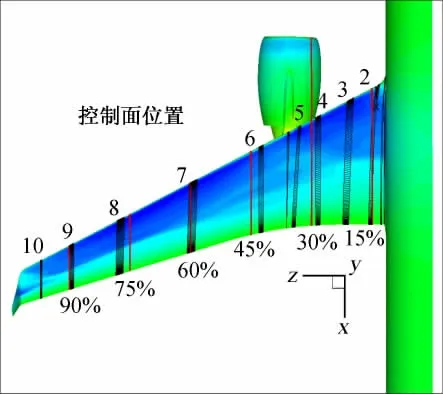
图2 机翼展向控制面的位置Fig.2 The position distribution of wing span control section
4.3 优化结果与分析
优化前:CL=0.5,CD=0.02853,K=17.53;优化后:CL=0.5,CD=0.02785,K=17.95。优化总共进行了41步,阻力变化过程如图3所示。
整个优化设计共计进行了41步,最大的一步阻力减小也不到2个阻力单位,其中很多优化步的阻力减小量小于0.2个阻力单位。那么,这么小的阻力优化量,其计算结果是否可靠呢?优化过程本身就能说明这个问题,虽然每一步的优化量不大,但是整个优化过程进行的很顺利,每一步都较前一步阻力有所减小,虽然有些优化步的减小量很小。如果这些阻力的变化仅仅是数值误差的话,那么受到数值误差干扰的优化过程就无法顺利的进行下去,中间必然会出现阻力增大的情况。由于网格的数量和质量较高,同时阻力收敛较好,优化过程中又保证了网格的相似性,因此阻力变化量的计算精度很高,能够满足大型飞机精细优化设计的计算精度要求。
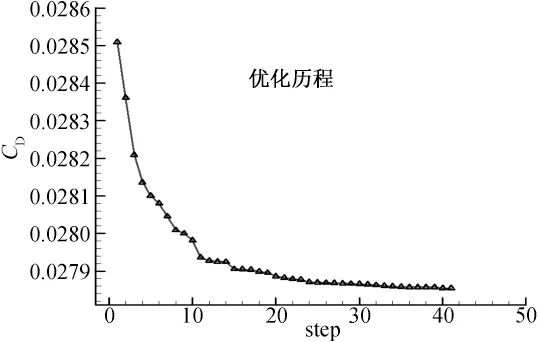
图3 优化过程中阻力的变化Fig.3 Variation of drag coefficient with the optimization process
相比优化前,阻力减小了6.8个阻力单位,占全机总阻力的2.38%。这个比重虽然比较小,但是考虑到这种优化只能减小机翼的压差阻力,并不能减小摩擦阻力,而机翼的总阻力为0.0144,因此阻力减小量约为机翼阻力的4.72%,占压差阻力的比重就更大,接近10%。为了验证优化结果的可靠性,采用了相同的网格和湍流模型,使用空气动力学国家重点实验室的亚跨超平台Trip 2.0进行了验算。验算得到的升力值和阻力值均与原值有一定的差别,阻力系数相差约4个阻力单位,但是阻力优化量却变化很小,验算得到的阻力优化量约为6.6个阻力单位,减小了约0.2个阻力单位。从验算结果可以看出,本次优化的精度是很高的,结果是可信的。
图4给出了优化前后机翼的表面压力分布对比,从图中可以看出,优化后机翼上表面的激波明显减弱,消除了原型机翼上外翼部位存在的二次压缩与膨胀。图5到图8给出了机翼展向30%到60%共计2个截面的压力分布和形状对比图。从图中可以看出,优化后的机翼压力分布更加接近标准的超临界压力分布,激波更弱,部分截面激波消除。原形压力分布中的凹坑被抹平。下表面压力分布基本未变,整个机翼的截面外形改变较小,截面最大厚度基本保持不变。其他截面的压力分布变化与这两个截面类似,由于篇幅所限,不再一一列出。
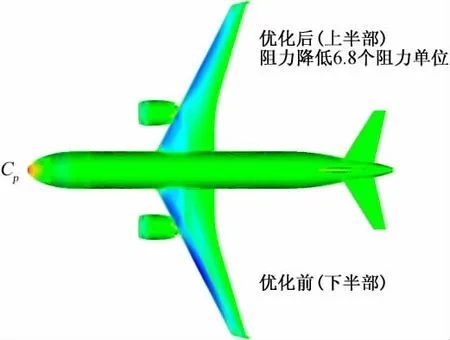
图4 优化前后压力分布对比图(168设计变量)Fig.4 The comparison of surface pressure distribution of original shape and optimized one(168design variables)
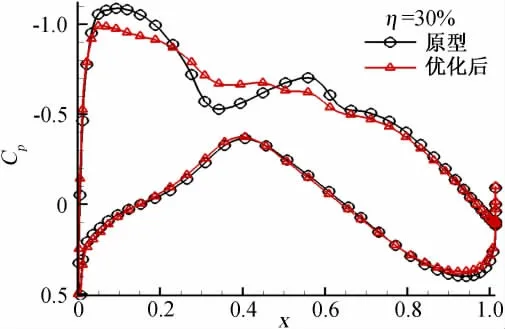
图5 机翼展向30%截面处优化前后压力分布对比Fig.5 Pressure distribution comparison between original and optimized at 30% wing span section for W9
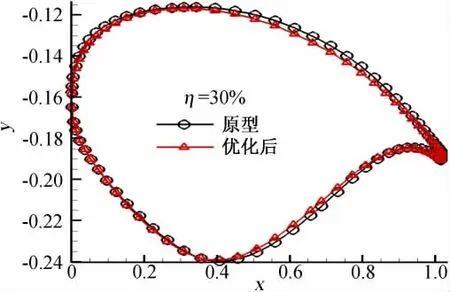
图6 机翼展向30%处翼型优化前后外形对比图Fig.6 The comparison of airfoil shape of original and optimized at 30% wing span section for W9
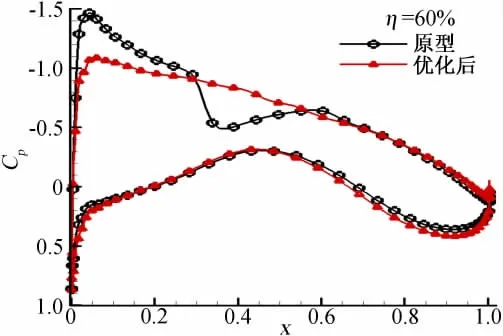
图7 机翼展向60%截面处优化前后压力分布对比Fig.7 Pressure distribution comparison between original and optimized at 60% wing span section for W9
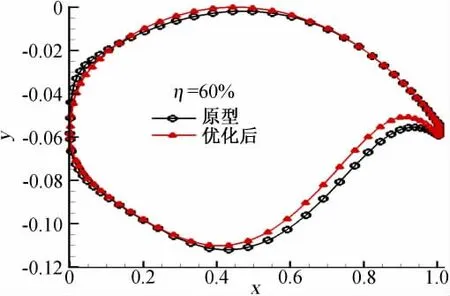
图8 机翼展向60%处翼型优化前后外形对比图Fig.8 The comparison of airfoil shape of original and optimized at 60% wing span section for W9
5 结论
从优化结果可以看出本文采用的优化方法是有效的,所采用的数值方法、伴随算子解算方法、寻优方法能够满足大型飞机全机构型多参数高精度优化设计的要求,优化结果与理论分析相符。虽然原始外形已经经过常规设计手段的多轮优化,其性能已经很高,但是多参数精细优化仍然取得了明显的优化效果,在保持升力不变,最大厚度不减小的前提下阻力降低了0.00068,减小了2.38%,其中机翼阻力减小了4.72%。从截面压力分布来看,优化后的截面压力分布明显改善。这与总阻力的减小能够互相印证。
从优化过程和验证结果来看,本次优化设计对阻力变化量的计算精度较高,能够满足大飞机气动布局优化精细设计的要求。
[1]IRONNEAU O.On optimum design in fluid mechanics[J].JournalofFluidMechanics,1974,64(1):97-110.
[2]JAMESON A.Aerodynamic design via control theory[J].JournalofScientificComputing,1989,3(3):233-260.
[3]JAMESON A.Optimum aerodynamic design using CFD and control theory[R].AIAA 95-1729,1995.
[4]JAMESON A.Automatic design of transonic airfoils to reduce the shock induced pressure drag[A]//Proceedings of the 31st Israel Annual Confer-ence on Aviation and Aeronautics[C].Tel.Aviv.,1990.
[5]MOIGNE A L,QIN N.Variable-fidelity aerodynamic optimization for turbulent flows using a discrete adjoint formulation[J].AIAAJournal,2004,42(7):1281-1292.
[6]QIN N,WONG W S,MOIGNE A L.Three-dimensional contour bumps for transonic wing drag reduction[J].ProceedingsoftheInstitutionofMechanicalEngineers,PartG:JournalofAerospaceEngineering,2008,222(5):619-629.
[7]MOIGNE A L.A discrete Navier-Stokes adjoint method for aerodynamic optimization of blended wing-body configurations[D].[PhD Thesis].Cranfield,Cranfield University,2002.
[8]GILES M B,PIERCE N A.An introduction to the adjoint approach to design[J].Flow,Turbulenceand Combustion,2000,65(3):393-415.
[9]黄勇,陈作斌,刘刚.基于伴随方程的翼型数值优化设计方法研究[J].空气动力学学报,1999,17(4):413-422.
[10]周铸,陈作斌.基于N-S方程的翼型气动优化设计方法研究[J].空气动力学学报,2002,20(2):141-149.
[11]唐智礼,黄明恪.基于控制理论的Euler方程翼型减阻优化设计[J].空气动力学学报,2001,19(3):262-270.
[12]唐智礼,黄明恪.约束最优控制理论及其在气动优化中的应用[J].力学学报,2007,39(2):273-277.
[13]乔志德,杨旭东,朱兵.亚、跨音速三维机翼气动外形反设计的控制理论方法[J].2003,21(1):11-19.
[14]杨旭东,乔志德.基于共轭方程法的跨音速机翼气动力优化设计[J].航空学报,2003,24(1):1-5.
[15]李少峰,乔志德,杨旭东.基于控制理论方法的翼型最大升力优化设计[J].航空计算技术,2005,35(4):98-102.
[16]杨旭东,乔志德,朱兵.基于控制理论和NS 方程的气动优化设计方法研究[J].空气动力学学报,2005,23(1):46-51.

