雷诺数对飞机气动特性的影响研究
张培红,周乃春,邓有奇,马明生
(中国空气动力研究与发展中心计算空气动力研究所,四川 绵阳 621000)
0 引言
由于风洞尺寸和试验条件的限制,风洞试验雷诺数一般比飞行雷诺数要低1~2个量级,这就导致风洞测量得到的飞机气动特性与实际飞行条件下的气动特性存在一定的差别。对于飞机设计人员来说,一直都存在着如何把风洞试验数据外推到真实条件下飞行数据的问题,也就是通常所说的雷诺数修正问题[1]。
雷诺数不同,通常会对边界层的类型、转捩点的位置、边界层内速度分布形态、物体上分离点的位置、分离形态和分离区大小,以及激波位置、边界层的厚度等产生影响,从而导致飞机气动特性的变化。
长期以来,经过不断探索和总结,在飞机设计过程中,通常认为雷诺数对升力和俯仰力矩随攻角变化曲线的斜率影响不大,仅需对风洞试验数据的阻力系数和最大升力系数进行修正[1],这样的处理方法对于战斗机来说是适用的[2,5],不会产生很大的误差。随着对雷诺数影响认识的不断提高,人们发现[3],对于具有中等厚度或大厚度机翼的运输类飞机,这样的处理就会产生较大的误差。相关研究[1,4]表明对于中等或大厚度的机翼以及后体收缩的机身,雷诺数影响规律与过去小展弦比机翼和后体不收缩机身的影响规律完全不同,雷诺数不仅仅影响阻力和最大升力系数,而且影响升力和俯仰力矩随攻角变化曲线的斜率。
本文通过对某翼身组合体和某战斗机不同雷诺数下的气动特性进行研究,分析了运输类飞机和战斗机类飞机气动特性的雷诺数影响规律。并试图通过分析不同翼型气动特性的雷诺数影响,解释雷诺数对运输类飞机和战斗机气动特性影响强弱不同的原因,从而探讨雷诺数对飞行器气动特性产生影响的一些关键参数,进而促进雷诺数影响的相关性分析工作。
1 数值方法
本文采用中国空气动力研究与发展中心计算空气动力研究所研制的亚跨超声速流场解算器MFlow。MFlow 解算器是基于求解格心的非结构混合网格和雷诺平均Navier-Stokes方程的大规模并行解算器。它可以使用任意形状的网格单元,具有较大的灵活性,目前使用最多的主要有四面体、三棱柱、金字塔和六面体。采用有限体积法对空间进行离散,未知变量位于网格单元的体心。离散方程组的求解采用隐式LU-SGS 方法或显式Runge-Kutta方法,采用FAS融合多重网格方法加速收敛。MFlow 解算器有各种不同的选项可以使用,例如各种空间对流项和扩散项离散格式、各种时间迭代方法、不同的湍流模型等等。
计算时采用有限体积法,空间项离散采用Roe通量差分裂方法,采用隐式LU-SGS 时间项离散方法求解[8]。湍流模型采用S-A 一方程湍流模型。
1.1 控制方程
守恒形式的非定常可压缩N-S方程[6]:
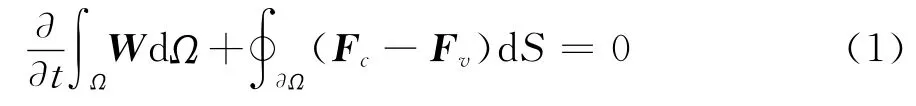
其中,Ω表示控制体的体积,∂Ω表示控制体封闭面的面积,W为守恒变量,Fc为无粘通量,Fv为粘性通量。
1.2 边界条件
任何数值模拟都只能考虑真实物理区域的一部分,物理区域的截断产生一个人工边界,在边界上必须指定某些物理量的值。此外,与流体接触的固壁代表物理区域的自然边界。边界条件的处理必须特别注意,不合适的边界条件会引起对真实系统的不正确模拟,而且对解的收敛速度和稳定性也有很大影响。本文中用到的边界条件主要有:
(1)远场边界条件:采用基于局部一维Riemann不变量的无反射边界条件;
(2)无滑移物面边界条件:无滑移、绝热。
1.3 S-A湍流模型
S-A 一方程模型是从经验和量纲分析的角度出发,在简单流动的基础上经过逐步补充而发展到适用于有层流流动的固壁湍流流动的一方程模型[2]。
积分形式的S-A 模型方程为:
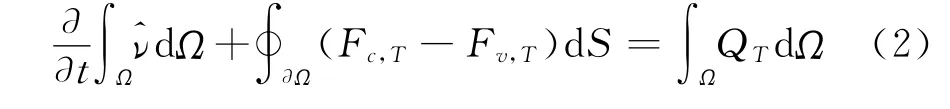
其中Ω表示控制体,∂Ω是控制体的面,dS是控制体的面元。
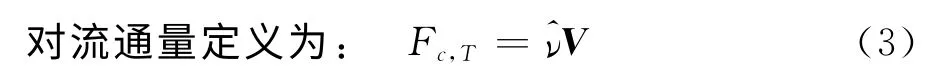
其中V表示逆变速度:
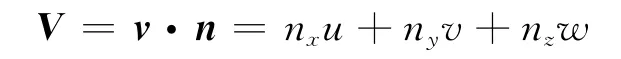
源项定义为:
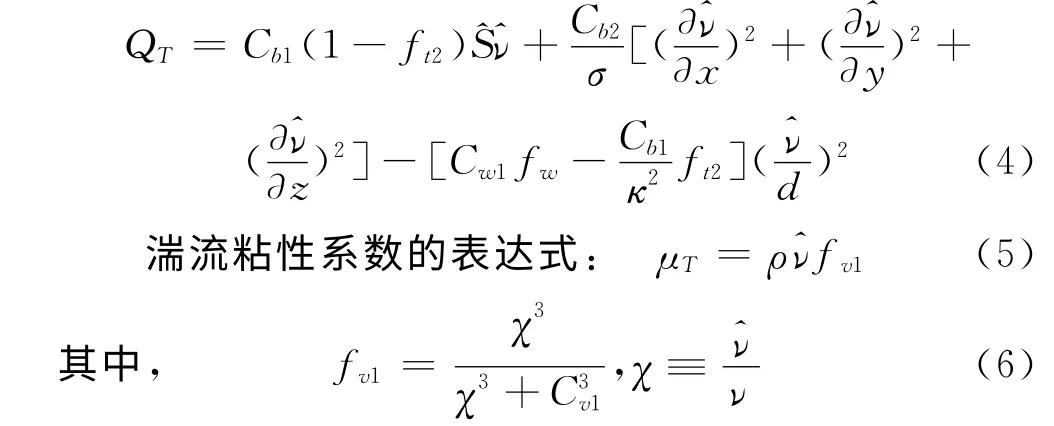
上式中各参数可由下列公式求得:
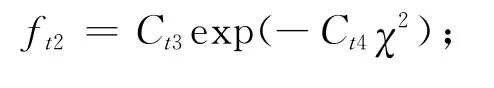
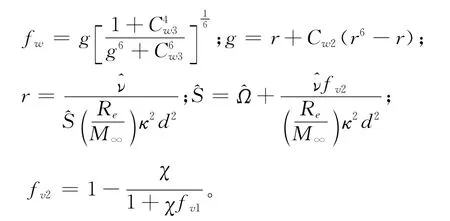
d控制体体心到物面的距离;
模型常数为:
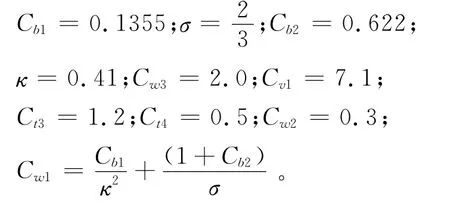
2 算例验证
为了对MFlow 解算器进行考核和验证,我们首先对DLR-F4标模进行了计算,并与试验值和第一届阻力会议提供的不同程序计算结果进行了比较。
计算条件:M=0.75;α=-3°,-2°,-1°,0°,1°,2°;温度T=283.15K;雷诺数Re=3.0×106(基于平均气动弦长Cref=0.1412m)。
图1 是F4 的计算网格示意图。网格单元总数为2164万个。其中四面体单元1368万个,三棱柱单元795万个。物面单元数为29.5万个,物面法向三棱柱网格数为27个,物面法向第一层间距约为1.0×10-6m。
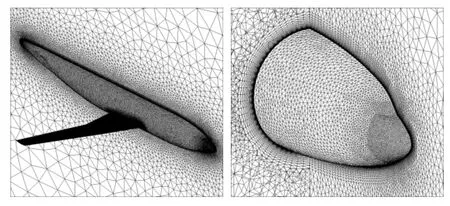
图1 DLR-F4网格Fig.1 Grid of DLR-F4
图2给出了本文计算得到的极曲线和试验结果以及Tau、NSU3D、USM3Dns等不同软件计算得到的结果比较。可以看出,三个风洞试验结果具有很好的一致性,本文计算结果落在其它几个程序计算结果之间,与试验结果吻合较好。
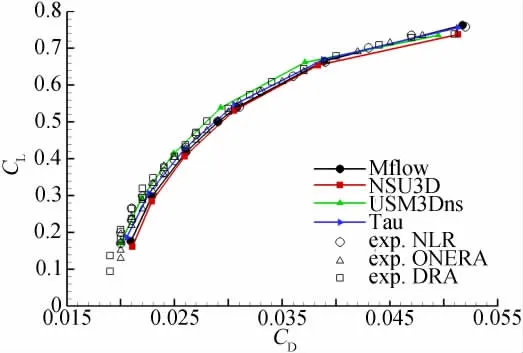
图2 DLR-F4极曲线Fig.2 Polor curve of DLR-F4
图3 给出了F4的机翼典型剖面压力分布比较。几个程序的计算结果都非常接近,与试验结果符合得也较好,只是所有计算结果的前缘吸力峰值都要比试验值低,激波位置靠前,波后压力系数偏大。几个计算结果相比,差别主要体现在激波位置。
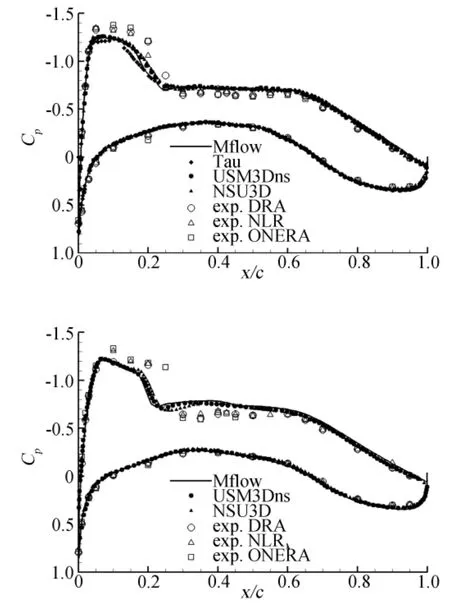
图3 DLR-F4压力分布Fig.3 Pressure distribution of DLR-F4
图4给出了机翼表面流线和翼根处分离气泡的细节。可以看出计算得到的流场结构清晰,机翼沿展向后缘有明显的分离线,翼身结合处后缘有较大的分离气泡。
通过以上计算和分析,可以看出MFlow 解算器可以较好地模拟飞机的气动特性和流场结构,具有较强的可靠性和鲁棒性。
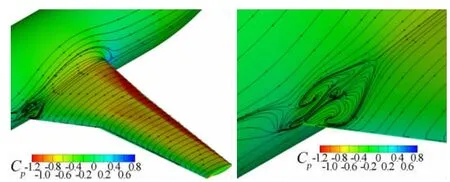
图4 DLR-F4表面流线Fig.4 Streamline of DLR-F4
3 结果分析与讨论
为了分析雷诺数对战斗机外形气动特性的影响规律,采用MFlow 解算器对某战斗机外形在不同雷诺数下的气动特性进行了模拟。图5、图6 为M=0.6时不同雷诺数下升力曲线和极曲线。图7、图8为M=2.0时不同雷诺数下升力曲线和极曲线。
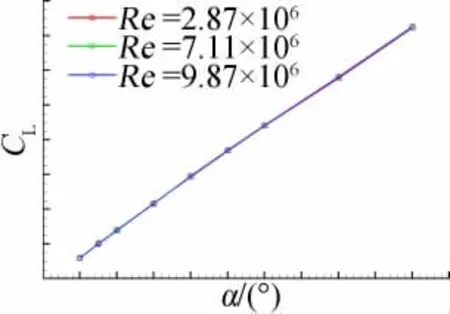
图5 不同雷诺数下的升力比较曲线(M=0.6)Fig.5 Comparision of lift coefficients for different Re
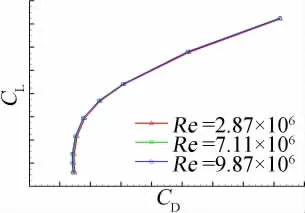
图6 不同雷诺数下的极曲线(M=0.6)Fig.6 Comparision of polars for different Re
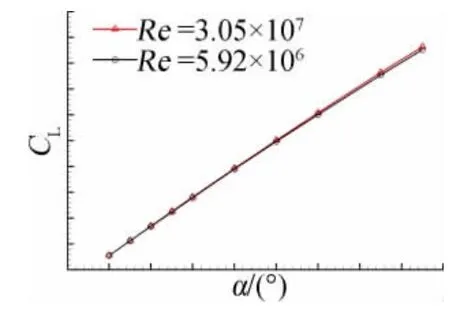
图7 不同雷诺数下的升力比较曲线(M=2.0)Fig.7 Comparision of lift coefficients for different Re
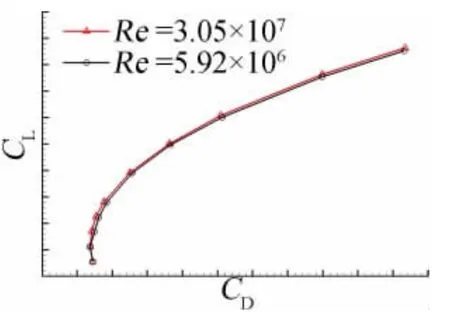
图8 不同雷诺数下的极曲线(M=2.0)Fig.8 Comparision of polars for different Re
可以看出,雷诺数增加,升力系数和升力线斜率增大,阻力系数和最小阻力减小。但雷诺数对升力系数和升力线斜率的影响相对很小,在工程实际中可以不考虑。相关研究表明,雷诺数主要是影响战斗机的最大升力系数和阻力,所以在战斗机的设计中,通常直接使用风洞测量得到的升力,而不用进行修正,只对阻力和最大升力进行修正。
为分析雷诺数对运输类飞机气动特性的影响规律,我们采用MFlow 解算器对某翼身组合体带吊舱外形在不同雷诺数下的气动特性进行了模拟。图9给出了翼身组合体外形示意图。

图9 翼身组合体外形Fig.9 Figuration of wing-body
图10、图11给出了M=0.15时不同雷诺数下升力曲线和极曲线。图12、图13给出了M=0.77时不同雷诺数下升力曲线和极曲线。可以看出,雷诺数对运输类飞机气动特性的影响要比对战斗机气动特性的影响复杂的多,特别是对升力系数和升力线斜率的影响显著增大,因此在运输类飞机设计时,试验得到的升力、阻力数据都必须经过修正才能使用。雷诺数对运输类飞机气动特性的影响规律与对战斗机类飞机气动特性的影响规律基本相同,随雷诺数增加,升力系数和升力线斜率增大,阻力系数和最小阻力减小,升力随攻角变化线性范围增加,飞机升阻特性明显改善。
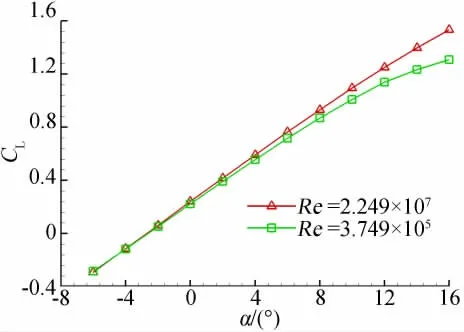
图10 不同雷诺数下的升力比较曲线(M=0.15)Fig.10 Comparision of lift coefficients for different Re
为分析雷诺数对运输类飞机和战斗机类飞机产生不同影响规律的原因,并进一步探讨雷诺数对飞行器气动特性产生影响的一些关键参数,我们对五个不同翼型的气动特性进行了雷诺数影响计算。
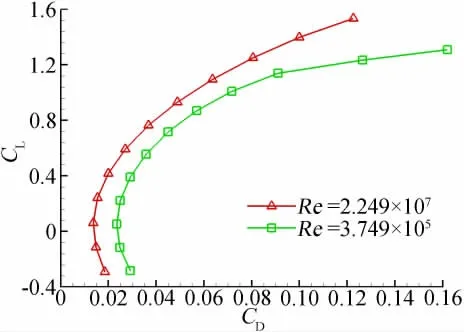
图11 不同雷诺数下的极曲线(M=0.15)Fig.11 Comparision of polars for different Re
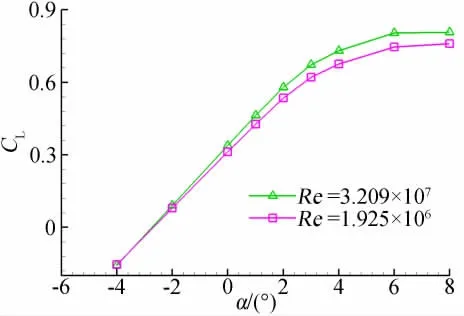
图12 不同雷诺数下的升力比较曲线(M=0.77)Fig.12 Comparision of lift coefficients for different Re
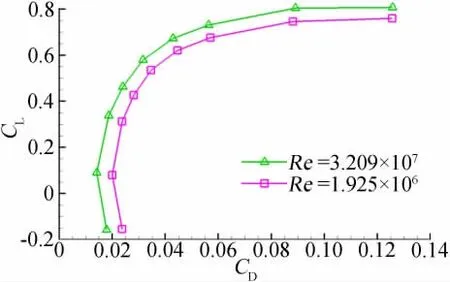
图13 不同雷诺数下的极曲线(M=0.77)Fig.13 Comparision of polars for different Re
五个翼型分别为超临界翼型SC(2)0010,即10%厚度的对称翼型;与SC(2)0010具有相同厚度分布、且设计升力系数为1.0 的超临界大弯度翼型SC(2)1010;相对厚度为4%的对称翼型NACA0004;相对厚度为4%,设计升力系数0.4的NASA超临界翼型SC(2)0404;相对厚度6%,设计升力系数为1.0 的NASASC(2)1006 超临界翼型。翼型剖面示意图如图14。计算条件:马赫数为0.4、0.75,单位雷诺数分别为:2.59×106和1.55×105,力矩参考点在1/4弦线点。

图14 翼型剖面示意图Fig.14 Sketch map of airfoil profiles
图15、图16给出了马赫数0.4时,雷诺数对不同翼型升力系数、俯仰力矩系数影响曲线。可以看出对于相对厚度10%的对称翼型SC(2)0010,雷诺数变化对升力和俯仰影响都很小。对于相对厚度10%,设计升力系数为1.0 的大弯度翼型SC(2)1010,雷诺数变化对升力和俯仰力矩影响非常明显;雷诺数增加,升力增大,升力线斜率增加,同时产生一个低头力矩增量。图17、图18给出了马赫数0.75时的计算结果,雷诺数影响规律与马赫数0.4时相同。
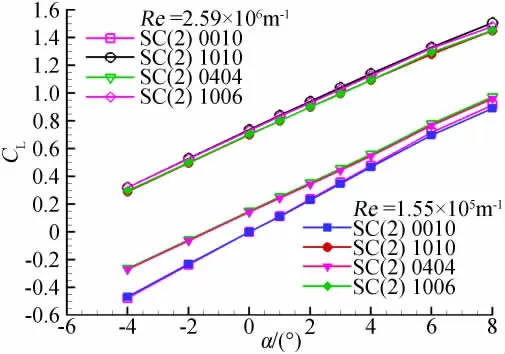
图15 雷诺数对不同翼型升力系数影响Fig.15 Re effect on lift coefficients for different airfoils

图16 雷诺数对不同翼型俯仰力矩系数影响Fig.16 Re effect on pitching moment coefficients for different airfoils
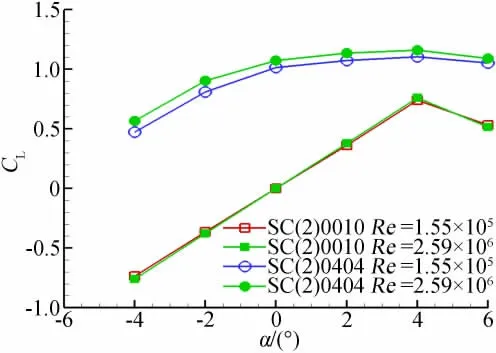
图17 雷诺数对不同翼型升力系数影响(M=0.75)Fig.17 Re effect on lift coefficients for different airfoils
对于相对厚度4%的有弯度翼型SC(2)0404,和相对厚度6%的有弯度翼型NASASC(2)1006,雷诺数变化对升力和俯仰力矩的影响规律和对SC(2)1010翼型的相同,但影响相对要小。说明厚度小的翼型,雷诺数影响相对就小。
图19给出了雷诺数变化引起的SC(2)1010和SC(2)1006升力增量和俯仰力矩增量。可以看出,雷诺数对SC(2)1010 升力和俯仰力矩的影响要比对SC(2)1006升力和俯仰力矩的影响大。说明对于相同厚度的翼型,弯度越大,雷诺数的影响就越大。
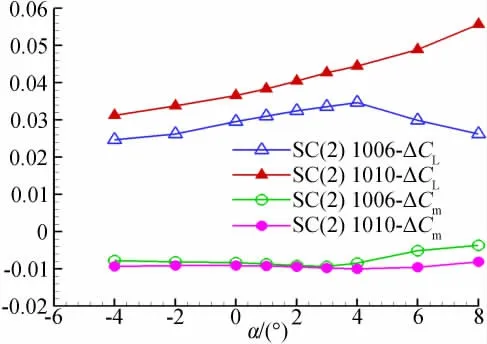
图19 雷诺数变化引起的SC1006与SC1010升力和俯仰力矩增量Fig.19 Increment of lift and pitching moment coefficients by different Re
以上分析说明,雷诺数对气动特性的影响与外形相关,雷诺数对对称翼型升力和俯仰力矩的影响很小,翼型的厚度和弯度越大,雷诺数对其气动特性的影响越明显。
通过分析雷诺数对翼型气动特性的影响规律,以及影响雷诺数影响强弱的关键参数,我们可以进一步探讨雷诺数对战斗机和运输机影响强弱不同的原因。对于战斗机来说,机翼多为尖前缘的薄机翼,相对厚度较小,且一般具有很小的弯度;而对于运输类飞机,一般具有钝前缘,相对厚度大,且一般具有很大的弯度。而机翼又是决定飞机气动特性的关键部件,这就使得雷诺数的变化,对运输类飞机气动特性的影响远远比对战斗机气动特性的影响复杂。
4 结论
本文采用MFlow 软件对战斗机和运输类飞机气动特性的雷诺数影响规律进行了分析,并通过研究不同翼型气动特性的雷诺数影响,探讨了雷诺数对战斗机和运输类飞机影响强弱不同的原因,并得到了雷诺数对飞机气动特性影响的关键参数。可以得到以下结论:
(1)雷诺数对气动特性影响与外形相关。
(2)翼型厚度减小,弯度减小,雷诺数对翼型气动特性的影响减小。
(3)雷诺数对运输类飞机气动特性的影响比对战斗机气动特性的影响复杂的多。
[1]HAINES A B,YOUNG A D.Scale effects on aircraft and weapon aerodynamics[R].AGARD-AG-323,1994.
[2]朱自强,吴宗成.现代飞机设计空气动力学[M].北京航空航天大学出版社,2005.
[3]JOHNSON F T,TINOCO T,JONG Y N.Thirty yearsof development and application of CFD at Boeing commerical airplane seattle[R].AIAA 2003-3439.
[4]LITTLE B H,etc.High Reynolds number subsonic aerodynamics[R].AGARD-LS-37-70,1970.
[5]WENDY B L.Subsonic analysis of 0.04-scale F-16XL models using an unstructured Euler code[R].NASA T P 3597,1996.
[6]曾扬兵,沈孟育.N-S方程在非结构网格下的求解[J].力学学报,1996,28(6):641-649.
[7]FISHER D F,etc.Reynolds number effects at high angles of attack[R].NASA TP-1998-20655.
[8]HASELBACHER A,BLAZEK J.On the accurate and efficient discretisation of the Navier-Stokes equations on mixed grids[R].AIAA 99-3363,1999.

