中等后掠角三角翼前缘双涡结构的形成机理数值研究

刘 杰，刘沛清，闫指江

（1.北京航空航天大学流体力学教育部重点实验室，北京 100191；2.成都飞机设计研究所，四川 成都 610091）

0 引言

在飞机布局中，三角翼布局是一种非常重要的布局。三角翼飞行器机动、灵活、结构简单，具有体积小、重量轻、安全可靠等特点，它已经被许多研究［1－2］证实能够实现大迎角、超机动飞行和具有良好的过失速机动性能。三角翼上的流场十分复杂且具有强烈的旋涡流动的特性。现在许多研究［3－5］都发现对于中小后掠角三角翼，在特定的雷诺数和迎角下，在机翼前缘涡主涡外侧会形成一个新的集中涡，即形成双涡结构：鲁素芬［3］对50°后掠角三角翼流动结构及气动特性的实验研究发现了三角翼前缘双涡结构的存在；GURSUL I［4］通过数值研究发现小后掠角的三角翼容易形成双涡结构，而细长三角翼不会产生双涡结构，其认为双涡结构产生的原因是边界层和主涡之间的相互作用；GORDNIER Raymond E 和VISBAL Miguel R［5］对50°后掠角平板三角翼在迎角等于5°时的流动进行了数值模拟，结果表明在一定的雷诺数下，由于粘性作用的减弱，二次涡将一次涡分成了两个独立的集中涡，从而导致了双涡结构的形成。虽然现在许多研究都发现了机翼前缘双涡结构，但是双涡结构的机理目前尚无定论。因此本文利用数值计算的方法，对机翼前缘后掠角为50°的中等后掠角三角翼布局的流场进行了分析研究，以揭示50°三角翼前缘双涡结构形成演变机理。

1 计算与实验方法

1.1 计算模型及计算方法

计算模型选用的是简化的三角翼布局。模型边缘均迎风面倒角45°。图1给出了三角翼物理模型平面示意图。机翼的前缘后掠角Λ为50°，根弦长为c＝0.2586m，机翼展长L＝0.434m，机翼面积S＝0.05625m2，模型厚度为4mm。

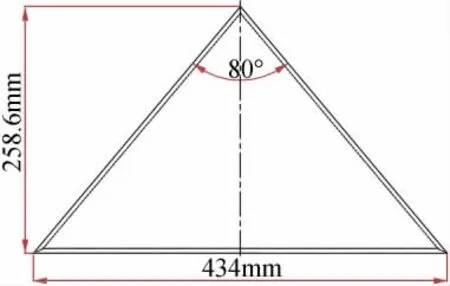
图1 模型平面示意图Fig.1 Schematic diagram of the model

数值计算采用的基本方程为不可压缩流动Reynolds平均Navier－stokes方程：

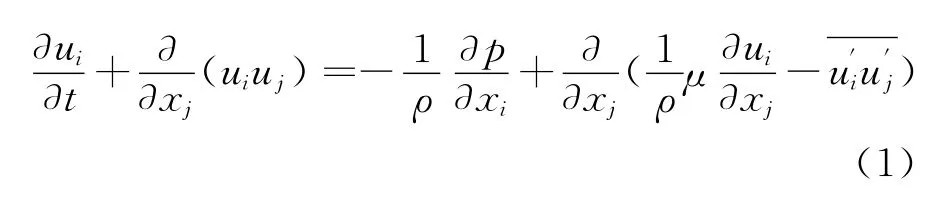
湍流模型采用SSTk－ω模型。SSTk－ω模型考虑了低雷诺数和剪切流，同时加入了横向耗散导数项，在湍流粘度的定义中考虑了湍流剪切应力的输运过程，适于进行带逆压梯度的流动计算、翼型计算等。

由于在机翼前缘附近存在前缘涡、二次分离等复杂的流动分离现象，因此对该区域的网格进行了加密；在流场空间，由于模型近壁面的速度梯度比较大，所以在模型近壁面附近对网格进行了加密。图2给出了三角翼模型计算网格示意图。

图2 模型计算网格Fig.2 Computation grid for the delta wing

计算设定的自由来流速度为20m／s，基于机翼根弦长的雷诺数为2.4×105。压力与速度耦合方式采用SIMPLEC算法，对流项离散格式采用二阶迎风格式，模型表面采用固壁边界条件。

1.2 计算结果与风洞实验结果的比较

为了验证数值计算结果的准确性，将计算结果与风洞测力测压实验结果进行了对比分析。所用的验证实验数据均来自温瑞英的博士论文［6］，测力和测压实验是在北京航空航天大学的D4 低速风洞中完成的。图3给出了50°三角翼升力系数随迎角变化特性的对比曲线，图4给出了迎角等于16°时机翼上表面压力分布的对比曲线。可以看到，在失速迎角以前，计算值和实验值相符得很好，而当迎角进一步增大时，计算结果较实验值偏高。

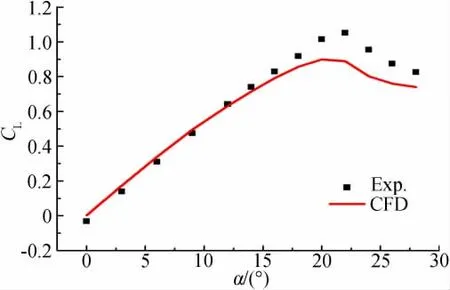
图3 升力系数随迎角变化特性的对比曲线Fig.3 Lift coefficient with the angle of attack

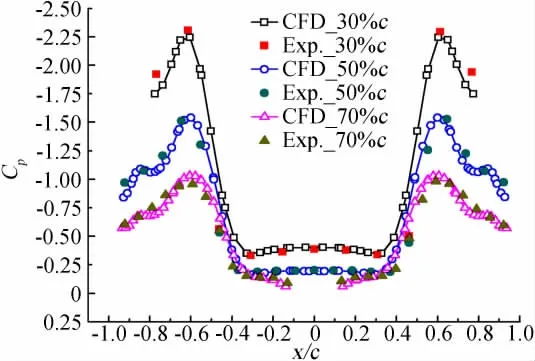
图4 机翼上表面压力分布的对比曲线（α＝16°）Fig.4 Comparison of pressure coefficient distribution on the upper surface of the wing（α＝16°）

2 计算结果

图5是计算得到的在不同迎角时模型20%根弦位置垂直流向截面的轴向涡量分布图，图6是不同迎角时模型空间流线分布情况。我们可以看到在迎角较小时，在机翼上表面只是形成了一个集中涡；而随着迎角的增加，在机翼前缘涡主涡外侧会形成一个新的集中涡，此时翼面上出现了两个集中涡（以后称靠近机翼翼根的集中涡为机翼前缘内涡，称靠近机翼前缘的集中涡为机翼前缘外涡），即出现机翼前缘双涡结构，相比内涡机翼前缘外涡的强度以及影响范围都要小一些；迎角进一步增大，前缘内涡的强度以及影响范围变得越来越大，外涡逐渐被“挤”到更加靠近外侧的位置逐渐向机翼前缘靠近，前缘附近三维分离产生的自由剪切层更多的被卷入内涡；最后当迎角达到20°时外涡消失，此时翼面上只剩下一个集中涡，双涡结构消失。图7为迎角等于12°的情况下垂直流向截面的激光片光实验结果［6］，我们能观察到此时在机翼翼面上出现了双涡结构。

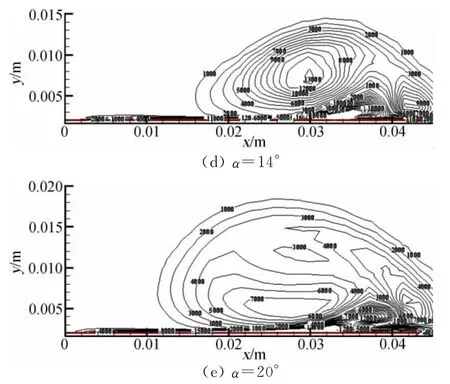
图5 不同迎角时垂直流向截面的轴向涡量分布图（x／c＝20%）Fig.5 The axial vorticity distribution at different angles of attack（x／c＝20%）

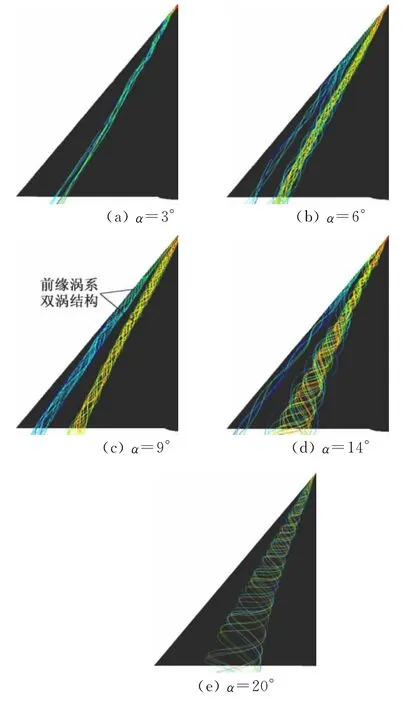
图6 不同迎角时模型空间流线分布情况Fig.6 Streamlines off the leading－edge of this wing at different angles of attack

图7 垂直流向截面的激光片光实验结果［6］（α＝12°）Fig.7 Results of the laser light sheet experiment over the delta wing along the measuring plane atα＝12°［6］

3 中等后掠角三角翼双涡结构形成机理

对于具有尖前缘的细长三角翼在不大的迎角下，其迎风面上的层流流动已经不能绕过机翼的尖前缘，背风面上的边界层也流向前缘，结果在前缘处会形成自由涡层型三维分离，该自由涡层很薄且在主流中不断卷起，进而在翼面上方形成稳定的螺旋型集中涡，即前缘涡。由目前的研究看来，前缘集中涡的形成条件，一是要在前缘能形成自由涡层型三维分离，二是主流沿涡轴方向应该具有一定大小的速度分量，使自由涡层能沿涡轴方向不断发展、卷起，最后形成集中涡［2］。许多研究表明，三角翼的流场结构与前缘后掠角、雷诺数、来流几何迎角、旋涡的强度、旋涡的轴向速度等有关［6］，即：

其中，Λ为三角翼前缘后掠角，α为来流几何迎角，Re为实验雷诺数，Γ为旋涡的强度，Vz为旋涡的轴向速度，V∞为来流速度，c为模型的根弦长。

图8是来流速度分解示意图。其中

迎角α越大，自由来流速度沿法向（垂直机翼翼面方向）上的速度分量Vζ就越大，这也就促进了机翼前缘处的流动分离，相应地会产生更多的自由剪切层；机翼前缘后掠角Λ越大，主流沿涡轴方向的速度分量Vτ越大，旋涡的轴向速度Vz就也越大，前缘附近流动分离所生成的自由剪切层就更容易发生卷绕形成集中涡。

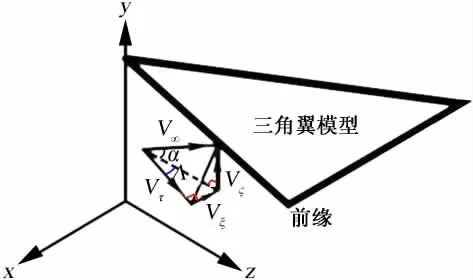
图8 来流速度分解示意图Fig.8 Schematic diagram of flow velocity decomposing

在一定的雷诺数条件下，对于中等后掠角三角翼，迎角较小时，机翼翼面上只会形成一个集中涡，前缘涡单涡结构平面示意图如图9所示。这是因为迎角较小时自由来流速度沿垂直机翼翼面方向上的速度分量Vζ并不是很大，机翼前缘附近流动分离产生的自由剪切层不是很强，那么涡轴方向的速度分量足以使所有在机翼前缘附近产生的自由剪切层发生卷绕而形成一个集中涡，即形成机翼前缘单涡结构；随着迎角的增加，Vζ变大，这就加剧了机翼前缘处的流动分离，相应地也就增强了自由剪切层，此时涡轴方向的速度分量不足以带走所有的自由剪切层，那么剩余的自由剪切层就在前缘主涡的外侧形成了一个新的旋向相同的集中涡，即在机翼翼面上形成前缘双涡结构，双涡结构平面示意图如图10所示；随着迎角的继续增大，前缘附近分离产生的自由剪切层更多地被前缘内涡卷走，内涡的强度以及影响范围越来越大，同时前缘外涡在内涡以及其下二次涡的影响下，逐渐被“挤”到更加靠近外侧的位置，前缘外涡的强度越来越小，当到达某一迎角时，前缘外涡消失，机翼翼面上将不再出现双涡结构。

图9 前缘单涡结构平面示意图Fig.9 Schematic diagram of the single vortex structure

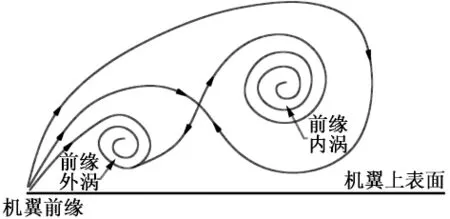
图10 前缘双涡结构平面示意图Fig.10 Schematic diagram of the dual vortex structure

综上可得对于中等后掠角的三角翼，只是在一定的迎角范围内才会形成前缘双涡结构，中等后掠角三角翼前缘双涡结构的形成主要取决于三角翼前缘附近三维分离产生的自由剪切层强度和涡轴方向的速度分量之间的大小关系。当涡轴方向的速度分量足以使前缘附近分离产生的所有自由剪切层卷绕而形成一个集中涡时，此时在机翼翼面上形成机翼前缘单涡结构；涡轴方向的速度分量不足以带走所有的自由剪切层时，多余的自由剪切层就会在前缘涡主涡外侧形成另一个的集中涡，此时在机翼翼面上出现前缘双涡结构。

4 结论

通过数值计算对机翼前缘后掠角为50°的中等后掠角三角翼布局的流场进行了分析，并得到以下结论：

1）对于中等后掠角三角翼，在一定的雷诺数和迎角下，机翼翼面上会出现前缘双涡结构。

2）前缘双涡结构的形成主要取决于三角翼前缘附近三维分离产生的自由剪切层强度和涡轴方向的速度分量之间的大小关系。

3）迎角较小时，在机翼上表面只是形成了一个集中涡；而随着迎角的增加，在机翼前缘涡主涡外侧会形成一个新的集中涡，此时翼面上出现前缘双涡结构；迎角进一步增大，涡层更多地被卷入内涡，同时由于前缘内涡以及其下二次涡的影响，最后当达到某一迎角时外涡消失，双涡结构消失。

［1］方宝瑞.飞机气动布局设计［M］.北京：航空工业出版社，1997.

［2］夏学湔，邓学蓥.工程分离流动力学［M］.北京航空航天大学出版社，1991：84－138.

［3］鲁素芬.50°后掠角三角翼流动结构及气动特性实验研究［D］.［硕士学位论文］.北京航空航天大学，2005.

［4］GURSUL I.Recent developments in delta wing aerodynamics［J］.TheAeronauticalJournal，2004，108：437－452.

［5］GORDNIER R E，VISBAL M R.Higher order compact difference scheme applied to the simulation of a low sweep delta wing flow［R］.AIAA Paper，2003－620，2003.

［6］温瑞英.近耦合鸭式布局鸭翼展向吹气间接涡控技术实验研究［D］.［博士学位论文］.北京航空航天大学，2008.

［7］AL－GARNI Ahmad Z，SAEED Farooq，AL－GARNI Abdullah M.Experimental and numerical investigation of 65°delta and 65°／40°double－delta wings［J］.Journalof Aircraft，2008，45（1）：71－76.

［8］SCHIAVETTA L A，BOELENS O J，CRIPPA S，et al.Shock effects on delta wing vortex breakdown［J］.JournalofAircraft，2009，46（3）：903－914.

［9］陈兰，王晋军.三角翼前缘涡轴向速度的数值模拟研究［J］.中国科学（E），2009，39（6）：1144－1151.

［10］杨立芝，高正红.三角翼大迎角流场结构和气动力特性的计算分析研究［J］.应用数学和力学，2005，26（6）：734－742.

［11］OELKER H C，HUMMEL D.Investigations on the vorticity sheets of a close－coupled delta－canard configuration［J］.JournalofAircraft，1989，26（7）：657－666.