基于Delaunay网格技术的松弛迭代粒子追踪算法

贾 攀，王 元，张 洋

（西安交通大学流体机械及工程系，陕西 西安 710049）

0 引言

作为一种非接触式的测量技术，PTV（Particle Tracking Velocimetry）已广泛用于多相流［1］、生物流体力学［2］等研究领域，成为实验流体力学的有力工具。PTV 算法着眼于离散粒子及其拉格朗日描述［3］，近年来取得了多样化的发展。应用PTV 算法分析高粒子浓度的PIV 流场图像一直是流场测量的一个研究方向［4］。目前提出的算法中，ORX（Original Relaxation Method）算法为此提供了一个很好的选择，它克服了一些常见算法的缺陷，可实现对剪切等复杂流场高浓度、高效率的测量［4］。Barnard 和Thompson［5］首先将ORX 用于标记实景测速，此后Lee和Back［3］率先应用ORX 分析湍流剪切流场，证实了ORX 对复杂流场处理的高效性；Ohmi 和Huang［4］通过对ORX 无匹配概率的迭代方式进行修正，提高了计算粒子团无匹配的准确率，提出了NRX（New Relaxation Method）算法；张洋等人［6］详细分析了NRX 中“孤粒子无匹配问题”的来源以及结果的伪逻辑性，提出了有效改进该问题的双向法则。应用NRX 为第1帧中的粒子在第2 帧中寻找匹配粒子时，首先需要给定两个固定阈值，分别用以确定临近目标粒子并与之保持相似运动形式的参选粒子集合和与目标粒子预匹配的候选粒子集合，这两个阈值的选取依赖于流场的参数，同时也和流场示踪粒子的分布情况有关，选取合理与否将直接影响匹配计算的准确率及效率。本文尝试应用DT（Delaunay Triangulation）方法确定候选和参选粒子集合来摆脱固定阈值以提高算法的独立性，并通过模拟二维应变流动中的单极涡运动进行了全面验证。

1 结合双向法则的NRX的基本原理

NRX 的原理如图1所示。记录连续运动的两帧图像分别记为X、Y，其粒子形心坐标分别表示为坐标矢量x、y。第1帧中第i个粒子的坐标矢量为xi，第2帧中第j个粒子的坐标矢量为yj；目标是为第1帧中任一粒子xi在第2帧中寻找匹配粒子，步骤如下：

第一步，确定目标粒子xi的参选和候选粒子集合。设候选粒子及参选粒子矢量的个数分别为Mi、Ni，候选粒子和参选粒子集合分别为Sc、Sr：

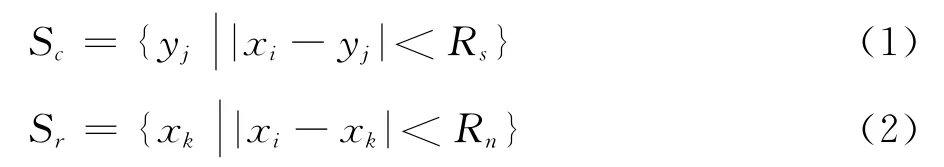
如图1所示，Rs和Rn分别为用以圈选候选粒子矢量和参选粒子矢量的阈值，意义为：xi真正的匹配粒子位于以Rs为半径的圆内；以Rn为半径的圆内的粒子真实位移矢量“拟平行”［3］。

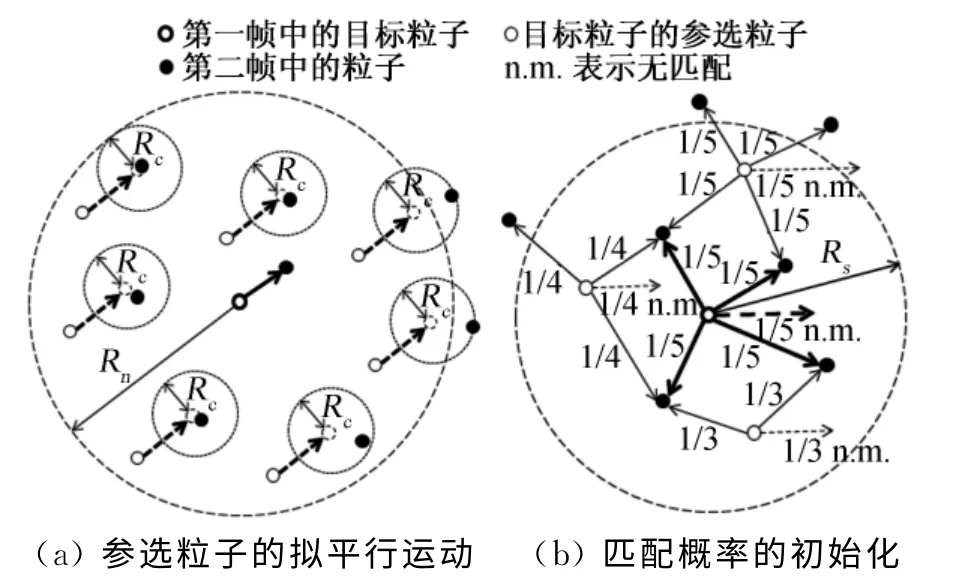
图1 NRX算法原理Fig.1 Algorithm for NRX

第二步，迭代概率初始化。设xi和yj匹配的概率为Pij；xi的无匹配概率为，由概率的归一化准则：

通过对计算效率和加权预判进行折衷考虑，为了简单起见，迭代初值和按如下格式确定：

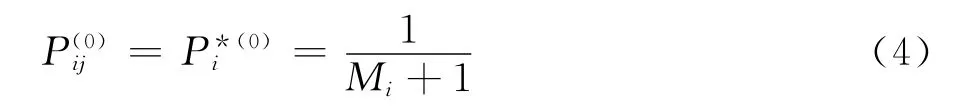
如图1（b）所示迭代初始值，箭头表示匹配，数字为概率大小，n.m.表示“无匹配”。

第三步，对xi的所有Pij以及迭代运算：

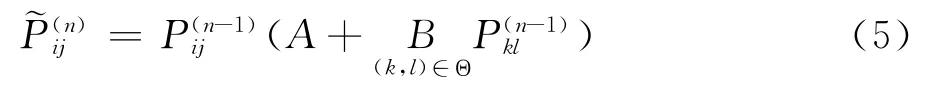
A＝0.3，B＝3，分别为松弛迭代的衰减和增益系数［4］。Θ 为参选位移矢量的集合：

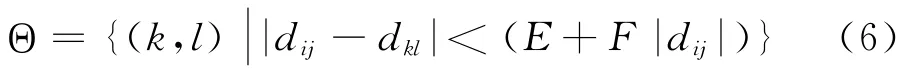
其中dij＝xi－yj，dkl＝xk－xl，E、F均为常数。其形式是全局量E（由流场具体情况决定）与局部量（F＝0.05）之和，从而能更好地适应速度梯度较大的流场［4］，图1（a）中Rc＝E＋F｜dij｜。

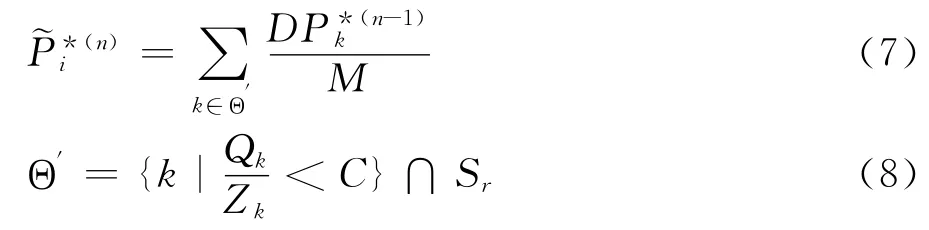
其中，Qk和Zk表示xk的参选位移矢量个数和其所有参选粒子的候选粒子总数，C、D为经验常数。迭代得到和之后，归一化：

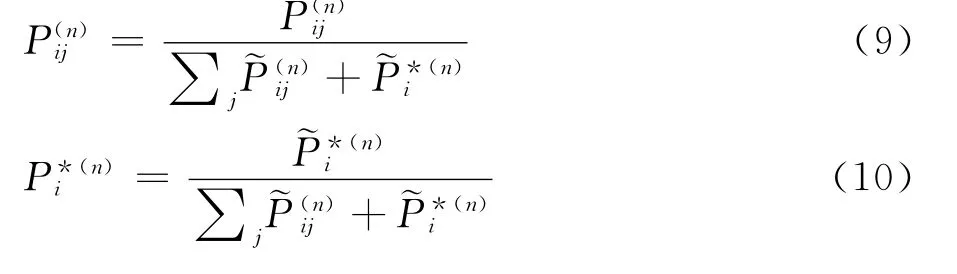
至此，xi的所有匹配概率一次迭代完成。然后重复第三步，直至各匹配概率收敛。xi的匹配对象为代表最大概率的yi（或无匹配）。对第1帧图像X中的每个粒子进行第一至第三步计算，得到X到Y的匹配结果。然后根据双向法则［6］，按照上述步骤再次计算得到Y到X的匹配结果，合并两份结果并统一至X到Y的模式，最后进行概率择优，得到最终的匹配结果。

2 应用DT 方法确定参选和候选粒子集合

如前文所述，应用NRX 时，需先确定两个阈值Rs和Rn，分别用以确定参选和候选参选粒子集合。Rs可取值为两帧时间间隔内粒子可能的最大位移，一般来说，通过对所测流场的基本分析和半定量的估计，可以得到比较合理的Rs，然而Rn并没有明确的确定方法，一般都是通过考虑流场粒子示踪的平均距离以及算法的计算效率经验地给定一个估计值［3－4］，这种经验性的方法实际中不便应用，选取的准确与否对算法的效率等也会有明显的影响。为了减少NRX对具体流场参数的依赖从而使之通用化，本文尝试引入DT 方法确定参选和候选粒子集合。

DT 方法主要用于处理离散点的问题，目前广泛用于有限元分析和图像的插值问题［7］。DT 方法是将离散点有效连接为平面三角形或空间三棱锥，形成非结构化网格［7］。目前DT 网格的生成方法很多，主要有Lawson算法和Bowyer－Watson算法［8］。此外，DT 方法生成的网格具有很好的“空圆特性”，即DT网格中任一三角形的外接圆范围内不会有其它节点的存在［7］。

设目标粒子为xi，确定参选粒子集合的方法为：以第1帧图像X中的粒子为节点生成DT 网格，然后选取网格中所有直接和xi相连形成三角形的粒子组成参选粒子集合。相似地，可确定候选粒子集合：首先将xi置于第2帧图像Y中形成新的离散点集并生成DT 网格，然后选取与xi直接相连形成三角形的粒子组成候选粒子集合。将xi置于第2帧图像形成新的点集时需要判断是否与第2帧中的粒子重合，若重合，则要作相应的处理保证候选粒子集合中包括该重合粒子。

3 自定义图像

通过模拟二维应变流动中的单极涡流运动［9］验证DT 方法的有效性。根据运动方程，生成匹配关系明确且粒子分布均匀的两帧自定义流场图像［10］。选取典型流动形式分别为剪切流动、旋转流动以及双曲流动。设图像大小为a，图像粒子总数为Np，定义容积率Pv为图像像素总数与粒子数目之比，即Pv＝a2／Np，显然a一定的情况下，Pv越小，粒子数Np越大。为保证粒子的数目，应用无粘连粒子生成法生成第1帧图像；然后根据给定的运动规律，生成第2帧图像，同时，为模拟图像噪音，对第二帧图像进行随机“添加”和“抹除”处理，定义“添加”和“抹除”的粒子数与第1帧粒子总数的比值分别为添加率μa和抹除率μd。在容积率Pv递变和引入干扰的前提下，分别应用DT 方法和传统固定阈值方法确定参选和候选粒子集合进行匹配计算，并与真实情况比较从而判断优劣。图2所示为三种自定义流场图像，其中图像边长a＝256像素、pv＝21.8524。

图2 自定义流场图像Fig.2 Self－defintion flow field images

4 计算结果及分析

4.1 DT方法确定参选粒子集合的有效性验证

按照前文所述方法，3种流场分别采用10种容积率，同时取添加率μa＝15%、抹除率μd＝10%，生成30组图像对。然后，分别应用固定阈值Rn和DT两种方法确定参选粒子集合，应用式（1）确定候选粒子集合，对自定义流场图像进行双向匹配计算［6］，相关参数见表1。通过对3种流场共630 种工况进行匹配计算，结果表明3种流场的计算结果都定性的一致，故此处仅针对旋转流场的匹配结果进行讨论。

表1 图像及算法相关参数（Ⅰ）Table 1 Parameters for images and algorithm（Ⅰ）

定义正确匹配矢量总数和第1帧粒子总数的比值为匹配准确率η。对所有工况的计算准确率进行分析，结果表明：应用固定阈值确定参选粒子集合时，在Rn的变化范围内，准确率η的变化趋势定性一致，并且都可保持在96%以上；应用DT 方法确定参选粒子集合时，准确率η也可达到96%以上，也表现出和固定阈值情况下一致的变化趋势。图3所示为4种不同的Rn以及DT 方法确定参选粒子集合时，双向匹配计算［6］的准确率η随容积率Pv的变化趋势，图示可知：5种情况下，准确率η都保持在较高水平，并且变化趋势都随容积率的降低有所减小。因此，与合理选取的固定阈值Rn一样，DT 方法也可在较大的容积率Pv范围内有效地确定参选粒子集合，计算结果保持高的匹配准确率。

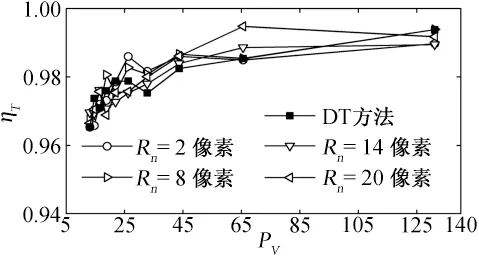
图3 准确率随容积率的变化趋势Fig.3 Tendency of matching accuracy

假设相同的条件下，N种工况的计算时间为ti，tmax＝max｛ti｜i＝1～N｝，通过对时间无量纲化定义计算效率ηT＝1－ti／tmax，显然，最大的计算时间对应的计算效率为0。对所有工况的计算时间进行分析，结果表明：一方面，应用固定阈值选取参选粒子集合时，各个固定阈值Rn下，ηT随Pv的减小而减小，这是因为随着Pv的减小，粒子数目增加，数据的处理量增大；对于固定的容积率Pv，计算效率ηT随着固定阈值Rn的增大有所降低，这是由于随着Rn的增大圈选的参选粒子的数量增加，数据处理量增加，并且这种现象随着Pv取值的减小逐渐显著；然而当固定阈值Rn取值过小（Rn＜5像素）时，计算效率会明显降低，这是因为固定阈值过小时，不能有效地确定参选粒子集合，双向计算［6］概率择优模块的耗时过大。另一方面，应用DT 方法确定参选粒子集合时，计算效率ηT也随容积率Pv的变化趋势与固定阈值情况下一致，并且对于给定的容积率Pv，应用DT 方法确定参选粒子集合时计算效率达到最高。

图4所示为4种不同的Rn以及DT 方法确定参选粒子集合时，双向匹配计算［6］的计算效率ηT随容积率Pv的变化趋势，图示可知：5种情况下，计算效率ηT都随容积率Pv的减小而减小；Rn＝2像素时，由于取值过小，计算效率最低；DT 方法确定参选粒子集合时，计算效率最高。

如图5所示为应用DT 方法和Rn＝9像素确定参选粒子集合时计算效率ηT随Pv的变化趋势，Δη表示DT 方法与固定阈值Rn相比计算效率的提高。图示结果表明：计算效率的提高Δη随容积率Pv的降低明显上升。

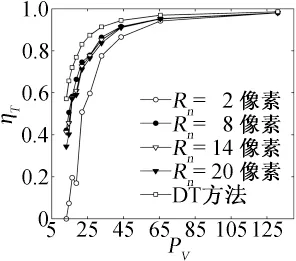
图4 计算效率的变化趋势Fig.4 Tendency of matching efficiency

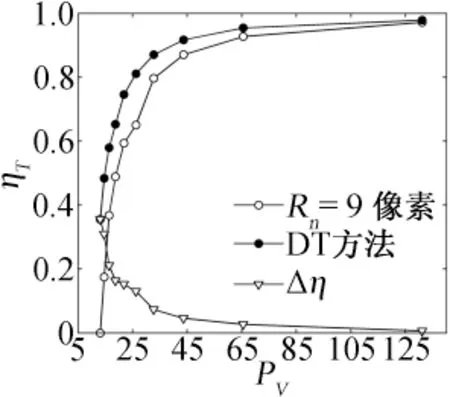
图5 两种方法计算效率比较Fig.5 Matching efficiency comparison

NRX 算法假设互相临近的粒子的位移“拟平行”，这也是确定参选粒子集合的准则。DT 方法以粒子为节点生成三角形网格，DT 网格的“空圆特性”保证了与目标粒子xi直接相连形成三角形的粒子也是几何上临近的粒子，这种“就近性”选取原则和NRX 的假设是一致的。因此，应用DT 方法和固定阈值确定参选粒子集合的物理本质是一致的，DT 方法可以有效地确定参选粒子集合，并且DT 方法可以自适应容积率Pv的变化确定合理的参选粒子集合，显示出对高粒子浓度粒子图像分析的高效性。

4.2 DT方法确定候选粒子集合的有效性验证

首先，按照前文所述的方法，每种流场采用10种容积率，每种容积率采用8种粒子帧间最大位移，取添加率μa＝15%、抹除率μd＝10%，生成3种自定义流场共240对图像。然后，分别应用式（1）和DT 方法确定候选粒子集合，应用式（2）确定参选粒子集合，对自定义流场图像进行双向匹配计算［6］，相关参数见表2。通过对3种流场共480组工况进行匹配计算，结果表明，3种流场的计算结果都定性一致，故此处仅针对旋转流场的匹配结果进行讨论。

表2 图像和算法的相关参数（Ⅱ）Table 2 Parameters for images and algorithm（Ⅱ）

图6所示为容积率Pv＝16.384，粒子最大位移m＝6像素时，旋转流场的匹配计算结果。图6（a）为应用固定阈值方法确定候选粒子集合时的计算结果，匹配准确率η为97.45%，可以看出计算错误矢量基本上是随机分布在图像中，数量较少；图6（b）为应用DT 方法确定候选粒子集合的情况下的计算结果，匹配准确率 仅为86.26%，从图6（b）中可以看出计算错误矢量明显多于图6（a）的情况，且绝大部分的错误匹配矢量在粒子位移较大的位置出现，这是由于真正匹配粒子和目标粒子xi之间的距离较大，DT 方法“就近性”确定的候选粒子集合中包含真正匹配粒子的概率减小。

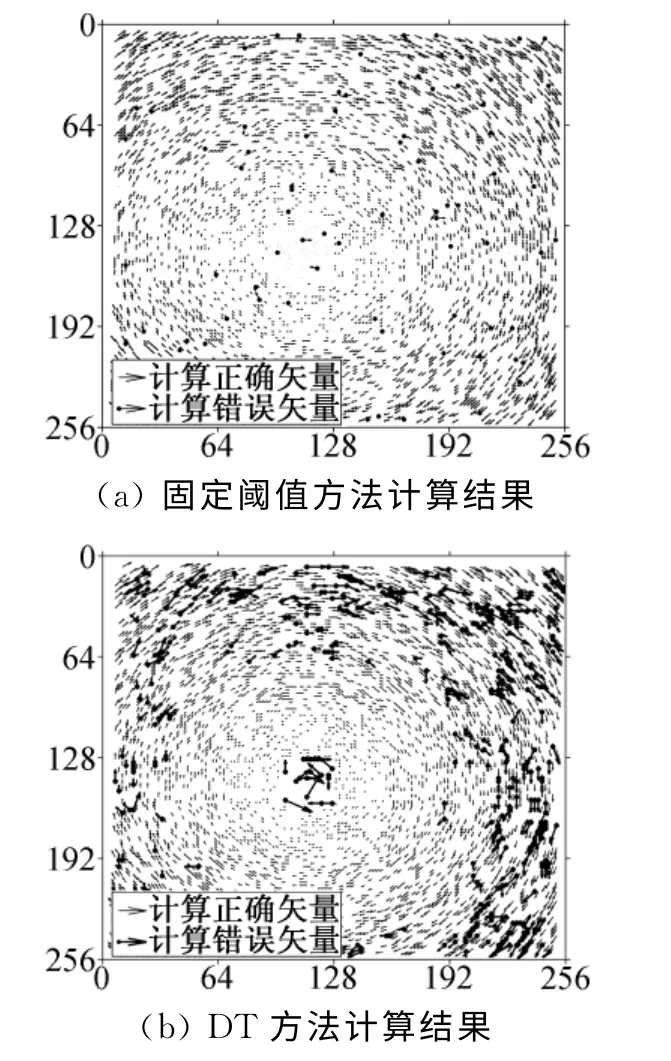
图6 匹配结果比较Fig.6 Comparison of the matching results

对计算结果分析，结果表明：一方面，应用固定阈值确定候选粒子集合情况下，m在其变化范围内固定取值时η随Pv的降低有所减小；Pv在变化范围内固定取值时，η随m的增大而基本保持不变。另一方面，应用DT 方法确定候选粒子集合时，η随Pv的降低而减小，并且减小的幅度大于应用固定阈值确定候选粒子的情况；并且η随m的增大明显减小。

图7所示为m＝6像素时，旋转流场匹配准确率η随Pv的变化趋势。ηN和ηD分别为应用固定阈值Rs和DT 方法确定候选粒子集合情况下，准确率随Pv的变化曲线。图示可知：ηN在Pv变化范围内始终保持在95%以上，说明只要根据粒子的最大位移m合理地选取固定阈Rs，就可有效的确定候选粒子集合；然而，ηD仅当容积率Pv较高时保持高的值，随着Pv进一步降低，ηD则呈现明显的下降趋势，当Pv接近10时，ηD低于85%，这是因为随着Pv的持续减小，粒子浓度增大，目标粒子xi附近的非真正匹配粒子增多，DT 网格中目标粒子和真正匹配粒子直接连接形成三角形的概率下降。

图8所示为Pv＝16.384时，旋转流场匹配准确率η随m的变化趋势。ηN和ηD分别为应用固定阈值Rs和DT 方法确定候选粒子集合情况下，η随m的变化曲线。图示可知：ηN在m变化范围内始终保持在95%以上，说明只要对流场进行基本分析，合理估计粒子最大位移m，给出合理的阈值Rs，就可得到合理的候选粒子集合；而然，ηD则随m的增大呈现明显的下降趋势，这是由于随着m的增大，DT 网格中真正匹配粒子和目标粒子的距离也增大，DT 方法“就近性”的确定候选粒子集合的缺陷也更加突出。

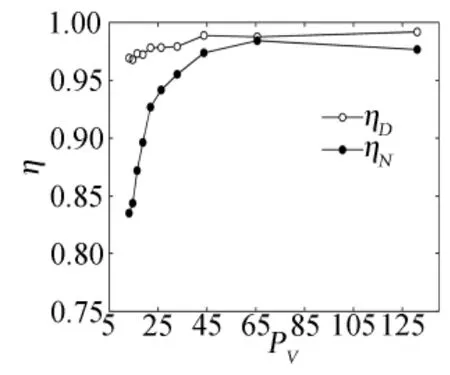
图7 准确率随Pv 的变化Fig.7 Tendency of matching accuracy with Pv

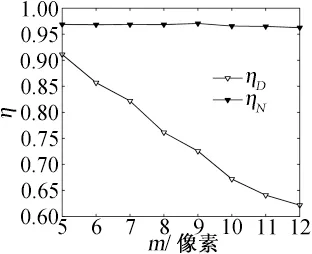
图8 准确率随m 的变化Fig.8 Tendency of matching accuracy with m

综合以上分析可知：若要提高准确率，一方面需提高粒子图像的容积率，但是这一点和松弛迭代算法处理复杂流场高浓度粒子图像的优点相悖；另一方面是减小帧间粒子位移，对于特定的流场，则需要提高粒子图像的采样频率，这对实验平台的图像采集系统提出更加苛刻的要求，同时也会加大数据的处理量。

候选粒子集合中应该包括目标粒子的真实匹配粒子，实际应用NRX 时，若可对流场进行基本分析，给定恰当的阈值，就可得到合理的候选粒子集合。DT 方法时仅从几何位置出发确定候选粒子集合，由于DT 网格的“空圆特性”，选取的粒子都在位置上临近目标粒子，然而对于一些复杂的流场情况，由于间粒子的最大位移m较大，真实的匹配粒子位于距目标粒子较远的位置。因此，DT 方法这种“就近性”选取的特点与确定候选粒子的物理背景不统一，不能合理地确定候选粒子集合。

5 结论

（1）由于DT 网格的“空圆特性”所致的“就近性”选取参选粒子特征的与NRX 中确定参选粒子集合的物理本质一致，DT 方法可以有效地确定参选粒子集合。

（2）DT 方法不能有效地确定候选粒子集合，由于DT 网格的“就近性”选取的特点与NRX 确定的候选粒子集合中必须包含真正的候选粒子的物理背景不一致，并且这种矛盾在容积率降低、帧间粒子位移增大的情况下更加突出。

（3）在NRX 的基础上应用DT 方法确定参选粒子集合提出一种新的DT－NRX 算法。DT 方法引入减少了一个固定阈值的确定，提高了算法的独立性。DT－NRX 与NRX 算法比较表明：一方面，与NRX 类似，DT－NRX对容积率变化有很好的适应性保证了算法准确率高的特点，另一方面，DT 方法可以自适应容积率的变化有效地确定参选粒子集合，表现出对高粒子浓度流场图像的分析的高效性。

［1］TSUJI T，MIYAUCHI T，OH S，et al.Simultaneous measurement of particle motion and temperature in twodimensional fluidized bed with heat transfer［J］.Kona PowderandParticleJournal，2010，28（28）：167－179.

［2］EVANGELOS B，MICHELE G，UFUK O，et al.CFD and PTV steady flow investigation in an anatomically accurate abdominal aortic aneurysm［J］.JournalofBiomechanicalEngineering，2009，131（1）：1－15.

［3］BEAK S J，LEE S J.A new two－frame particle tracking algorithm using match probability［J］.Experimentsin Fluids，1996，22（1）：23－32.

［4］OHMI K，LI H Y.Particle－tracking velocimetry with new algorithms［J］.MeasurementScienceandTechnology，2000，11（6）：603－616.

［5］BARNARD S T，THOMPSON W B.Disparity analysis of images［J］.IEEETrans.PatternAnalysisMachine Intelligence，1980，2（4）：333－340.

［6］张洋，王元，李志强.结合双向法则的松弛迭代粒子追踪测速法［J］.空气动力学学报，2010，28（3）：250－254.

［7］马逸尘，梅立泉，王阿霞.偏微分方程现代数值方法［M］.北京：科学出版社，2006：25－29.

［8］WASTON D F.Computing the n dimensional DelaunayTessellation with application to Voronoi ploytopes［J］.ComputerJournal，1981，24（2）：167－172.

［9］TRELING R，BECKERS M，Van HEIJST.Dynamics of monopolar vortices in a strain flow［J］.Journalof FluidMechanics，1997，345：165－201.

［10］OKAMOTO K，NISHIO S，SAGA T，et al.Standard images for particle－image velocimetry［J］.Measurement ScienceandTechnology，2000，11（6）：685－691.