马赫数变化对平板上方柱绕流特性的影响

薛大文，陈志华，孙晓晖，韩珺礼

（南京理工大学瞬态物理重点实验室，南京 210094）

0 引言

方柱作为飞行器表面凸起的典型外形，其绕流特性与对飞行器的影响一直受到研究与关注，特别是对超声速与高超声速方柱绕流及其所包含的激波与边界层相互作用等的研究，不仅具有理论价值，而且还有实际的工程应用背景。

自20世纪50年代开始，人们进行了大量的风洞试验和飞行实验以研究超声速流动问题。因受实验与计算条件的限制，其流场细节与分离机理等仍没完全揭示清楚。早在1968年，Young等［1］实验研究了超声速钝舵的激波边界层干扰，并测得平板表面压力分布。Dolling与Bogdonoff［2］同样对前缘为半圆柱的钝舵超声速绕流进行了实验测量，并给出了钝舵前缘的压力双峰型分布以及平面表面的压力。随后，Shigeru等［3］研究了超声速条件下尖舵和钝舵绕流的激波－边界层干扰，实验所得的压力分布以及油流图谱显示了干扰区的不稳定性，同时实验利用彩色油流技术证实了二次分离的存在。Barberis等［4］研究比较了钝舵后掠角对干扰流场影响，实验所得的一系列纹影图和油流图谱显示了后掠角的增大可以有效减小干扰强度和干扰范围。王世芬等［5］对超声速圆柱绕流进行了系列实验研究，得到了物面平均压力和热流分布。而李素循［6］对高超声速与超声速下，有高度变化的圆柱与方柱进行了风洞实验研究，得到了比较详细的平板表面的压力分布、物面油流图谱和纹影照片。

随着计算机技术的发展，数值模拟在此领域的应用越来越广泛。Hung［7］用MacCormack格式先后模拟了平板上圆形钝舵和方舵的超声速流场，计算结果与实验结果比较吻合，但是由于MacCormack 格式的固有缺点，结果对激波分辨率不高。Chaussee等［8］利用雷诺平均方法先后模拟了圆锥、再入式飞行器、航天飞机等绕流流场，计算了升阻力与压力分布。同样邓小刚［9］基于三维雷诺平均方法，利用NND 格式对方舵超声速绕流激波边界层干扰进行了模拟，结果描述了弓形激波和分离激波碰撞后所形成的“λ”波系结构并分析了流场的弱非定常性。马汉东等［10］同样基于雷诺平均法与修正的ROE 方法，对高超声速且壁面有传热条件下的高超声速圆柱绕流进行了数值模拟，得到了上游分离区的马蹄形五涡结构及二次分离激波。李艳丽［11］也用雷诺平均方程模拟了高超声速钝舵层流干扰，并与风洞试验数据做了对比，研究了干扰流场的流动特性以及前缘后掠角对流场的影响，随着后掠角的减小，干扰流场区域扩大，压力载荷也逐渐增加。Shen等［12］同样基于雷诺平均方程，利用WENO 格式对有压缩拐角的柱／锥体高超声速流动的激波边界层干扰进行了研究，对比讨论了WENO 格式阶数对模拟精度的影响，与实验结果的对比显示了5阶WENO 格式的精度明显高于3阶格式。

虽然前人对超声速绕流问题做了不少数值研究，但大多基于雷诺平均方程，只能得到各流场参数的统计平均量，丢失了包含在脉动运动中的大量有重要意义的信息。大涡模拟方法则通过体积平均，对大尺度运动直接计算，而对于比网格尺度小的小尺度运动对大尺度运动的影响则通过建立模型来模拟。因而既具有较直接模拟少得多的计算量，同时还可保证模拟流场的精确性。因而本文就采用近年来发展较快的大涡模拟方法，同时利用WENO 格式来模拟前人研究较少的方柱绕流问题，结合采用自适应网格加密技术（AMR，Adaptive Mesh Refinement）对方柱超声速绕流及其激波－边界层干扰流场进行模拟计算，进一步研究和讨论来流马赫数对其流场结构的影响。

1 计算方法与模型

1.1 计算方法

三维可压N－S方程经过Faver滤波，略去非线性项后，得到以下形式：连续性方程：

动量方程：

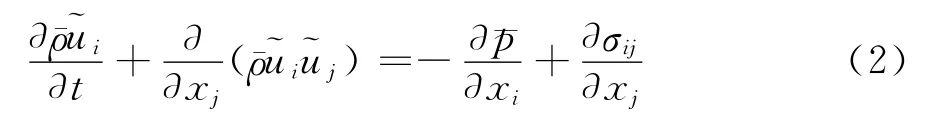
能量方程：

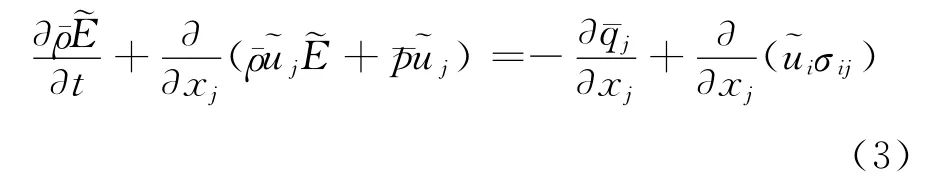
上述数学模型在无量纲化后，采用有限体积法进行离散。时间推进采用三阶精度的Runge－Kutta法，对流项采用三阶WENO 格式，而粘性项则用中心差分格式。计算过程中还对网格进行自适应加密来提高时间与空间的求解效率。计算过程中还对高压力梯度区域采取自适应加密［13］来提高对激波的分辨率。

1.2 三维计算模型

选用平板上方柱绕流的计算模型为文献［6］中的FD－03风洞实验模型，具体结构与计算域如图1 所示。计算域的长×宽×高大小为33cm×24cm×10cm，方柱根部与来流入口距离为16.8cm，方柱截面大小为2.5cm×2.5cm，高度为3cm。分别取来流马赫数Ma＝2.9与5.0。

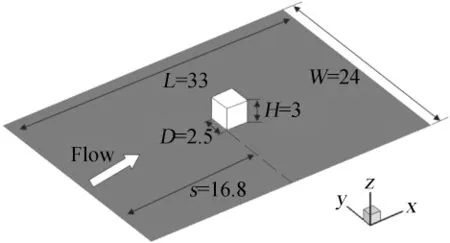
图1 计算模型图（单位：cm）Fig.1 Computational model（unit：cm）

2 计算结果与讨论

图2为Ma＝5时，方柱的实验纹影（图2（a））与本文的计算结果（图2（b））比较。可知，两者非常吻合。对于高超声速方柱绕流（Ma＝5.0），方柱前端的二维弓形激波贴近柱体迎风面，形成激波层。同时，计算能够清晰揭示流场中分离激波和三维弓形激波碰撞后所形成的类“λ”波系结构，以及柱体绕流过程中的复杂波系结构。

图3为不同马赫数（Ma＝2.9，5.0）条件下，三维方柱绕流的压力等势分布的切片与平板压力分布。两种情况下的柱体前端压力分布总体趋势相同，即方柱顶端前半部分与弓形激波之间以及方柱前端底部存在高压区。同时，分离激波与方柱顶端弓形激波的相交位置基本相同。但受来流影响，高超声速来流的弓形激波弯曲程度较低马赫数大。而平板上压力分布具有相同趋势。相关讨论参见本节后面。

图2 Ma＝5.0时，方柱绕流的实验纹影（a）与本文的计算结果（b）比较Fig.2 Comparison of experimental［6］and numerical schlieren at Ma＝5.0

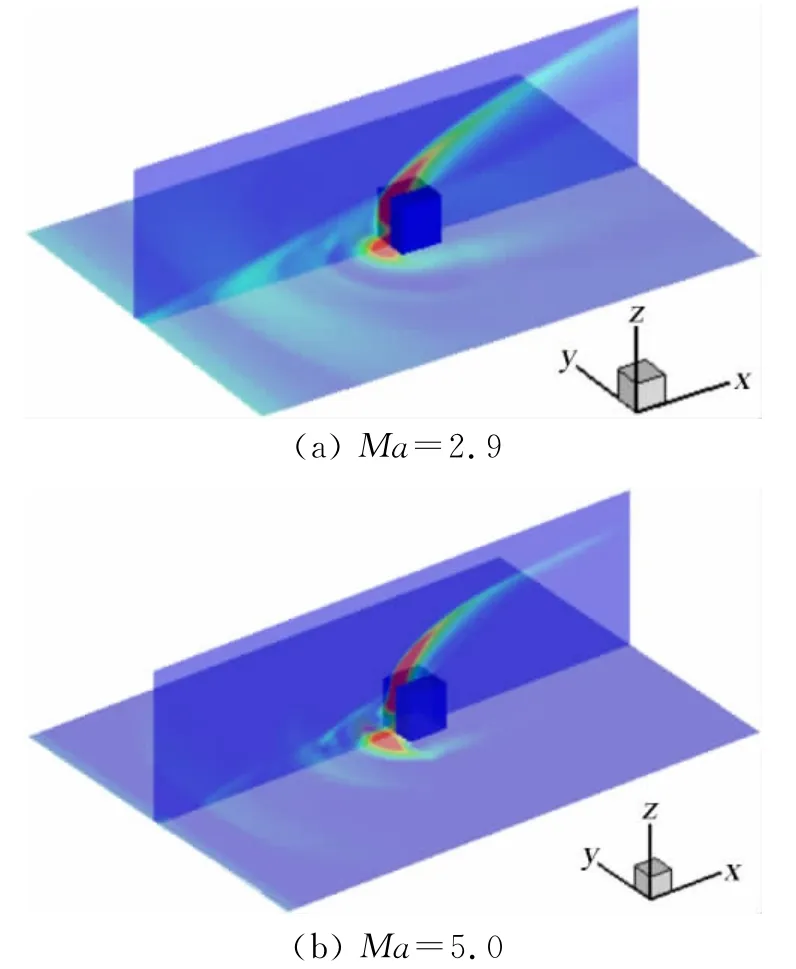
图3 马赫数Ma＝2.9，5.0时，方柱三维绕流的压力切片与平板压分布图Fig.3 Three－dimensional pressure distribution of the cylinder at Ma＝2.9and 5.0

图4为两种马赫数条件下的方柱上游平板对称线上的压力计算值与Ma＝5.0时的压力实验值的比较。图中以方柱迎风面处作为横坐标原点，同时取x／d（其中d为方柱宽度）作为横坐标，以p／p∞为纵坐标。可知，对于Ma＝5.0，数值模拟结果和实验基本相符，但在x＝－1.0～－2.75区间内相差相对较大，这主要是由于此区域的旋涡的非定常发展与变化造成的，因此，此区域的压力一直处于脉动状态（参见图6与图7）。另外，柱体上游平板对称线上的压力同样与测试相符，并呈双峰值分布，最高峰值点靠近柱体表面。而在距柱体较远的上游处，x≤－2.75，计算值与实验值完全相符。一般地，压力随着与柱体的距离变小而增大，约在x／d＝－1.8处达到第一峰值。此位置点正好产生逆压梯度而引起流动的二次分离。且在第一峰值和最高峰值之间又有极小值出现，此处应是涡核下部高速低压区。随后由于临近柱面，压力值迅速上升，由于柱体前缘根部角落涡的存在，在靠近柱面处压力又由极大值又开始下降。来流马赫数Ma＝2.9时，压力双峰的基本特征和Ma＝5.0时相似，且第一峰值相差不大，压力抬升点也大致相同，但是第二峰值之间的差异较大，随着马赫数变小，数值下降较多。图5 为方柱前缘对称线上的压力分布。由于分离激波位置刚好略高于方柱顶部，因此在z／d约为1.4处形成压力极大值。同样，计算值和实验数据吻合良好。这在Ma＝5.0和Ma＝2.9两种不同马赫数下，柱体前端压力分布趋势基本一致。但随着马赫数减小，压力峰值有所下降。

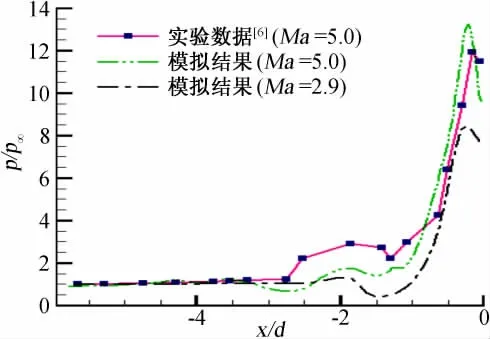
图4 方柱上游平板对称线压力分布Fig.4 The pressure distribution along the symmetry axis of the flat

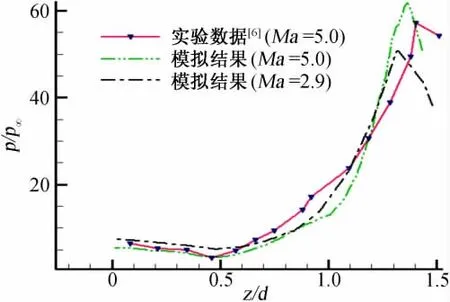
图5 方柱前缘表面对称线压力分布Fig.5 The pressure distribution on the leading edge of cylinder

图6和7分别为Ma＝5.0与2.9时，平板表面（xoy面）及柱体对称面（xoz面）上的流线分布。可知，流体经过激波或遇到方柱障碍后出现了逆压梯度，并导致分离，在柱体上游的平板表面形成了典型的分离与再附的拓扑结构。图中S 表示分离点，A表示再附点，S2、A2、S3、S4分别表示二次、三次与四次分离和再附点。以上各图每个分离点对应一条分离线，而再附点和再附线相对应。表面摩擦线收拢于分离线，并从再附线发散，均符合鞍点和结点交替出现的拓扑规律［14］。另外，图6与图7 的xoz面还显示了不同时刻方柱前端分离区流场的形成与发展。

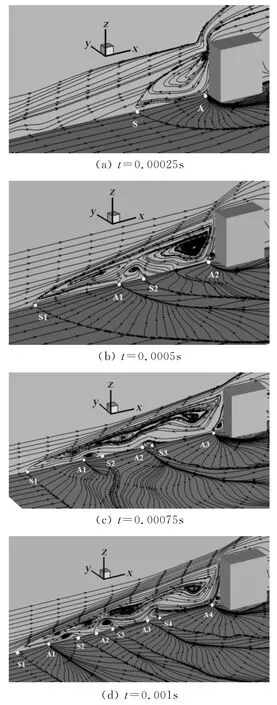
图6 Ma＝5.0时，平板表面及对称面流线图Fig.6 Streamlines on both the surface of the flat and the symmetry plane at Ma＝5.0

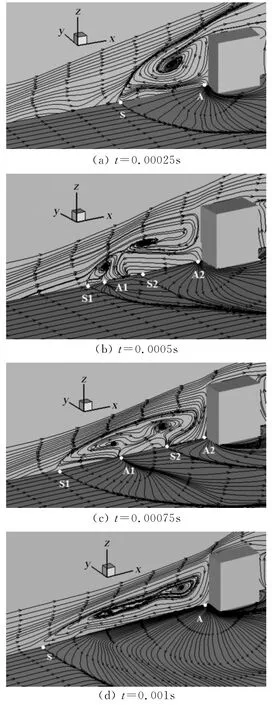
图7 Ma＝2.9时，平板表面及对称面流线图Fig.7 Streamlines on both the surface of the flat and the symmetry plane at Ma＝2.9

障碍物绕流分离区中的旋涡数量和旋涡结构一直是被关注且尚未完全解决的问题。Sedney［15］认为Reynolds数的不同会导致分离区内旋涡个数的变化，当二次分离现象被发现以后，Sedney又认为主涡将分叉并以偶数方式增加。后来Norman提出了喷流迷宫模型，认为主涡可以分叉为两个同向的旋涡，但不会产生二次分离，由此产生了奇数个旋涡。邓小刚等［11］模拟方舵激波诱导湍流边界层分离流场结构时，得到流动发展经过2 涡－4涡－6涡－4涡的发展过程并将继续变化。

图6与图7中所描述的方柱分离区的流场结构表明了分离区流动的高瞬态特性。t＝0.00025s时，马蹄涡结构开始形成，随着分离区的往上游发展，主涡与边界层作用，涡管变小，形成新的逆压梯度，并造成二次分离，产生两个顺时针涡及其中间的逆时针反向涡（见图6（b）），与此同时在方柱前缘的角落涡以及逆时针涡的影响下，与其相邻的两个顺时针涡被迫抬升，迫使壁面流动再次分离，最终形成图6（c）、图6（d）中所显示多涡结构。结合xoy和xoz平面可以看到每一个马蹄涡涡管都对应于一条分离线和一条再附线，随着时间的发展，分离区中的旋涡数目由2个到4个到6个再到8个，结构也越来越复杂，进而表现为表面流线在保持拓扑结构的同时越来越扭曲。

对比图7与图6，两图中各涡的形成相似，但由于来流马赫数变小，激波边界层干扰明显减弱，表现为分离区长度变小，分离区中涡系结构变得相对简单。从图7（d）中看到，来流马赫数较小时，分离区的涡被抬升，因而仅在平板表面留下一条分离线和一条再附线。

为了能形象描绘方柱上游分离区流场结构的三维特性，我们结合流线与压力等势分布，对此区域内的主要特征进行了显示。图8为t＝0.001s时，不同马赫数（Ma＝2.9，5.0）的方柱绕流分离区及附近的空间流线与压力等势分布。图8（a）显示了分离区中四个顺时针方向涡管的空间流线形态，而图8（b）则刻画了两个顺时针方向涡形态，揭示了分离流场中各点缠绕着向下游蜿蜒，形成横向的翼展状结构。各流线分布趋势大致相同，在方柱阻碍和逆时针涡作用下，从上游往下游，流线位置开始抬升。图中三个平面上的彩色代表压力等势分布，其中红色代表压力值最高区，蓝色则为最低区。结合图6和图7，可知每条分离线位置对应一个压力峰值，弓形激波与柱面的迎风面及顶端前半部分则对应流场中的压力极大值，而平板表面拓扑结构中的各条流线正是空间结构的各涡所留下的蜿蜒扭曲的“足迹”。

方柱绕流的尾涡形态同样被关注。图9 为t＝0.001s时，不同马赫数（Ma＝2.9，5.0）的柱体下游尾涡空间流线图。流线以压力值着色。对于高超声速方柱绕流（Ma＝5.0，图9.（a）），贴近柱体背风面的涡对由其下部流线以螺旋形态往上抬升同时往下游发展，形成的近壁“羊角状”尾涡对，另一对则从柱体两侧下部绕至柱体背风面后从下部往上抬升以螺旋形态沿着涡轴线往外散开并一直持续下去，从而形成远壁“喇叭状”尾涡对。而对于超声速方柱绕流（Ma＝2.9，图9（b）），柱体尾部可以清晰地看到由下往上螺旋发展的“羊角状”涡对，而往下游的“喇叭状”涡对则不明显。相比可知，马赫数较大时，柱体尾涡大幅摆动，呈现外扩形态，而小马赫数的尾涡线则显得狭长。图10为对应时刻两种马赫数条件下，方柱尾流在平板表面上的流线分布。同样清晰显示了两种情况下尾流的异同。在靠近柱体壁面流线形态大致相同。但在远离方柱的下游，对于Ma＝5.0时，由于其螺旋形态“喇叭状”涡对的影响，在平板表面留下了曲折的再附线，而Ma＝2.9时的再附线却显得直接明了和有序。

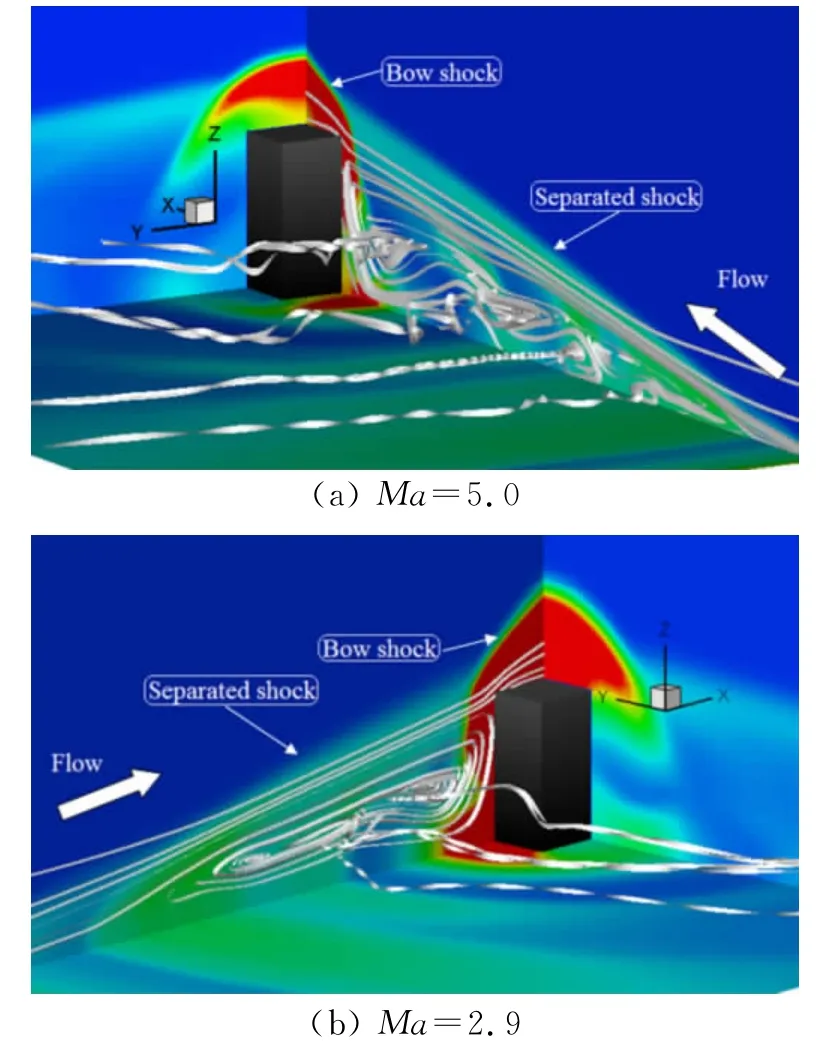
图8 t＝0.001s时刻柱体上游的空间流线形态Fig.8 Three－dimensional streamlines in front of the cylinder at time t＝0.001s

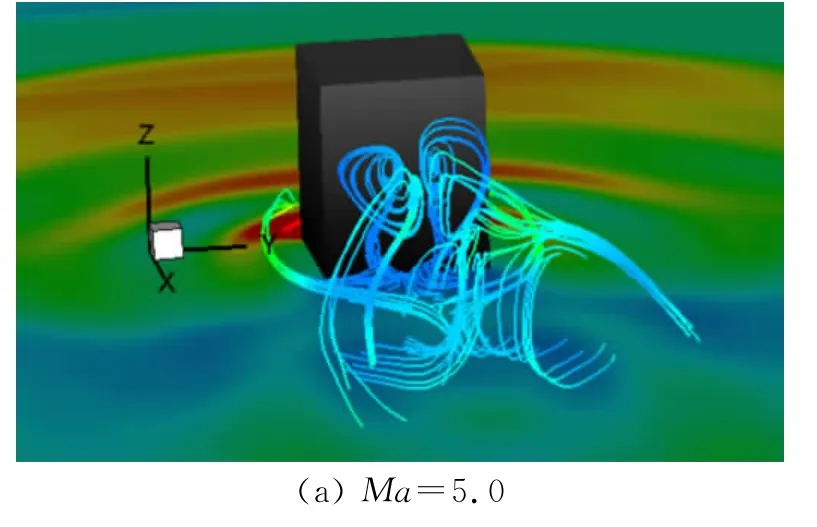
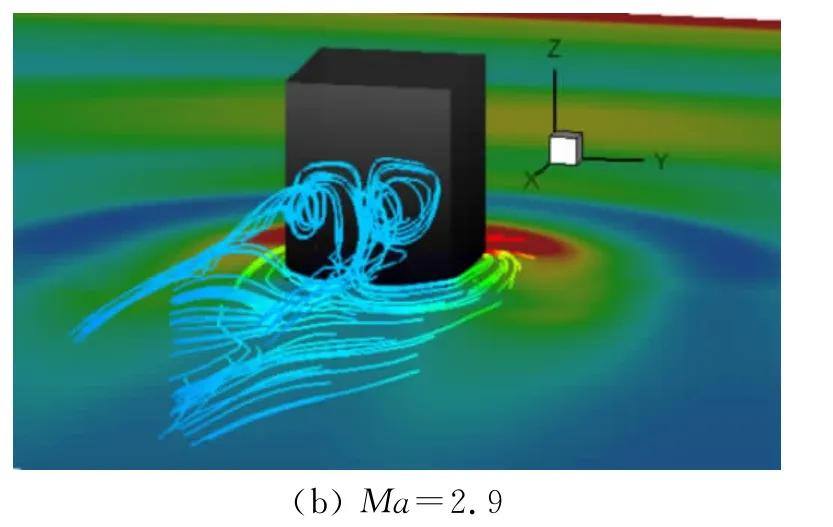
图9 t＝0.001s时刻，方柱尾流的空间形态Fig.9 Wake behind the cylinder at time t＝0.001s

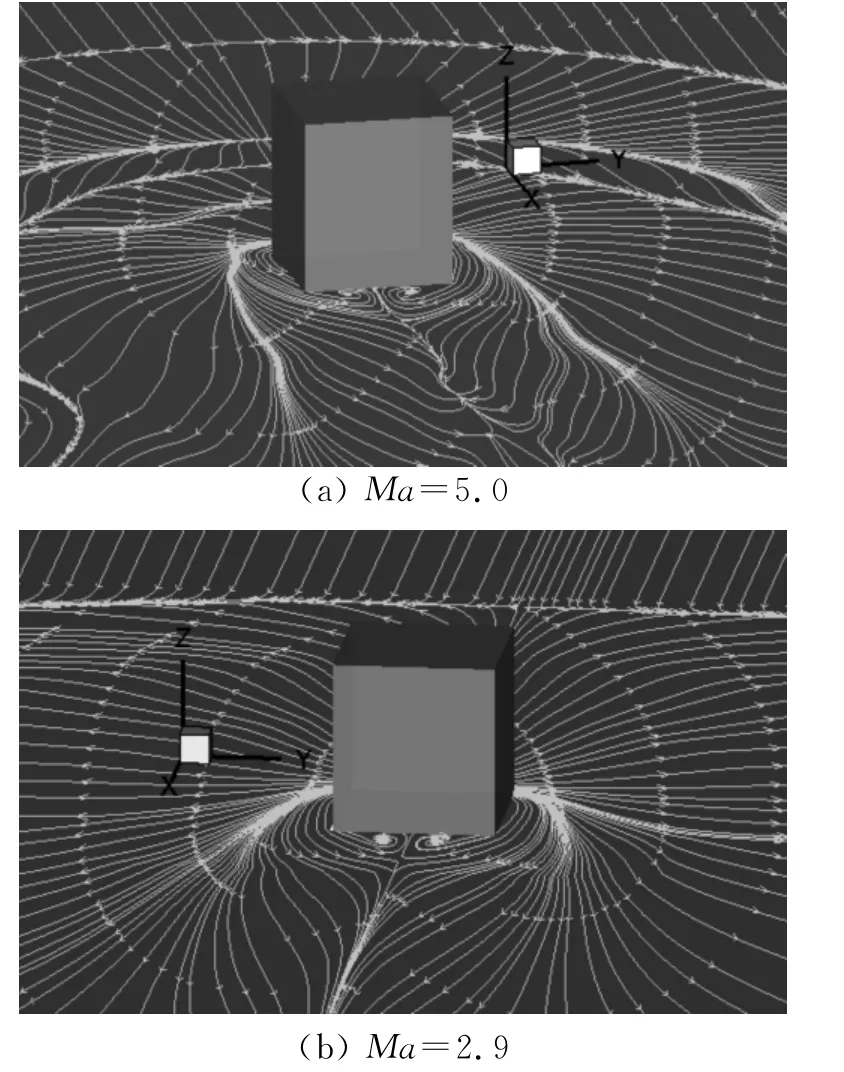
图10 t＝0.001s时刻，方柱尾流的平板表面流线分布Fig.10 Streamlines of the wake on the flat at time t＝0.001s

3 结论

本文通过大涡模拟方法，应用WENO 格式以及自适应网格加密技术，对来流马赫数，Ma＝2.9，5.0条件下的三维方柱超声速绕流进行了数值研究，与相关实验结果相符。数值结果表明，两种来流条件下，柱体前端平板上的压力分布具有相同趋势，一般随与柱体距离变小而增大，而最高峰值点靠近柱体表面，但Ma＝2.9的压力最高峰值下降较多。另外，对于Ma＝5.0来流，激波边界层干扰明显，表现为分离区长度较大，分离区中涡系结构复杂，分离区中的旋涡数目由2个到4个到6个再到8个，拓扑结构扭曲，其绕流尾涡形态同样较为复杂，柱体尾涡大幅摆动，呈现外扩形态，而Ma＝2.9的尾涡线则显得狭长。

［1］YOUNG F L，KAUFMAN L G，ROBERT H K.Experimental investigation of interactions between blunt fin shock waves and adjacent boundary layers at Mach numbers 3and 5［R］.OHIO：Aerospace Research Labs Wright－Patterson，1968.

［2］DOLLING D S，BOGDONOFF S M.Blunt fin－induced shock wave／turbulent boundary－layer interaction［J］.AIAAJournal，1982，20（12）：1674－1680.

［3］SHIGERU A，SYOZO M，SATOSHI O.Intensive studies on unsteady secondary separations and oscillating shock waves in three－dimensional shock waves／turbulent boundary layer interaction region induced by sharp／blunt fins［R］.AIAA－93－2939.

［4］BARBERIS D，MOLTON P.Shock wave－turbulent boundary layer interaction in a three dimensional flow［R］.AIAA－95－0227.

［5］王世芬，王宇.钝缘舵高超音速湍流分离特性［J］.航空学报，1996，17（S1）：2－7.

［6］李素循.激波与边界层主导的复杂流动［M］.北京：科学出版社，2007：68－80.

［7］HUNG C M，BUNING D G.Simulation of blunt－fininduced shock wave and turbulent boundary－layer interaction［J］.JournalofFluidMechanics，1985，154：163－185.

［8］DENNY S，CHAUSSE E.High－speed flow calculations past 3－D configurations based on the Reynolds averaged Navier－Stokes equations［R］.NASA－100082，1988.

［9］邓小刚，张涵信.数值研究平板方舵激波－湍流边界层干扰［J］.力学学报，1993，25（6）：651－657.

［10］马汉东，李素循，吴礼义.高超声速绕平板上直立圆柱流动特性研究［J］.宇航学报，2000，21（1）：1－5.

［11］李艳丽，李素循.高超声速绕钝舵层流干扰流场特性研究［J］.宇航学报，2007，28（6）：1472－1478.

［12］SHEN Y Q，ZHA G C，MANUEL A H.Simulation of hypersonic shock wave／boundary layer interaction using high order WENO scheme［R］.AIAA 2010－1047.

［13］BERGER M，COLELLA P.Local adaptive mesh refinement for shock hydrodynamics［J］.JournalofComputer＆Physics，1988，82：64－84.

［14］张涵信.分离流与旋涡运动的结构分析［M］.北京：国防工业出版社，2005：18－22.

［15］SEDNEY R.A survey of the effects of small protuberance in boundary layer flows［J］.AIAAJournal，1973，2（6）：782－792.