二重积分计算公式的一个推导方法
中国劳动关系学院数学与计算机教学部 郑红芬 贾屹峰
直角坐标系下二重积分化为二次积分,是重积分的基础,传统的方法是通过计算平行截面面积已知立体的体积完成的。在[2]中,采用的坐标系不是常见的,而且推导过程中需要把立体的图形平面化,使得部分学生难以理解。这里采用生活中常见的切片面包作为实物模型,利用元素法直接计算曲顶柱体的体积,得到二重积分的计算公式,将抽象的知识具体化,并在实际教学过程中得以应用,取得了很好的效果。
根据二重积分的几何意义,二重积分的计算归结为求曲顶柱体的体积。图1 所示的面包外形是曲顶柱体,我们以此为具体的实物模型,计算曲顶柱体的体积。
图2 是图1 面包所对应的曲顶柱体。设曲顶所对应的曲面方程为z=f(x,y),其在xOy面上的投影D是Y型区域,即:
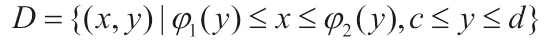
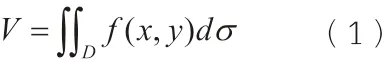
图1 中的面包是切片面包,在图2 中,相当于用一组垂直于y轴的平面 截曲顶柱体,将其分割成n个薄曲顶柱体,其中,y0=c,yn=d,且y0<y1<…<yn
如果能够算出所有面包片的体积V(yi),代入上式,即可求得整个面包的体积V。从图2 中任取一个薄曲顶柱体,如图3。
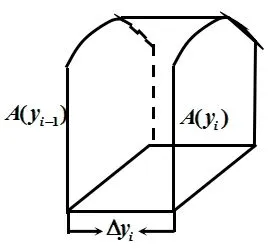
图3
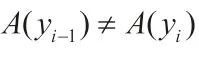
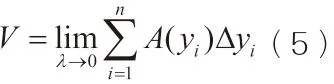
其中,A(y)是垂直于y轴的平面截曲顶柱体所得的截面积。
如果能够求出截面积A(y),代入(7)式,就可以计算出曲顶柱体的体积。为了求截面积A(y),首先需要知道截面是什么图形,任取一个面包片,把它的外形画在黑板上,如图4。
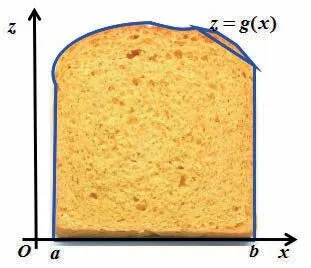
图4
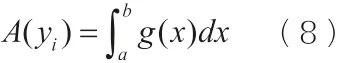
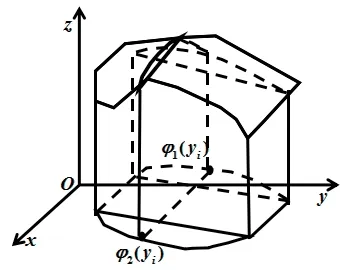
图5

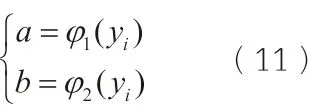
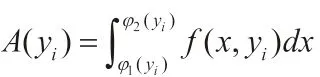
则任一垂直于y轴的平面,截曲顶柱体所得的截面面积为
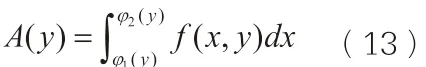
把上式代入(7)式,可得曲顶柱体的体积
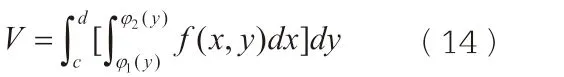
曲顶柱体的体积也就是二重积分的值,进一步可以写成:
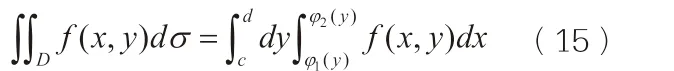
从而,二重积分就化为了二次积分,f(x,y)<0,上式仍然成立,因此,(15)式就是Y 型区域二重积分的计算公式。
以切片面包辅助推导二重积分计算公式具有非常好的直观性,学生获得丰富的感性认识,在把课本上的知识同现实生活结合起来的同时,使得高等数学不再枯燥,激发了学生学习高等数学课程的兴趣。

