以基本图形为载体，培养学生直观想象

福建省厦门市金鸡亭中学 郭小霞

核心素养指的是人适应未来社会生存和发展所需要的必备品格、关键能力，数学核心素养就是在数学学科中的必备品格与关键能力，这对于学生学习至关重要。高中数学课标中指出数学核心素养包含六个部分：数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析。直观想象在初中教学阶段主要体现在空间观念和几何直观的培养。本文笔者以基本图形为载体，浅谈如何培养学生的空间观念和几何直观，进一步发展学生的直观想象。

一、课标中有关空间观念和几何直观的阐述和要求

数学课程标准（2011 版）中指出：空间观念是指根据物体特征抽象出几何图形，根据几何图形想象所描述的实际物体；想象出物体的方位和相互之间的位置关系；描述图形的运动和变化；依据语言的描述画出图形等。

几何直观主要指的是利用图形描述和分析问题，借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要作用。

发展直观想象，落实为空间观念与几何直观的测量目标有：（1）能根据条件画简单平面图形；（2）理解几何图形的运动和变化；（3）能从较复杂的图形中分解出基本图形，并能分析其中的基本元素之间的关系；（4）运用简单图形的性质揭示复杂图形的性质。

二、借助基本图形，发展学生直观想象

1.基本图形的认识和教学

（1）什么是基本图形

在几何分析中，组成一个几何问题的图形的最简单、最基本但又具有特定性质，能明确地阐明其应用条件和应用方法的图形，称为基本图形。基本图形蕴含在重要几何定理中，每个几何定理都有三种语言，包括文字语言、图形语言和符号语言。我们还可以将常见几何图形的叠加约定为基本图形，如一线三等角等。

（2）如何教学基本图形

我们可以围绕某个知识点形成系列基本图组，对于每个基本图形，我们可以按照以下脉络进行研究：基本图形→图形性质→位置特征→应用条件→应用方法。

2.以基本图形为载体，渗透分析法解决问题

怎样在一道几何综合题中找到基本图形的应用条件和应用方法，即什么情况下会想到用哪个基本图形，怎么用这个基本图形？这是技能到能力转化的关键，也就是思维内化。我们有两种解决问题的方式：由因导果综合法和执果索因分析法。我们要用“你是怎么想？”“为什么这么想？”“怎么会想到？”等问题进一步引导学生提高解决问题的思维品质，达到思维内化。

3.利用基本图形寻找添加辅助线的方法

用基本图形解决辅助线添加问题，我们的着眼点不再聚焦在作为图形的局部的“线”上，而是着眼到一个完整的“图形”上。添加辅助线不仅仅是一个添线问题，更是一个补形的问题，添加辅助线的实质是基本图形完整化的结果。

三、提高学生直观想象的有效措施

提高学生直观想象，就要提高学生的空间观念和几何直观，教学中应注重以下三方面：

1.教学中应注重对重要定理进行总结

在探究归纳完定理时，要注重对定理本身进行深入的分析和总结：

延续性护理能满足健康照护需求，有利于病情恢复[2]，提升了患者的满意度，也提升了患者对医护人员的信任度，增加了医患之间的互动，对于患者病情的恢复起到一定的作用，对于患者疾病的后续护理有莫大的帮助[3]。延续性护理作为临床医疗护理工作的重要延伸，体现了医护人员对患者的人性化服务[4]。

（1）注重几何定理的三种语言（文字、符号和图形）之间的相互转化，将定理的条件标在图形中，将知识进行图示化和可视化，同时也要将这些定理及图形进行模型化和形象化，如同位角“F”型，内错角“Z”型，同旁内角“U”型，角平分线“鸡爪”型，三角形的外角“小旗帜”型，等腰三角形三线合一“屋顶”型，线段的垂直平分线性质“小雨伞”型，角平分线的性质“纸飞机”型等，可以让学生来抽象命名，加深印象，又增加了课堂趣味。

（2）注重引导学生分析定理的条件和结论，分析定理的源与流，了解定理的使用范围、注意事项和用途，什么时候可以使用这个定理，使用这个定理可以解决什么问题等等。如三角形的中位线定理，从定理的结论我们可以知道，这个定理的用途是证明线段平行或线段二倍（或一半）关系。从定理的题设我们可以知道，“三角形”和“中位线”这两个条件是缺一不可的，因此在碰到要求证线段平行或线段二倍（或一半）关系的几何题时，我们常见的辅助线做法有：①题目中有涉及中点连线但没有三角形的情况，这时要连接三角形的边，构造三角形。②题目中有涉及三角形、中点，但没有中位线,这时我们要作中点的连线，构造中位线。

2.教学中应注重对重要例（习）题进行归纳

在讲完例题或是做完习题后，应重视引导学生对一题或一组题从以下4 个方面进行归纳：

（1）注重基本模型的提炼

在教学中，注重让学生总结例题和练习中的基本模型，如“一线三等角”的基本模型，能更好地解决全等三角形乃至后续要学习的相似三角形的证明和计算问题。直角三角形及斜边的高所分的两个直角三角形所构成的子母型相似的基本图形等，都是初中几何证明和计算常考的内容，通过题组的形式，让学生对基本图形进行提炼和归纳，有利于学生更敏锐地找到解题方向。

（2）注重基本思路的引导

在解决四边形问题时候，我们经常引导学生将四边形的问题通过连接对角线等转化为三角形问题，这个转化学生较为熟悉，也掌握得较好，而有时候我们也会将三角形问题转化为四边形来解决，而这类辅助线做法学生较为陌生，因此，要及时归纳这类问题的基本思路，有利于学生更好地理解和灵活应用。

在《平行四边形》这章中，证明三角形中位线定理时，我们是通过构造平行四边形，将三角形的问题转化为平行四边形的问题，利用平行四边形的性质得到三角形中位线定理；证明直角三角形斜边上的中线等于斜边的一半，我们是将直角三角形的问题转化为矩形问题，利用矩形性质进行证明。教师应结合这两个定理的证明，注重引导学生去归纳做这类辅助线的思路。让学生观察这两题的证明方法，体会辅助线做法，并以问题加以引导：“倍长中位线和倍长中线的共同特征是什么？”（倍长和中点）“做这类辅助线有什么好处？”（可得到全等三角形和平行四边形）“什么时候要考虑做这种辅助线？”让学生去总结归纳，发现其中的规律，化未知为已知，进一步提高学生分析问题和解决问题的能力。

（3）注重基本结论的联想

在讲评例题和练习时，应注重结论的发散联想，了解可得到这个结论的多种途径，再挑选适当的路径求解或证明。如《平行四边形》这一章涉及线段二倍（或一半）关系的定理有3 条，可以引导学生归纳（如图1）。又如要证明矩形，常常要用证明90°，要注重90°的联想，如图2。

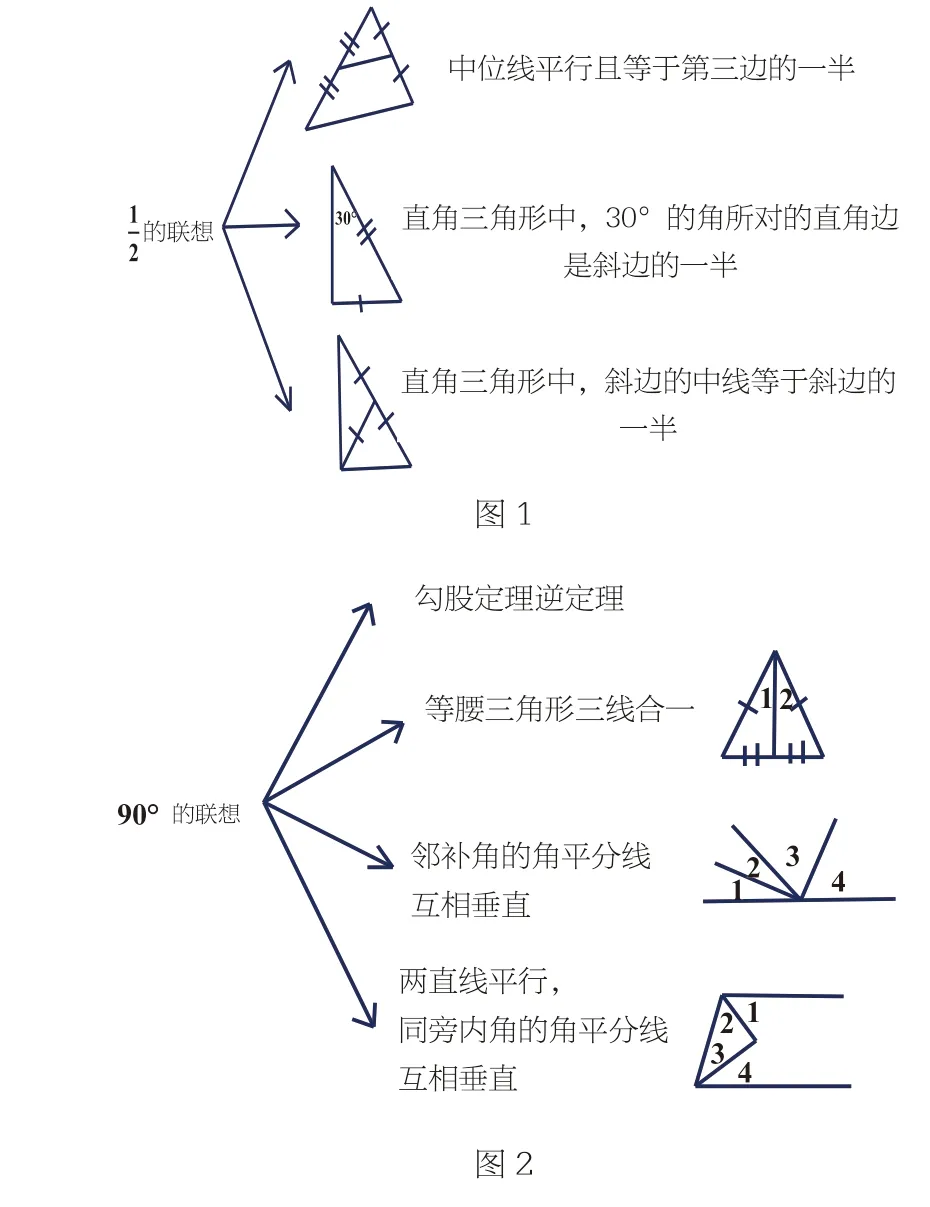
（4）注重基本载体的挖掘

初中几何中某些特殊的图形具有独特的性质，往往利用这些性质可以便于证明和求解，因此要注重对基本载体的挖掘。如正方形是最特殊的平行四边形，它具有一切平行四边形所具有的性质，常以正方形为载体证明三角形全等问题，可以以题组的形式引导学生去挖掘正方形这个载体为全等三角形的证明提供了哪些线段相等，哪些角相等。

3.教学中应注重学生作图能力的培养

在教学实践中，笔者发现很多中等或中下的孩子能从较为复杂的图形中分离出几个基本图形，但是还不会找到它们之间的关系，只是从局部看这些基本模型，把题目隔开间断碎片化。笔者尝试让学生根据题意重新作图，在慢慢画图的过程中找出基本图形及基本图形之间的联系，逐步将这些基本模型重组和串联起来。因此，在初中几何教学过程中，还应注重学生作图能力的培养，在讲例题或习题时，有意识地将图形去掉，让学生根据题意画图，既能加深学生对题意的理解，又能更好地分离出基本图形，通过基本图形把题目串联起来，发现基本图形之间的联系，从全局看问题，更完整、更全面地理解题目。在平时教学中，提倡让孩子把新学的基本图形纳入之前的基本图形题库中，进行组合编题，提高学生的兴趣和直观想象能力。

新课程标准在“图形与几何”方面提出应注重发展学生的空间观念和几何直观，提高学生的直观想象，从复杂图形中分离出基本图形，以基本图形为载体抓住本质和重点，正确提取和重组，从而提高学生的识图和画图能力，进而提高直观想象能力。