模型思想在初中几何教学中的运用及反思
浙江省长兴县古城中学 章 明
一、背景及意义
1.随着新课程改革的深入,古城中学的初中数学教师结合学情特点,积极开展培养学生自主学习能力的课堂教学。笔者在初三几何知识具有概念化、抽象化、模式化的认识特征的基础上,渗透模型思想在几何教学中的运用。有效培养学生把数学的概念结论和处理方法进行从一般向特殊的推广和应用 ,全面提高了初中生的数学素养。
2.几何是数学知识的重要组成部分,从小学阶段开始就有着直观形象的图形认识。在不断学习跟进过程中,几何知识应用在了更广泛的学习领域。教学中发现,学生对形象思维的几何问题会处理得十分正确,而对“K 型”“三垂型”这种相似基本图形的认识还没有达到更深入的理解。尤其是当它出现在与函数结合的问题时,学生受思维拓展的限制,无法在知识的迁移中完成创新应用。运用模型思想,构建“K”型相似在几何课堂教学中的应用,可以有效突破教学中的难点。
二、模型思想在初中几何教学中的运用
1.复习讨论,提炼模型
课堂教学中,教师对学生的思维引领是探究新知的关键。在“K型”模型思想的渗透课堂教学构建中,可以先让学生复习一下相似三角形的内容,讲讲预习卡上几个题目的思路。例如:(1)如图1,Rt △ABC中,∠ACB=90°,AC=BC,直线MN经过点C,作AD⊥MN于D,BE⊥MN于E,AB=5,AD=4,则BE是_____;(2)如图2,AB⊥BD,CD⊥BD,AB=2,CD=6 ,E是BD上一点,DE=4 且满足AE⊥CE,则BE=____。

图1
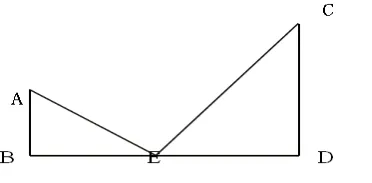
图2
在学生结合复习题进行小组讨论的过程中,教师要抛出诱发学生思维拓展的问题。例如:为什么这两个三角形全等?说一下理由;说说相似的理由;证明相似的过程中关键是证明了一组锐角相等,其依据是什么?彻底打开学生对三角形相关的知识记忆,为新授课的思维拓展做好了铺垫。源于复习中的问题都涉及两个直角三角形相似,共有“三处地方是垂直”的特点,加深了学生在思想认识上的统一。
2.合作探究,融会贯通
学生对知识的驾驭能力在于对知识点的融会贯通,教学中要充分利用学习小组合作探究的作用,提高学生的解题水平。例如教师在多媒体上出示课件:
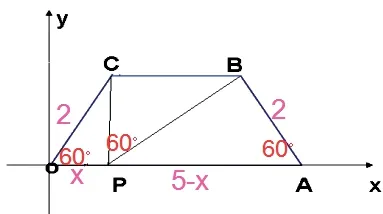
图3
如图3,直角坐标系中,四边形OABC是等腰梯形,BC∥OA,OA=5,AB=2,∠COA=∠CPB=60°,点P为x轴上一个动点(不与点O、点A重合),求这时点P的坐标。
针对这个图形的出现和问题的提出,教师不要急于指出问题的关键所在,而是发挥小组合作学习的优势进行讨论:要求点P坐标,关键是求出什么?是否存在两个三角形相似?是哪两个?给出学生对图形特点足够的观察时间,让学生在合作交流中,对“K 型为骨架,而且在两边及中间位置存在三个相等角,那么两个三角形相似” 的特点加强认识,从而加深学生对“K”型相似的深刻理解,有效提高学生的抽象思维能力,为正确解题做好了铺垫。教师在学生对知识难点逐个突破之后,要适时进行类比总结,利用多媒体展示自制的贴近学情的课件,加强对学生在几何学习中的模式思想,如PPT 课件所示。

3.自主学习,实践应用
学生数学知识的有效提高在于解题技能的熟练程度以及在实践中进行知识的创新应用。课堂教学对知识的应用是学生提高自主学习能力的最好时机。教师给出相应的检测题目,要求学生自主完成。教师可以在学生真实的学习信息反馈中了解新授课的教学得失,进行及时有效的质疑补漏,并且结合新授课的要点进行重点突出的形象直观的课堂小结,例如运用多媒体的课件展示功能以文字概括、图形比对的形式再次梳理知识(参看PPT 课件),辅助学生真正理解对模型思想在初中几何教学中的运用,以便尽快转换成学生解答这类问题的能力。

三、模型思想在初中几何教学中运用的教学反思
随着课堂教学改革的深入,一线教师要积极转变教学理念,创建新型的授课模式。在教材教法和课堂教学模式的构建中,突破传统的教学方法。笔者执教的“模型思想在初中几何教学中的应用”得到了同行和专家的认可,为古城中学第七届品质课堂展示活动争得了荣誉,最重要的是模型思想在几何教学中的渗透,极大地启发了初中教师在处理教材内容时如何使用正确有效的方式、方法。本节课的成功讲授仅仅是为今后教师执行课堂教学改革抛砖引玉。基于相似三角形在整个初中数学知识中的重要地位,笔者选取小专题“K 型相似在几何中的应用”开展教学,主要目的在于对初三学生数学素养的培养,做好学生思维方向的过渡。反思模型思想在教学中的应用策略,有以下几点与同仁们分享:(1)选题集中,重点突出。首先让学生对“K”型的认识经历由浅入深、由特殊到一般的过程,从而确定相似模型,而后在应用模型解决问题时,由尝试应用到思维拓展,让学生进一步巩固方法技能,拓宽思维,提升能力。(2)注重师生互动,与学生为本,充分发挥学生的主观能动性。题目出示后,放手让学生先思考,再让学生充分表达意见,最后教师给予点拨指导。(3)思想方法突出。本节课渗透了多种思想方法,在对“K”型的认识过程中,体现从特殊到一般的认知规律;在思维拓展中,对于“在抛物线上探究点P 使得以CP 为直径的圆恰好经过点B”的问题设计,就是在教学过程中先让学生动手找一找,再画一画,通过分析判断最终确定P 点位置,当符合条件的圆一旦画出,学生很容易根据图形得出新的结论,即∠PBC=90°,进而构造“三垂型”相似来解决问题,数形结合,构造法在该问题中得到充分运用。
模型思想在教学中的应用,不仅是教学改革中研究性课程教学的需要,更重要的是抓住初中学生的形象思维向抽象思维过渡的特点,运用模型思想在教学中的渗透,做好学生解题能力和聚合思维的培养。在多种学习方法的设计和多媒体教学工具的开发利用上,提高学生几何知识的运用能力,形成学生在实践中的创新技能培养,全面提高新时期初中生的数学素养。

