生活味，让数学课堂更生动

江苏省昆山震川高级中学 马玉红

在数学学习中，学生应该充分了解数学中的生活味，感受数学之美。教学中要将生活问题融入数学课堂教学中，让学生体验数学的魅力，提高学生解决数学问题的能力。

一、问题的探索

1.用一双善于发现生活中数学的眼睛，提高学生发现实际数学问题的能力

数学课程标准的要求之一是情境教学，这要求教师有敏锐的观察力，善于发现生活中的数学。让数学课堂生活味，把现实生活中学生感兴趣的事情进行加工、整理并运用到数学课堂中。

例如我在教学“数列的应用”时，就围绕“今天我买房”这个主题：房价上涨，手中只有十万元存款，现在需要买40 万元的房子，准备贷款买房。我让同学们到银行了解情况后，第二天告诉我具体办法。这样，教科书中缺乏关系的问题更加生动，学生有参与的动力，变被动学习数学为主动学习。通过这种方式，学生可以更好地理解数学的作用，感受到使用数学的乐趣。

2.有一双善于发现生活中数学的手，培养学生解决数学问题的能力

大部分学生在学习立体几何时都觉得太抽象，想象不出来。讲解立体几何时，我就让学生用硬纸板做生活中可以看见的立体图形，让他们对比自己手中的图形去学习立体几何性质，课后检测时大部分同学都能准确掌握有关概念与性质。

案例：在直三棱柱ABC—A1B1C1中，AB=BC= ，BB1=2，∠ABC=90°，E、F分别为AA1、C1B1的中点，沿棱柱的表面从E到F两点的最短路径的长度为_______________。

在做这道题时，我提示学生把以前做的几何体拿出来看看，剪剪试试，引导他们发现问题的实质，空间几何体中，无论这两个面夹角是多少度，两个面内各取一点，沿着交线折起，长度是不变的。利用平面内两点间直线的距离最短，这类问题就是把两个平面展平。

我马上把这个问题类比到圆锥上：一个圆锥的底面半径10cm，高为8cm，一只蚂蚁从底面圆上任意一点A出发，沿着圆锥的侧面爬行一周回到A点，所走的最短路程是多少？学生马上反应出来要将圆锥展开处理。

趁热打铁，拓展延伸到圆柱上：如图，蚂蚁从A点出发，沿着圆柱的侧面爬行两周到达B点，问最短距离是多少？

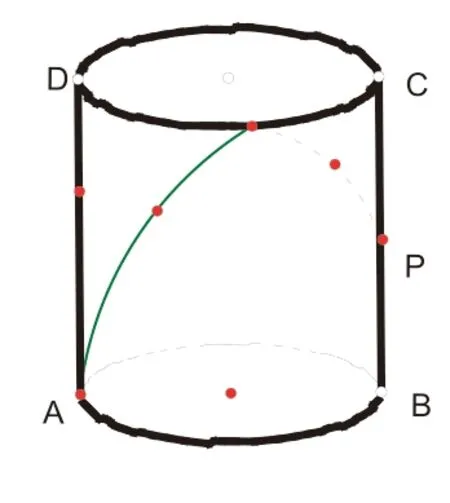
学生发现绕一圈是直接展开，两圈应展开两次。

再变形到：圆柱下表面封闭，母线和底面圆直径长均为2，BC中点P，在圆柱内壁P处有一粒米，外壁A处有蚂蚁，则蚂蚁吃到米所经过的最小路程为多少？

刚开始学生有点迷糊，这再展开一次、两次都没用，我给了提示：如果把容器看成是有内外两层的呢？学生马上就明白了，就是展开再对称。

以上三个题目是同一个道理，同学们发现动手能够解决数学问题，数学就在他们身边，同时，动手做出一件事物使得他们有一种成就感，享受成功的愉悦。通过自己动手操作获取知识，激发了学生体验数学生活的乐趣。

二、问题的解决

学生碰到生活中的问题会感觉到兴奋，解决了会有一种成就感。那么，怎么解决好生活中的数学问题呢？并不是只停留在学生动手上，而是要利用已经掌握的数学知识去指导解决实际问题。

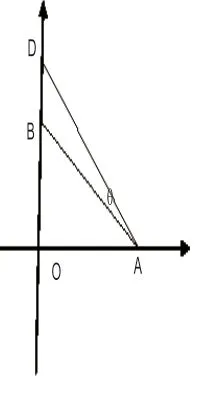
例如2010 年江苏卷第17 题，这个数学应用问题难于将实际问题转化为已经学过的数学，即把现实问题“数学化”。

分 析： ①求α-β最 大， 难 点 在 于α-β= ∠DEB， 这 样tan ∠DEB最大即∠DEB最大，即α-β最大。把问题数学化，问题常规化。

②联系课本题求∠θ最大。

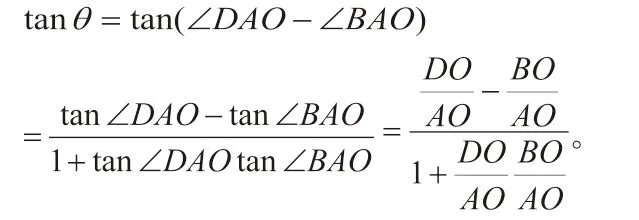
③问题推广：世界杯射门问题：AB为球门，球员在哪个区域射门命中率最高？

以上两个数学应用问题为同一题目，“数学化”后都可用②来解决。教学中，以上两个问题的解决反映出来两个问题：一是学生找不到切入口，即学生找不到问题的关键，不能把实际问题数学化；二是学生出不来，学生的计算能力较差，对最值问题处理不得当。所以在处理跟生活相关的应用问题时应该分为五个步骤：（1）审清题意；（2）建立数学模型；（3）用适当的方法进行计算；（4）检验答案是否符合实际意义；（5）作答。五个步骤中，学生最难攻克的是步骤（1），生活类应用题题目长，描述语言多，学生因为害怕而不愿意深思，抓不住重点，也就没有办法进入题目中，所以审题最重要，要先把题目缩减，长题变短，变成符合学生的口味，更容易建立数学模型。其次是步骤（3），应用题的表达式不像其他计算类题目式子那样简洁、有针对性，需要自己整理，一是学生没有整理意识；二是学生有畏难情绪。在教学中应该适当演示计算步骤，让学生掌握计算方法，会应用计算技巧，鼓励学生坚持算到底，培养学生的意志力。

三、问题的反思

教师要善于将生活问题与数学知识融合，加入课堂教学中，引导学生分析、思考，在学生活动中总结数学知识，实施教学过程。积极创设丰富有趣的情境，让学生体验数学，分析和解决现实生活中的问题，这样既能学好相关的数学知识，又能提高解决实际问题的能力。教师在课堂教学中引入的生活中的数学内容越丰富，课堂教学活动越生动，学生对数学学习更感兴趣，生活中的数学是课堂数学活动的动力源泉。