带有导数项非线性Schrödinger方程行波解的存在性
杨林林, 孙宗玉, 魏公明
(上海理工大学 理学院,上海 200093)
近年来,许多学者对非线性Schrödinger方程行波解的性质进行了研究.如Floer等[1]利用Lyapunov-Schmidt方法对一维不含导数项的非线性Schrödinger方程行波解的存在性进行了研究,随后 Oh[2-5]将其结论推广到高维情况;Ding等[6-7]和Rabinowitz[8]用变分法及山路引理证明了一类不含导数项的非线性Schrödinger方程行波解的存在性,Wang[9]进一步证明了这些行波解的集中性.本文推广了Floer等[1]的结论,证明了含一阶导数摄动项的非线性Schrödinger方程行波解的存在性和集中性,其中V,a(x)满足条件:

a.V是R上的连续有界函数;
b.a(x)是R上收敛于0的连续有界函数且a(x)∈C2(R);
c.a(0)=a′(0)=0
对 方 程 式 (1),找 其 形 式 为φ(x,t)=exp(-iEt/h)v(x)的解,其中v是实函数,函数V,E满足V-E>0.将φ(x,t)代入式(1),得

不失一般性,假设γ=m=1,则
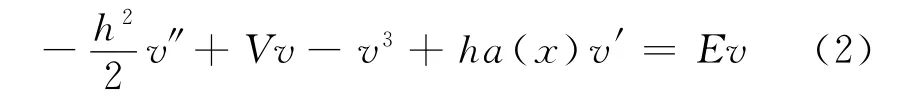
主要结论:
定理1 设x0是函数V的非退化临界点,V,a(x)满足上面的条件,则存在h0>0使得对满足0<h<h0的h,方程(2)有非零解;当h→0时,这些解关于x0越来越集中.
文中所使用的一些记号:
H=H2(R,R),L=L2(R,R)(H2,L2均 为Sobolev空间);(,)为L2内积;
1 线性估计

其中,λ=E-V(0),Vh=Vh(y)=V(hy),令
Sh(u)=a(hy)u′,则式(3)化为

易知,当h→0时,a(hy)→a(0)=0且Vh-V(0)在R的紧子集上一致收敛于0.对式(4)两端取极限,得其形式极限为
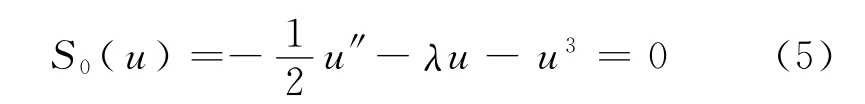
所以,Sh(u)是S0(u)的一个摄动,且S0(u)=0有两个解

采用Lyapunov-Schmidt方法,定义uz,h(y)=u0对足够小的h>0,找式(4)形式为uz,h+φ的解.由Taylor’s展式知

若uz,h+φ是式(4)的解,则Sh(uz,h+φ)=0.由 式 (6)知S′h(uz,h)φ= -Sh(uz,h)-Nz,h(φ),只需证明φ为-S′-1h(uz,h)(Sh(uz,h)+Nz,h(φ))的不动点即可.
下面给出几个重要引理和定理:
引理1[1]对任意的h>0,函数Sh是光滑映射,且其Fréchet导数为

证明 由H1嵌入到H、H嵌入到L6(Sobolev空间)为连续嵌入及H和L的定义,引理得证.
记S′0(uz,h) 的 核 为Kz,h, 则Kz,h=span{u′z,h}.记K⊥z,h为Kz,h在H上的L正交补,对于φz,h∈K⊥z,h∩H,定义π⊥z,h:L→K⊥z,h,Lz,h=π⊥z,hS′h(uz,h)|K⊥z,h∩H.
引理2[2]存在b>0,对任意满足V-E>b>0的E及u∈D(Hh),有
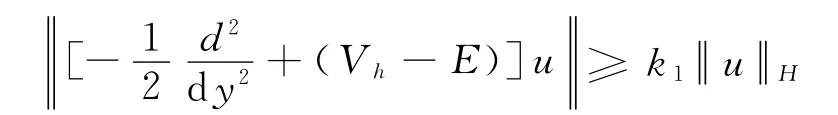
定理2 存在正实数γ,α1,h1,使得当时,有
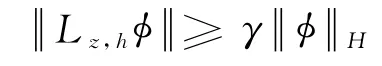
证明 采用文献[11-12]的方法,假设定理结论不成立,则存在收敛于(0,0)的序列(zi,hi)∈R×R+及序列对每个i,有

考虑H中的序列

对每个i,由式(7)及式(9)知则可在H中选出子序列仍记为ψi,使得ψi弱收敛于ψ∞.又(ψi,u′0)=0,故(ψ∞,u′0)=0.
下证ψ∞=0.定义线性算子

对R上的任意有界区间Ω,定义,则
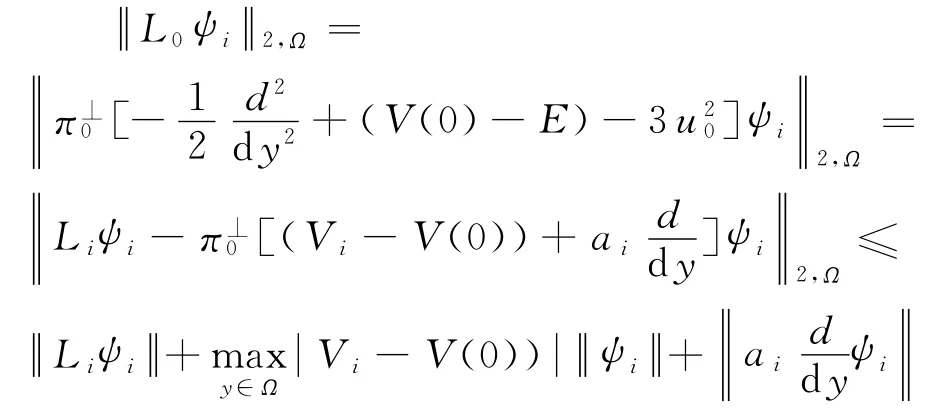

对于Biu,有

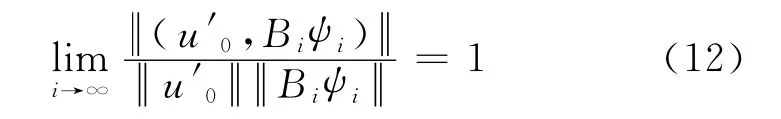
由Hh-E的自共轭性及S′0(u0)u′0=0知

所以

由(Vi-V0)u′0在R上一致收敛于0及的有界性知((Vi-V(0))u′0,ψi)→0(i→∞).由ψi弱收敛于0知由的有界性及ai→0(i→∞),得0(i→∞).所以与式(12)矛盾.定理得证.
2 非线性估计
本部分主要证明,对z∈R和足够小的h>0,存在φz,h∈K⊥z,h,使得

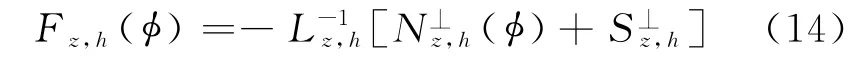
由式(6)可知,式(13)等价于φz,h是Fz,h(φz,h)的不动点.
下证Fz,h(φ)在0的一个适当的小邻域内是一个压缩映射,由定理2知所以还需对作估计.
引理3[1]存在不依赖z和h的正数C,δ,对φ,φ′∈H,当时,有


其 中,v1,k3与h无 关.特 别 地,0((z,h)→(0,0)).
证明 由S0(uz,h)=0 可 得,Sh(uz,h)=(Vh-V(0))uz,h+a(hy)u′z,h.由

及


定理4 存在正常数D,α0,h0,使得对满足的z和h,有唯一的H,使得
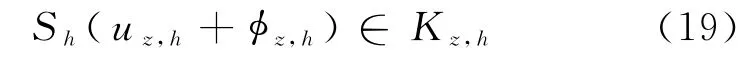
及
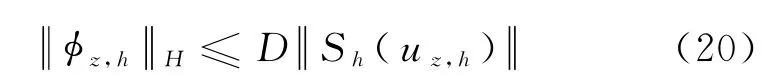
根据定理2,选取满足h0≤h1,α0≤α1的h0,α0,使得时,下证Fz,h(φ)是从的压缩映射,对,易知Fz,h且

即Fz,h(φ)是从到的映射.对于φ,φ′∈,有



3 主要结果的证明
定义函数sh:(-α0,α0)→R为


定理5 函数vh在[-1,1]上一致收敛到v0.
证明 由式(22)得

下面,对e1,e2,e3,e4进行估计.
由于e1= (u′z,h,(Vh-V(0)uz,h)=-(uz,h,V′huz,h)- (uz,h,(Vh-V(0)u′z,h),所以


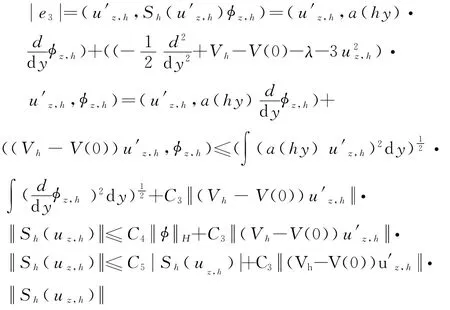
对e4,有


由于v<2,可选取足够小的ε,使得当h→0,所有项趋于0,定理得证.
定理1的证明 由定理5知,对足够小的h>0,vh在(-1,1)上必有一零解.由vh的定义知(Sh(uz,h+φz,h),u′z,h)= 0.由定理4知Sh(uz,h+φz,h)∈Kz,h=span{u′z,h}.综上,当-hz<z<hv时,Sh(uz,h+φz,h)=0,故uz,h+φz,h是式(3)的解.由构造过程知u(y)=v(hy),uz,h且0((z,h)→(0,0)),其中z∈(-h-v,hv),易知uz,h+φz,h在平移量不超过hv-1的u0附近,故方程(2)的解集中在平移量及其微小的u0附近.
[1]Floer A,Weinstein A.Nonspreading wave packets for the cubic Schrödinger equation with a bounded Potential[J].Jour Funct Anal,1986,69(3):397-408.
[2]Oh Y G.Existence of semi-classical bound states for nonlinear Schrödinger equation with potential of the class(V)α[J].Commun Part Diff Eq,1988,13(12):1499-1519.
[3]Oh Y G.Correction to “Existence of Semi-classical bound state of nonlinear Schrödinger equations withpotential of the class(V)α”[J].Commun Part Diff Eq,1989,14(6):833-834.
[4]Oh Y G.On positive multi-lump bound states of nonlinear Schrödinger equations under multiple well potenti-al[J].Commun Math Phys,1990,131(2):223-253.
[5]Oh Y G.Stability of Semi-classical bound states of nonlinear Schrödinger equations with potentials[J].Commun Math Phys,1989,121(1):11-33.
[6]Ding Y H,Szulkin A.Existence and number of solutions for a class of semilinear Schrödinger equations[J].Progress in Nonlinear Differential Equations and Their Applications,2006,66:221-231.
[7]Ding W Y,Ni W M.On the existence of positive entire solutions of a semilinear elliptic equation[J].Arch Rat Mech Anal,1986,91(4):283-308.
[8]Rabinowitz P H.On a class of nonlinear Schrödinger equations[J].Zeits Angew Math Phys,1992,43(2):270-291.
[9]Wang X F.On a concentration of positive bound states of nonlinear Schrödinger equations[J].Commun Math Phys,1993,153(2):223-243.
[10]Weinstein M I.Modulational stability of ground states of nonlinear Schrödinger equations[J].SIAM J Math Anal,1985,16(3):472-491.
[11]Taubes C.Self-dual yang-mills connections on nonself-dual 4-manifolds[J].J Diff Geom,1982,17(1):139-170.
[12]Cantor M.Some problems of global analysis on asymptotically simple manifolds[J].Compositio Math,1979,38(1):3-35.

