需求规模和采购成本双扰动军事物流博弈分析

李建民， 董 鹏， 孟庆霞

（1.武汉大学 系统工程研究所，武汉 430072；2.海军工程大学 管理工程系，武汉 430033；3.荆楚理工学院 经济管理学院，荆门 448000）

生活中经常会遇到诸如需求变化、物价上涨、承制商不能及时或中断供应原材料、自然灾害以及局部战争等突发性事件，不仅会造成舰艇部队物资需求规模变化，也会使军事物资采购中心的采购成本（包括紧急采购增加的运输成本、储存成本和人工成本等）发生变化，这将会直接影响供应链成员的管理决策，进而影响承制商的生产计划，导致整个军事物流系统运作失常或供应链不再协调.对于军事物流系统中的决策者而言，当面临需求规模和采购中心的采购成本同时扰动时，至今还没有一个相对量化的标准.在供应链领域，Xu等［1－2］研究了非线性需求函数和生产成本为凸函数的情形下，需求发生扰动时，由一个供应商和一个零售商构成的供应链扰动管理问题及其协调机制.Yang等［3］考虑了生产函数为凸函数，当生产费用出现变动时，如何用扰动管理的方法修改原来的计划，使系统能够平稳运行且对生产存储造成的影响最小.Tomlin［4］考虑了一个零售商和两个供应商组成的供应链系统，其中一个供应商具有稳定的生产能力，另一个生产不稳定，当供应商的供应出现扰动时，给出了各种情况下的应急策略.Qi等［5］首次对需求扰动下的供应链协调问题进行了分析，在假设零售商面对的市场需求关于零售价格是线性函数的情形下，研究了当市场需求扰动时，供应链如何利用全单位数量折扣契约来协调应对.上述文献考虑的都是单因素发生扰动，比如需求规模、生产成本等，而管理实践中，突发性事件往往造成军事物流系统两个或两个以上因素同时发生扰动，对于这种情况，目前来看文献很少，而且也没有进行系统的研究.本文在此基础上，研究战场形势变化导致军事物流需求规模和采购中心采购成本同时扰动的博弈问题，为决策者进行决策提供支持.

1 军事物流需求规模和采购成本双扰动模型

1.1 问题描述和假设

考虑一个承制商、一个军事物资采购中心和n个舰艇部队构成的供应链系统，它们之间的行为决策可用Stackelberg博弈来描述.在该博弈中采购中心占主导地位，决定着供应价格和供应量，舰艇部队是跟随者；承制商和采购中心基于对舰艇部队的需求预测制定相应的生产计划和采购计划，如图1所示［6－8］.当战场形势急剧变化后，舰艇部队的物资需求规模发生变化，采购中心的采购成本也会变化.模型假设如下：

a.采购中心必须满足舰艇部队的需求量，承制商必须满足军事物资采购中心的采购量.

b.舰艇部队i（i＝1，2，…，n）的实际物资需求量为qi，军事物资供应价格为pi，qi为pi的线性递减函数，设qi＝di－kpi.其中，di＞0为需求规模，k＞0为价格敏感系数（设为常数）.

图1 三级供应链结构模型Fig.1 Three grade supply chain structure mode

c.承制商生产加工该产品的成本C（qi）是其生产数量的凸函数，如生产更多的产品时，需要投入一些员工加班费、通讯费、人员调整费等；若是外购，则外购部分的费用要比自己生产的成本高些.

d.采购中心的单位采购成本为cr，如运输、储存、装卸搬运费用等.

Δdi，Δcr分别表示舰艇部队需求规模和采购中心采购成本的变化量，只有当di＋Δdi＞0，cr＋Δcr＞0时才有意义.设为战场形势变化后舰艇部队i的实际需求量为战场形势没有发生变化时的最优需求量为战场形势变化后的物资供应价格，则

从式（2）可知，当Δqi＞0时采购中心应该采购更多的军事物资来满足新的需求，当Δqi＜0时有剩余物资.设m1表示必须重新购买新材料来增加产量所产生的单位额外成本，m2表示必须将多余材料以低于成本价出售来减少产量而遭致的单位额外成本，且m1，m2均是大于0的，（x）＋＝max｛0，x｝，则供应链渠道i收益函数可表示为

那么，整个供应链系统的收益函数可表示为

a.当Δdi≥kΔcr时，有

b.当Δdi≤kΔcr时，有

证明 假设当Δdi≥kΔcr时，有为式（3）最优解的充要条件是为式（4）的最优解.

当需求和采购成本不变时，供应链渠道i收益为：易验证∏i（qi）为凹函数，当满足下式时，供应链渠道i收益取得最大.

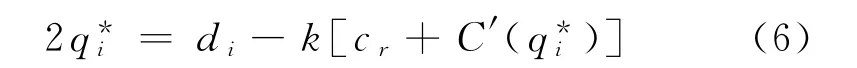
因C（qi）为凸函数，则C″（qi）＞0，C′（qi）为增函数，而又假设于是有C′（）＜0；结合已知条件Δdi≥kΔcr，km2＞0，则这与假设相矛盾，因此假设不成立.故当Δdi≥kΔcr时，有.同理可证引理1中的结论b.

引理1表明，当舰艇部队需求减少而采购中心采购成本增加时，条件Δdi≤kΔcr一定成立，此时承制商应改变生产计划，降低生产水平.当舰艇部队需求增加而采购中心采购成本降低，条件Δdi≥kΔcr一定成立，此时承制商应增加生产水平来满足舰艇部队的需求，采购中心会为了保障供应采购更多的物资.当舰艇部队需求和采购中心采购成本同时增加或同时降低时，承制商应根据引理1给定的条件来判断生产计划，采购中心应根据引理1给定的条件来决定其最优采购量.

1.2 分析与求解

a.当Δdi＝kΔcr时此时供应链渠道i收益函数可表示为求导式（7），可求得满足供应链渠道i收益最大值时的最优解

相应的最优供应价格为

此时供应链渠道i最大收益为

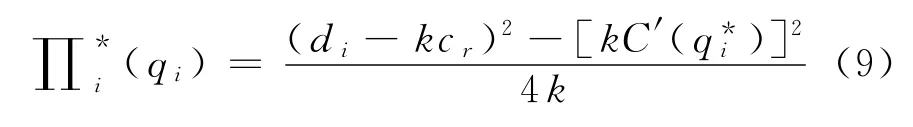
由式（6）和式（8）可知，采购中心的最优订货量与需求规模正相关，与采购成本负相关，与承制商的边际生产成本有关.供应价格与需求规模和采购成本正相关，需求量大，则价格上涨，同时如果采购成本增加，相应的价格也会上涨.在取得收益最大化之后，还要确定供应链收益的合理分配，一般可以通过各种契约和能力约束来实现整体利益的协调［9］.

b.当Δdi＞kΔcr时，有q—＊i＞q＊i，此时供应链渠道i的收益函数可简化为

不考虑约束条件q—＊i＞q＊i，对式（10）进行分析可知道该函数存在唯一的最优解使收益最大，求导可得

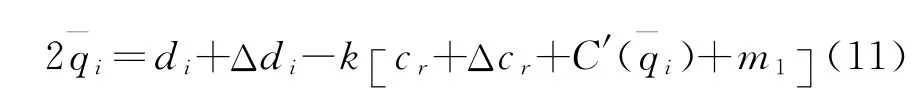
式（11）减式（6）可得由C（qi）为凸函数，可知C′（qi）为增函数，并且有：

情况1 Δdi－kΔcr－km1≥0，当表明能最大化式（10），此时的最优解记为

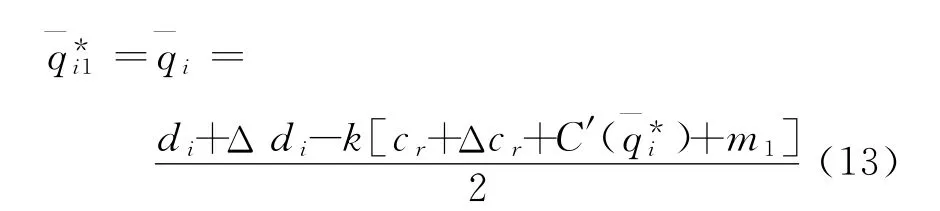
相应的最优供应价格为

此时供应链渠道i的最大收益为

从式（13）～（15）可以看出，当Δdi－kΔcr－km1≥0时，舰艇部队i的最优需求量和最大收益都受到需求规模和采购成本变化量的影响.

情况2 0＜Δdi－kΔcr≤km1，当≤q＊i不满足约束条件≥q＊i时，由凹函数的性质知，在区间，∞］内，供应链渠道i收益函数的最大值为

相应的最优供应价格为

供应链渠道i的整体收益函数为

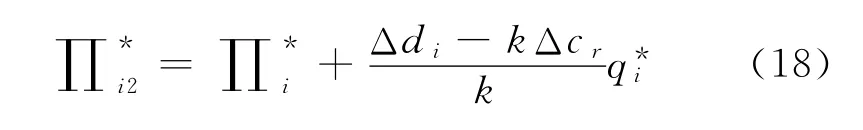
从式（16）～（18）可得，当0＜Δdi－kΔcr≤km1时，虽然需求规模和采购成本同时发生扰动，但是产品计划产量并没有发生变化，仍然是原来的q＊i，只是这时的供应链收益增加了，这是由于形势变化导致供应价格上涨，从而带来的收益增加，可以超过采购成本增加带来的收益的减少；或者是采购成本减少带来的收益的增加，可以超过因需求规模缩小、供应价格下跌而导致收益的减少.采购中心的最优订货量不受需求规模和采购成本的影响，仍保持原计划采购量不变，即承制商在该情形下也不需要改变生产计划.在该情形下，只要需求规模发生变化，其供应价格总是要作出相应的调整，且供应价格与需求规模的变化量正线性相关.由式（18）可知，在该情形下，供应链渠道i收益比原计划收益要大.当Δdi≤kΔcr时，由引理1知，最优订购量小于q＊i，此时供应链渠道i收益函数可表示为

在没有任何约束的条件下，当满足下式（20）时为式（19）的最优解.

式（20）减式（6），可得

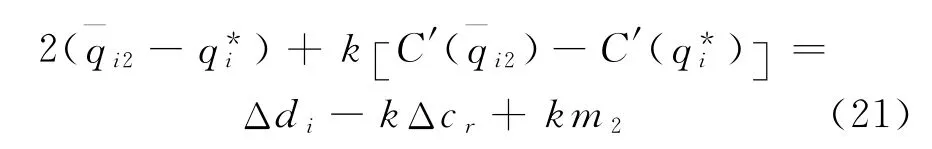
同上，可分两种情形来讨论式（19）满足约束条件q—＊i≤q＊i的最优订货量.

情况3 当－km2≤Δdi－kΔcr≤0时，

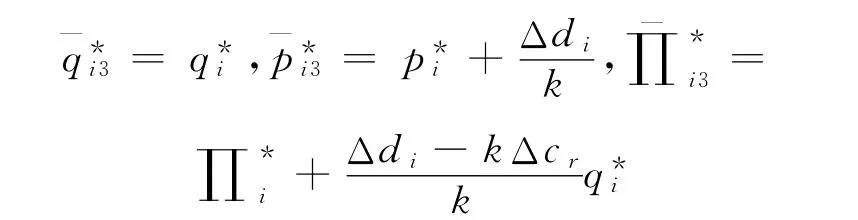
情 况 4 当 Δdi－kΔcr≤ －km2时，

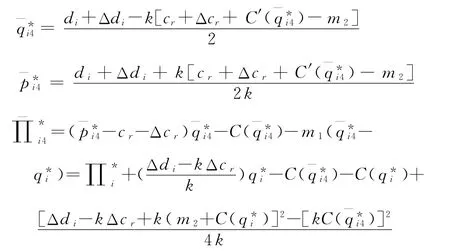
现实中军事物资的供应价格是不可能小于承制商的生产成本和采购中心的采购成本之和的，即对于任意的需求量qi＞0，总有pi－C′（qi）－cr－Δcr＞0，等价于di＋Δdi－k［cr＋Δcr＋C′（qi）］＞0.

1.3 博弈分析

当战场形势发生急剧变化，造成舰艇部队需求规模变化了Δdi，采购中心的采购成本变化了Δcr，且承制商的生产成本是其生产数量的凸函数，为使整体收益达到最大，决策者需要适时调整最优订货量和采购成本.根据扰动的不同变化情况，订购数量和供应价格分别为

决策者应该采取的策略为：在舰艇部队需求规模和采购中心采购成本同时发生扰动的情况下，对原生产计划和采购计划有一定的鲁棒性，当变化比较大时，超出了一定的范围，才会调整计划.当变化比较小（满足－km2≤Δdi－kΔcr≤km1）时，保持原计划不变.此时，只需要通过调整供应价格弥补扰动发生时带来的偏差费用即可，此时供应价格只受需求规模的影响，随着需求规模的增大而增大，而与采购成本无关.而对于供应价格，不管变化大或小，只要需求量发生了变化，则供应价格就要相应地作出调整.需求规模增加，供应价格上涨；需求规模减少，供应价格降低［10－11］.

2 算例分析

用一个简单的例子说明上述结论.当战场形势变化导致di和cr同时扰动时，通过算例计算分析它们对供应链系统、采购中心和承制商收益的影响.设di＝200，cr＝20，k＝4，m1＝5、m2＝5，承制商的生产成本是需求量的凸函数，C（qi）＝q2i，可以根据价格需求关系算出q＊i＝12和p＊i＝47.但实际中往往是需求和采购成本同时增大或同时减小，因此仅对这两种情况进行分析.对扰动情况按上文的情况1～4分类，结果如表1.

表1 di和cr的扰动对军事供应链的影响Tab.1 Effect of diand crdisturbance on military supply chain

从表1中可以看出：

a.当需求和采购成本同时发生同方向的扰动时，在一定的条件下，并不会对原有的生产计划和采购计划产生影响，两者之间存在着一种相互抗衡和制约的作用，即一者变化带来的不利影响可以被另一者变化带来的有利影响抵消或部分抵消，此时供应链的生产计划保持不变，如表1中情况2和情况3的4种扰动情况.在该情形下，只需要适当地调整供应价格即可达到供应链的最优，且此时只有当需求规模发生变化时，才需要调整供应价格，供应价格随需求规模的增大（减少）而上涨（减低）.

b.当需求和采购成本同时发生同方向的扰动时，并且两者之间的关系超过一定的条件，如表1中情况1和情况4的4种扰动情况时，承制商的生产计划和采购中心的采购计划都要随之进行调整，可通过增加订购量且提高供应价格，或者减少订购量且降低供应价格来达到供应链的最优.同时在情况1下，供应链的生产计划必须作出调整，并且供应链的最优生产量、最优价格和最优利润随着需求规模的增大而增大，随着采购成本的增加而增加.

c.从表1还可以看出，如果在需求和采购成本同时发生扰动时，策略不作调整，即使整个供应链的收益为正，承制商和采购中心可能也会因为自己单方面无利可图（得到负的收益）退出供应链，从而使得双方都失去盈利机会.

通过研究还发现，在不同的扰动情形下，供应链的最优订购量、最优供应价格和供应链的最优利润，与采购成本、需求规模及它们的扰动存在着一定的关系.当突发事件导致需求和采购成本同时发生不同方向的扰动，并且两者之间的关系超过一定的条件时，如当采购成本增加和需求减少时，与稳定状态时相比，承制商会通过减少生产来应对突发事件；当采购成本减少和需求增加时，承制商会通过增加生产来应对突发事件，引理1已证明之.

3 结 论

对其动态模型进行分析并得出在舰艇部队需求规模和采购成本同时发生扰动时，原来生产计划和采购计划仍有一定的鲁棒性，变化比较小时，保持原计划不变，若超出一定范围，才会调整计划.计划的改变取决于需求和采购成本两种扰动的综合作用.本文仅对单承制商、单采购中心、多舰艇部队组成的三级供应链进行了研究，后续将考虑多承制商、多采购中心、多舰艇部队时的情形，或者考虑需求函数为非线性需求或随机需求时，研究多种扰动因素对供应链的影响；这些扰动因素之间的关联关系及相互影响、变动的机理也是今后研究的方向.

［1］Xu M，Qi X，Yu G，et al.The demand disruption management problem for a supply chain system with nonlinear demand functions ［J］.Journal of Systems Science and Systems Engineering，2003，12（1）：82－97.

［2］Xu M，Gao X.Supply chain coordination with demand disruption sunder convex production cost function［J］.Wuhan University Journal of Natural Science，2005，10（3）：493－498.

［3］Yang J，Qi X，Yu G.Disruption management in production planning ［R］.Austin：The University of Texas，2005.

［4］Tomlin B.On the value of mitigation and contingency strategies for managing supply chain disruption risks［J］.Management Science，2006，52（5）：639－ 657.

［5］Xia Y，Yang J，Golany B，et al.Real－time disruption management in a two－stage production and inventory system ［J］.IIE Transactions，2004，36（1）：1－15.

［6］吴献金，杨泽寰.成本和需求同时扰动的多零售商供应链协调［J］.湖南大学学报（自然科学版），2010，37（5）：88－92.

［7］罗云金.战时军事物流的博弈分析［D］.南京：南京理工大学，2009.

［8］冯花平.基于多因素扰动的供应链应急协调研究［D］.北京：北京邮电大学，2008.

［9］Huang C C，Yu G，Wang S，et al.Disruption management for supply chain coordination with exponential demand function［J］.Acta Mathematica Scientia，2006，26（4）：655－669.

［10］雷东，高成修，李建斌.需求和生产成本同时扰动时的供应链协调［J］.系统工程理论与实践，2006，26（9）：51－59.

［11］Cachon G P，Lariviere M A.Supply chain coordination with revenue－sharing contract strengths and limitations［J］.Management Science，2005，51（1）：30－44.