基于人力资本视角的世代交叠模型修正
张国民, 陈 进, 梁 丹
(上海理工大学 管理学院,上海 200093)
现代经济增长理论证明,消费(储蓄)和投资的变动对经济增长和经济波动作用巨大,在规范的经济增长模型如Solow-Swan模型、Robinson-Kaldor模型和Romer模型中,决定经济增长的因素无非是物质资本的累聚与配置、人力资本的积累与利用、技术进步与知识增长等,所有这些驱动因素实际上都是经济体中无数消费者(或家庭)及厂商决策的结果.作为经济结构的重要一方,消费者(或家庭)在作出消费决策的时候要考虑哪些因素,新古典经济框架中的效用分析作出了一定的解释,但偏重于如何消费的问题.对消费者是否消费以及使用多少资源进行消费的问题只有Ramsey在他的跨期选择理论中作过一定的阐述.世代交叠模型的提出,为这些问题的解决提供了广阔的思路.但是,经典的世代交叠模型——OLG模型存在着明显的缺陷,在其理论应用和解决实际问题时有一定的局限性,在以往的相关研究中并未及时地对此问题进行解决和修正.本文主要以人力资本理论为基础对经典的世代交叠模型进行全新修正,通过最优均衡分析得出经济运行中更符合实际的模型结果,并利用修正模型框架对经济运行中的消费问题以及人力资本投资、社会保障体系的一般规律等问题进行简要分析.
1 世代交叠理论评述
1.1 世代交叠模型的提出和应用简介
世代交叠模型(OLG模型),又称叠代模型、Diamond模型,该理论建立在跨期选择模型理论的基础上,由Allais和Samuelson在分析美国的养老保障基金的运作模式时首先提出[1].1965年Diamond将Samuelson等人的思想与Solow增长模型进行融合并加以发展,建立了较完整的经典意义的世代交叠模型.Diamond在模型中假设个人的生命具有有限期界,即人们只存活于不变数目的离散时期之中,他把人的生命周期分为青年和老年两个世代阶段.一个世代的青年人与上一世代的老年人在同一时间段内相互重叠同时存在,世代交叠模型的通用名称正是由此而来.OLG模型的精髓在于,个人只具有有限期界——他们只活两个时期而且根据假设他们并不在乎其后代的福利——但是经济却永远持续[2].这样,它就抓住了经济主体“有限期界”的重要特征,为模型中的一系列重要结论提供了必要条件.Blanchard[3]对世代交叠模型进行了进一步的修正,通过假设人们以泊松过程随机死亡,将世代交叠模型在某种程度上扩展到了无限时域,在一个更易于处理的框架中保留了有限期界思想的精华.
世代交叠模型是以微观分析为基础的动态模型,该模型是当代经济学的一个重要理论,在经济学多个学科具有广泛的应用价值,成为许多领域如宏观经济分析、财政学、国际经济学、金融学等的重要分析工具.许多经济学家利用此模型来研究资本积累、利率和消费、储蓄率、政府支出等对均衡产出及均衡产出增长率的影响等问题.例如,OLG模型是货币经济学研究领域经常使用的三大主要模型之一,Wi1liamson曾建立了一个含有逆向选择问题的世代交叠模型来讨论银行货币发行权问题;Bernanke和Gertler利用Diamond模型对RBC(真实商业周期)模型进行改良,构建了金融加速器模型;Tirole和Weil曾运用世代交叠模型证明证券市场投资者理性泡沫存在的可能性,并证明泡沫只可能存在于一个具有动态结构的世代交叠经济体系中;Persson和Tabellini将OLG模型引入财政学,研究了在财政纯粹进行再分配情况下收入分配对经济增长的影响[4-5].
世代交叠理论在社会保障问题研究中的应用最为广泛,是该领域的最主要理论模型之一.国内外许多学者利用该模型分析和解决社保基金运作的相关难题,到目前为止已经取得了丰硕的成果,如规范分析证明:社会养老金的增长取决于人口的增长率和劳动生产率的增长率两个因素;Auerbach和Kotlikoff、Kotlikoff通过实证分析建立了大规模的仿真世代交叠模型[4];国内的柏杰,袁志刚、宋铮,何新华,袁志刚和郑伟等根据我国实际情况,利用国内数据的实证分析[7-10],为我国社会保障理论的发展作出了突出贡献.
1.2 经典世代交叠模型存在的缺陷
虽然几十年来针对OLG模型的研究如火如荼,但是,绝大多数都是将Diamond的经典模型当成一种工具在不同领域展开应用,试图去解决实际问题.只有少数人去发现OLG模型本身固有的缺陷,对Blanchard模型的修正也仅仅是停留在函数形式和计量方式上,仍然沿用Diamond的基本思想.站在Becker等人的人力资本理论视角,可以发现经典的OLG模型的几个疏漏和偏颇,这些一直被广大学者所忽视.这些疏漏和偏颇表现在如下几点:
a.世代交叠模型的精髓就是把人的有限生命期限分成两个阶段,即有工作能力的青年阶段和无工作能力靠以前的储蓄生活的老年阶段.这种思维确实为解决经济学的现实难题提供了一个广阔的视野和非常实用的方法,然而却把人们由出生到参加工作之前的这段青少年时期完全忽略.值得注意的是,这个时期对于人的生命周期来说是至关重要的,人们的个人禀赋在这个阶段进行初始积累,这个阶段生成人的人力资本基本价值,而且,人们在这个时期的消费活动是毫无个人经济依托的,因为,这个时期和人的年老时期一样没有经济收入.那么,个体的这个阶段对资源的消费来源于何处且又如何计量,这个阶段的消费行为对其它阶段产生如何的影响,这些问题在Diamond模型中并未提及.
b.经典的OLG模型主要分析个体在有限期界内的两个人生阶段的消费或储蓄决策问题,即当如何选取一个均衡储蓄率以实现个体效用最大化问题,经济增长中如何选取一个社会整体储蓄率以实现最优经济均衡问题.模型中把个体年轻阶段的经济收入看成一个外生变量或者是劳动力市场供求关系均衡的结果,并未说明这种经济收入的真正来源,更重要的是它是由什么因素决定,这些在经典的OLG模型中未作解释.
c.Diamond在把世代交叠思想融入Solow-Swan模型时并未考虑人力资本这个重要因素,这是可以理解的,OLG模型在20世纪50年代被提出,而人力资本理论却是在60~70年代由Becker等人提出并逐步完善.然而,在这之后的学者在研究OLG模型时却依旧忽略了这个问题,一直像对待制度因素一样把人力资本视作外界给定因素,忽略人们的人力资本投资及利用行为,这显然是不科学的.
d.经典的OLG模型抓住了经济主体的“有限期界”的重要特征,为模型的一系列重要结论提供了必要条件.但是,由于模型涉及到的变量多是外生变量且相互之间关系复杂,这样均衡条件就过于累赘和繁琐,难以进行比较静态分析,经典的OLG模型并未找到一个本质性的且能贯穿于模型始终的关键变量进行研究.
本文的创新在于:利用人力资本这个本质因素对经典的世代交叠模型进行较大范围的修正.本文将个体的生命周期的有限期界划分为三个阶段,人力资本初始投资阶段、人力资本使用和“干中学”阶段、人力资本退出阶段.经济系统在每个时刻都是以上三个阶段并存的,三个阶段相互依存且相互影响,三个阶段所拥有的一切资本投入(包括人能力和物力)创造个体总产出.最重要的是,本文找到了人力资本投资以及人力资本投资回报两个因素变量,并使之贯穿于OLG模型的全过程,大大简化了经典模型的均衡结果和均衡路径,而且可以方便地进行比较静态分析.最后,简要说明修正的OLG模型在分析我国的消费政策以及社会人力资本投资、社会保障等问题中的应用,论证修正模型的理论和现实意义.
2 人力资本修正的世代交叠模型框架
2.1 前提假设
由于本文仅是站在人力资本视角对传统的世代交叠模型的一个修正,因此,分析时仍旧沿用模型原假设,并作部分扬弃与补充.
a.生产技术满足新古典条件,即边际报酬递减且规模报酬不变;经济体系为封闭经济,市场条件为完全竞争,不存在市场失灵和信息不对称等情况;
b.人口变量设为外生给定,即人口以固定比率n增长;社会技术进步设为外生,给定不变的技术增长率β=a(t)/A(t)[9],A(t)为t时期全要素水平,a(t)为t时期全要素增长水平;
c.经济个体无差异,且均属于风险规避类型,本文中的“个体”指一种社会平均.
相对于Solow增长理论,假设中放宽了储蓄率外生给定条件,除此之外的其它假设和Solow模型基本一致,出于模型简化考虑,且本文讨论范围仅局限于微观消费最优问题,并未向宏观经济增长作过多拓展,因此,作如上假设.
2.2 修正的OLG模型的基本框架
2.2.1 有限期界三个阶段的人力资本划分
按照人力资本理论,作为人力资本载体的每个个人皆可被当作一种社会资本对待,人的生命周期之内的生、壮、衰、死完全可以视为这种资本的运动过程.本文将按照这种人力资本的运动过程把人的有限期界划分三个阶段:人力资本初始投资阶段、人力资本使用阶段和人力资本退出阶段.本文中第二阶段即人力资本使用阶段的经济收入是人的生命周期中所有消费的来源,在模型中处于关键地位,所以,在修正的OLG模型中把这个阶段作为当期,用t表示,这样,把第一阶段也称作前期,用t-1表示;同样把第三阶段叫后期,用t+1表示.个体在三个阶段的消费水平设为C0t-1,C1t,C2t+1(0,1,2分别表示三个世代,初始投资阶段的世代这里用0表示).现对三个阶段作一个说明.
人力资本初始投资阶段,即人从出生到参加工作之前的生命时期.在这个阶段,个体还不具备获取稳定经济收入的能力,需要依靠父母或社会资源来实现生存和成长需要.为了便于分析,本文把个体在这个阶段的消费C0t-1视为一种社会借贷,并且需要其在下期利用自己的经济收入对这种借贷的本息进行偿还.这种假设是十分合理的,因为,即使本期的消费来自于无私的父母的提供,个体也要以另一种方式偿还的,比如养老等.从另一个角度,完全可以把这种“社会借贷”视为一种人力资本投资行为,因为,个体在这个阶段的社会借贷帮他完成了原始的人力资本存量的积累和提升,如身体机能的完善、教育的投入、知识和阅历的增长等,这种借贷投入在未来会为其产生收益.我们会很容易意识到,这些人力资本的初始投资是相当关键的,这是个体在以后各个阶段消费来源的主要基础,个体在下一个阶段的工作情况和收入水平一般意义上完全取决于这个阶段的人力资本投资水平(设为K0)的高低.
人力资本使用阶段,即个体从参加工作到失去工作能力以致退休的生命时期.在这个阶段,个体利用前期的投资形成的人力资本存量寻找合适的工作,以获取稳定持久的经济收入.这种经济收入的多少一般要取决于以下几个基本因素:前期人力资本投资额、人力资本投资的社会平均收益率和个体在“干中学”的经验积累即技术进步.由于本文研究的是社会一般情况,无数个体“干中学”中的人力资本积累的平均水平无限接近于社会技术进步水平,本文直接用社会进步水平来替代这种一般意义的个体经验积累情况.关于这些经济收入的使用,本文将其分为三个部分:当期消费部分C1t,对前期借贷消费的偿还和补偿部分C0t-1,以某种方式(存款或者社保基金)留足的储蓄以备无经济收入的下期消费部分C2t+1.可以很明显地看到,个体当期的经济决策将是修正模型的关键,个体当期的决策总和将决定整个经济增长和社会保障以及人力资本投入政策,是政府制定经济发展决策的标准.
人力资本退出阶段,即个体从退休到去世的生命时期.在这个阶段,个体没有工作收入,靠上一个阶段的储蓄度过余生,个体在这个时期生活条件的好坏取决于其前期的储蓄决策和政府的社会保障体系情况.
经济体中上述三个世代阶段是同时存在的,并且相互交叠、相互影响.这是符合世代交叠理论的思想精髓的.在上述分析的基础上,本文构建了三个世代的消费函数
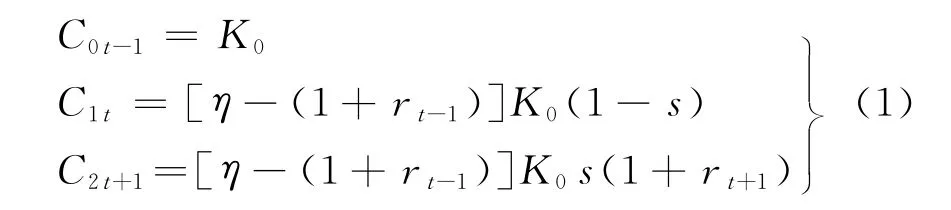
式中,r为不同时期的社会利率水平;s为社会均衡储蓄率;η=η(α,β),为初期人力资本投资K的回报率.
人力资本收益率η=η(α,β)中,α为社会平均人力资本回报率,β为技术增长率,满足η(α,β)>0,η′(α,β)>0,η″(α,β)>0.
2.2.2 效用函数的构建
由于个体在三个时期(t-1,t,t+1)内生存,三个阶段的消费水平分别为C0t-1、C1t、C2t+1,则取个体效用总函数为

式中,p为效用的时间贴现率,又称时间偏好率,p>0.p可以理解为消费效用的贬值率,p>0,反映了人们总是看重近期的效用,对较晚得到的效用评价较低.这便是西方的观念里的“父母式的自私”.
式(2)表示消费者的总效用是按照比率p贴现后各个世代阶段的效用现值总和.贴现率p的设计是很有必要的,没有p,U是无穷大的量,无法用效用最大化来作消费决策分析.
本文中效用函数u(C)将使用当今前沿经济增长模型分析中大多采用的CRRA(常相对风险规避)形式[3-5],即

式中,θ为相对风险规避系数,等于边际效用对消费的弹性的绝对值是CRRA效用函数的曲率.
可以证明,在CRRA效用函数下,θ与消费者效用的跨期替代弹性σ成反比[10-11].一般情况下,消费者各个时期效用的跨期替代弹性σ或者相对风险规避系数θ都是恒定不变的常数.θ值的经济意义在于它决定了消费者转换消费的偏好.θ值越大,消费者就越偏好于有波动的消费流,其消费的变动就大[10-11];θ值越小,消费就越偏好于相对平稳的消费流.
本文进行世代交叠模型修正分析中之所以采用CRRA效用函数的形式,是因为该效用函数能够保证人们的消费模式存在一定的延续性和可预测的规律性,使得对人们经济行为的分析成为可能[9].
很明显,CRRA效用函数满足新古典条件,即u′(C)>0、u″(C)<0,且符合消费行为的一般规律.由此得出个体在人生有限期界内的效用总函数为
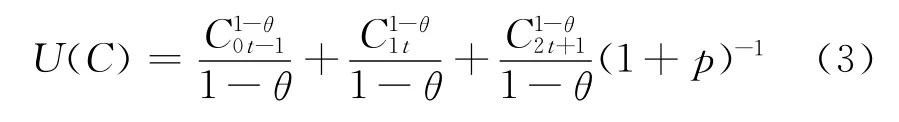
2.2.3 修正模型的基本框架
通过以上分析可以得到人力资本修正的世代交叠模型的基本框架
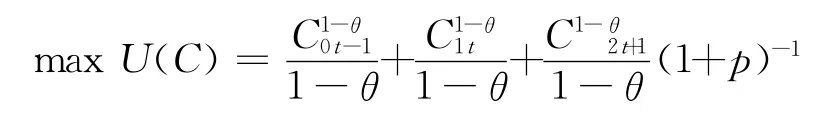

3 修正模型的均衡分析
本文继续使用Ramsey跨期选择模型的思路,通过求解个体在有限期界内的总效用最大化来求解修正的OLG模型的最优均衡解.
修正模型基本框架中的3个约束条件可以合并为

这样修正的模型框架就变为

利用拉格朗日方法求极值
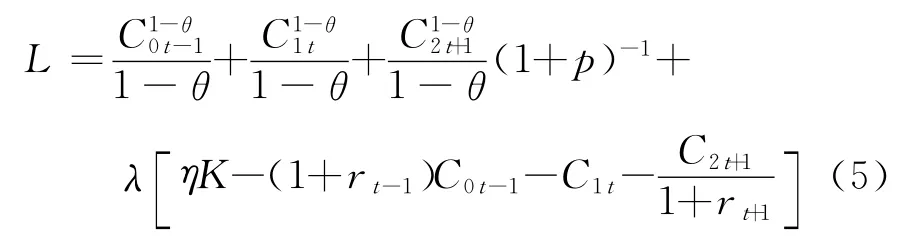
式(5)的一阶条件为
由式(3)整理得到

3.1 求解均衡消费率和储蓄率
由于储蓄率s和消费率c的关系为s+c=1.因此,可以通过求出当期消费率来计算储蓄率.当期消费率可通过c=C1t/ηK求得.利用式(4)和式(7)计算得出均衡结果为


可见,当期消费率和储蓄率都是社会平均利率r的函数,由利率r决定,其变动取决于r的波动情况.在这里完成了储蓄率s的内生,这是对新古典经济学模型中关于利率外生的一个完美修正.在Solow-Swan模型中储蓄率s是外生的,这样假定主要基于两点考虑,即在一定时期内储蓄率s比较稳定,这样做可以简化模型分析.但是,消费(储蓄)率其实是变动的,尤其在长期时它们与经济增长存在着明显的互动作用,一个经济体系的稳态、收敛性和内生性都与消费(储蓄)率有密切关联;或者说取决于它们的变化.所以,应将消费(储蓄)率在分析框架中内生化.Ramsey模型和世代交叠模型都将s作为内生变量整合进了模型分析当中,增强了模型的解析力.收入又是由产出、资产存量水平决定的,所以,将消费(储蓄)率内生化的基本要求是考察在不同的产出、资产存量水平下的消费行为,从而推导出它们的内生关系.
式(9)是模型的最优均衡结果,s(r)函数的确定是修正模型研究的最重要部分,是基于世代交叠模型对经济增长理论研究的关键.储蓄率是资本路径的决定因素,新古典经济增长理论中将储蓄率视为关键变量.值得注意的是,在本文的修正模型中,不同代际人的最优储蓄率(消费率)是不同的,并且由于个体经济收入是一个关于人力资本投资及其回报率、经验积累和技术进步的动态函数,由此决定的储蓄亦是不稳定的动态变量.这样,经济稳态并不唯一,表现出很大的不确定性,这也正式世代交叠模型与其它新古典模型的重大差别之处.动态的储蓄率也正是OLG模型解释“动态无效率”的突破口.
政府在制定经济政策时应充分考虑这种经济最优均衡所决定的储蓄率函数以及其动态性,否则,可能造成政策失效甚至适得其反的结果,导致经济秩序紊乱和不必要的资源浪费.
3.2 求解最优消费增长率
由于消费增长率v由公式v=C2t+1/C1t-1决定,利用公式

可以求得

式(10)表明,人力资本修正的OLG模型的理性个体若要实现人生总效用的最大化,必须使其消费增长率遵守该条件.
3.3 社会平均人力资本回报率的求证
由式(4)和式(7)经整理得到人力资本社会平均收益(回报)率η(α).由于技术进步率β在本文设为外生给定的一个常值,为了简化模型和说明问题,这里不作考虑.

由此可以看出,人力资本社会回报率亦是社会利率r的函数,r是这种回报率α的决定变量,这是符合常理的,资本之所以为资本,就在于它对收益率的追求,而对于资本运作好坏的基本评价方法就是与机会成本相对比,人力资本也不例外.社会利率r无疑是最佳的机会成本核算依据,这便是本文修正OLG模型的科学性所在.
4 修正的世代交叠模型应用展望
消费或者储蓄问题直接关系到经济运行的各个方面,从微观层面的企业投资、个人理财决策、教育和养老问题到宏观层面的就业研究、通货膨胀、社会保障、经济增长,都与消费息息相关[1,9].近几年来,学术界对刺激消费、扩大总需求的研究非常重视.2008年的金融风暴对我国经济的冲击不亚于美国、日本、西欧,这次经济危机的实质亦是通货紧缩,而通货紧缩的主要成因之一就是总需求不足,这点在我国的体现比较明显,因此,对消费的研究不仅具有理论意义,而且具有重大的现实意义.利用修正世代交叠模型分析框架,可以构建OLG经济的消费模型,在数据分析的基础上给模型的各项基本参数赋值,通过实证分析测算世代交叠模型下居民最优消费增长速度和消费(储蓄)比率,研究消费者行为的一般规律,为政府的经济政策出台提供必要的借鉴.
在世代交叠模型中,不同代际的人有不同的消费倾向和不同的财富水平,这是该模型独具特色之处,理性的个体在每个时期的经济决策都要对整个生命的有限期界内预期和续存作出考虑.其中,人力资本投资和保障性储蓄是最基本和必须的经济行为,社会人力资本投资制度和社会保障体系的建设,无疑会改变个体消费者(或家庭)所面临的预算约束以及厂商的决策函数,影响个体的消费行为、人力资本决策、企业的劳动力需求决策及工资支付制度、工会与企业之间的议价博弈的变化等,从而对经济增长产生巨大的影响.本文中修正的OLG模型证明,社会性的人力资本投资是极其重要的,决定着个体有限期界内的生活质量以及社会经济增长的韧性和潜力;政府的社会保障不仅仅是一种福利供给,更是经济发展的调节剂.但是,不论是社会人力资本投资还是社会保障体系,其合理构建必须符合经济体的一般规律,要符合适当的比率和力度.对于这些问题,本文的分析具有一定的借鉴意义.本文的研究为人力资本投资和社会保障制度的建设打下一定的理论基础,研究结论为政府的相关经济政策提供了必要的依据.
另外,世代交叠模型根基于市场经济假设,与个体消费选择相关的资本与劳动收入、税后可支配收入、消费与储蓄等家庭决策行为应该是完全市场化的.修正模型在其它经济形式下的适用性有待进一步研究.
[1]Samuelson P A.An exact consumption Loan model of interest with or without the social contrivance of money [J].Journal of Political Economy,1958,66(3):124-131.
[2]Diamond P A.National debt in a neoclassic growth model[J].American Economic Review,1965,55(5):344-357.
[3]布兰查德·奥利维尔.宏观经济学(高级教程)[M].刘树成,译.北京:经济科学出版社,1998.
[4]巴罗·罗伯特.经济增长[M].何晖,译.北京:中国社会科学出版社,2000.
[5]罗默·戴维.高级宏观经济学[M].苏剑,译.北京:北京商务印书馆,1999.
[6]Auerbach A J,Kotlikoff L J,Hagemann R P,et al.Economic dynamics of an aging population:The case of four OECD countries [J].OECD Economic Studies,1989,12(5):277-292.
[7]袁志刚,宋铮.城镇居民消费行为变异与我国经济增长 [J].经济研究,1999(11):20-28.
[8]袁志刚,宋铮.人口年龄结构、养老保险制度与最优储蓄率 [J].经济研究,2000(11):39-46.
[9]何新华.养老保险体制改革成本的最小化研究 [J].世界经济,2001(2):3-12.
[10]郑伟.养老保险制度选择的经济福利比较分析 [J].经济科学,2002(3):74-83.
[11]Barro R J,Becker G S.Fertility choice in a model of economic growth[J].Econometrica,1989,57(2):481-501.

