有强Cwrpp Rees根的本原wrpp半群
高振林, 李海沙
(上海理工大学 理学院,上海 200093)
1 相关概念和问题
首先,给出渉及到的已有概念.
定义1[2]半群S上的Green关系L和R定义为

定义2[3]半群S上的Green**-关系L**和R**定义为
(a,b)∈L**当且仅当对∀x,y∈S1(ax,ay)∈R⇔(bx,by)∈R
(a,b)∈R**当且仅当对∀x,y∈S1(xa,ya)∈L⇔(xb,yb)∈L令
J**(a)=其中,J(x)是由x生成的主理想;
L**(a)=∪{L(x)|x∈L**(a)}其中,L(x)是由x生成的主理想.
称J**(a)(L**(a))为由元a生成的**_主理想(**_主左理想),用它引进的J**-关系为
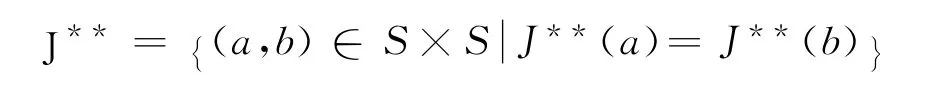
定义3[4]半群S的非零幂等元e称为本原幂等元,若e是非零幂等元集中关于自然序的极小元.
定义4[4]如果半群S的所有幂等元都是本原的,则称S是本原半群.
定义5[4]设I为S的非零左理想,则称其为S的0-极小左理想,如果对S的任意非零左理想A⊆I,有A=I并且I含零元.
定义6[1]称S为wrpp半群,如果S满足下列条件:
a.S的每个L**-类至少含有S的一个幂等元;
b.对∀a∈S,∀e∈E()有a=ae,其中E()为的幂等元集.
称wrpp半群S为Cwrpp半群,若E(S)⊆C(S),其中E(S)是S的幂等元集,C(S)是S的中心.称wrpp半群S为充足的,若对∀a∈S,∃|a+∈E()使得a=a+a.称充足wrpp半群S为左Cwrpp半群,若E(S)是左正则带且L**是同余.本文引进以下概念:
定义7 半群S上的同余ρ称为S上的Cwrpp同余.如果S/ρ是 Cwrpp半群;令ρ是S上(Cwrpp)同余,如果存在S的子集I满足S=I∪C,且C同构于S/ρ则称I是S的(Cwrpp)ρ-集,这时将ρ记作ρI.
定义8S为半群,如果S不包含任何Cwrpp同余,那么定义S的Cwrpp根同余是泛关系S×S,且称S是Cwrpp根半群;如果S至少包含任何一个Cwrpp同余,那么定义S上的Cwrpp根同余是所有Cwrpp同余ρα(α∈ω)的交集,记作ρcr,即
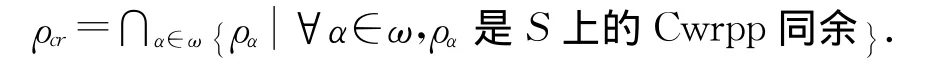
如果ρcr也有ρcr-集,记为N(S),所以ρcr=ρN(S).称N(S)为S的Cwrpp根;称半群S的Cwrpp根同余ρcr是强Cwrpp根,若ρcr仍是S的Cwrpp同余,且N(S)存在.此时

定义9[5]假设N,T*是不相交半群,T有零元0,T=T*∪{}0称半群S是由T关于N的一个(理想)扩张,如果N是S的一个理想,且S/N≅T.
定义10 称I为半群S的(0-)**-左(右)理想,若I为S的左(右)理想且对
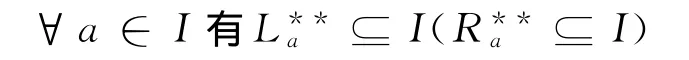
这里()是包含α∈S的L**(R**)-类;称S的子集I为S的(0-)**-理想,若I既为S的**-左理想又为S的**-右理想;称S的子集I为理想(0-)**-左(右)理想,如果I既是理想又是(0-)**-左(右)理想.
定义11 有零元的半群S称为左0-**-单的,如果S的理想**-左理想只有S或{}0且S2≠{}0;无零元的半群S*称为左**-单的,如果它没有真理想**-左理想.
定义12 设S是wrpp半群,如果ρN(S)是强的且N(S)是理想,那么称S为有强Cwrpp Rees根的wrpp半群;若S还是本原半群,则称其为有强Cwrpp Rees根的本原wrpp半群.
引理1[4]一个0-单半群是完全0-单半群,当且仅当它至少有一个本原幂等元.
引理2[4]设e为半群S的本原幂等元,则Se是S的一个0-极小左理想.
引理3[4]S是单0-半群,L是S的0-极小左理想,那么L\}是S中极小非零L-类.
定理1[4]若S是有零元的本原正则半群,那么S是完全0-单半群的0-直并.由定义11易得以下结论.
引理4 在有零元的半群S上,下列命题成立:
a.S*是左**-单的,当且仅当J**是S上的泛关系;
b.S是左0-**-单的,当且仅当S2≠且,L\}是S的仅有J**-类.
引理5[4]以下结论成立:
a.(R**-关系)L**-关系为任意半群S上的(左同余)右同余且在S上有下列式子成立:
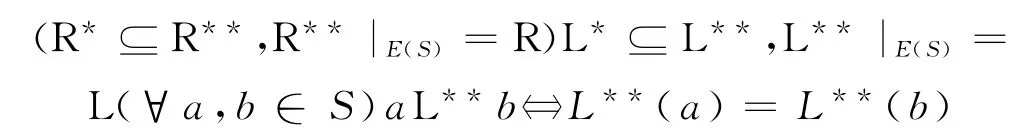
b.设U是半群S的子半群,则LU⊆LS∩(U×U);RU⊆RS∩(U×U).
引理6 下列命题成立:
a.[3]有零元的Cwrpp半群C有半格分解表示
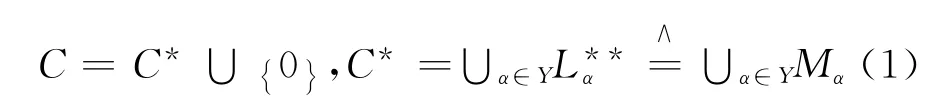
其中,(α∈Y)是左R-可消幺半群.
b.[1]在有零元的左Cwrpp半群S上,L**=J**是S上半格同余.
引理7 设S为有强Cwrpp Rees根的wrpp半群,则
a.N(S)是wrpp半群;
b.N(S)=∩α∈ω{Iα|对于∀α∈w,Iα是S的wrpp子半群,Cwrpp理想};
c.设a∈S,则有幂等元且J**(a)是S的wrpp理想**-左理想.
证明 因S为有强Cwrpp Rees根的wrpp半群,所以
a.设a∈N(S)⊆S,因S是wrpp半群,故有e∈E(),使得a=ae.因N(S)是S的理想,e∈E()⊆⊆L**(a)⊆N(S),故∃e∈E(N(S))使得aL**N(S),a=ae成立.故N(S)为wrpp半群.
b. 由 定 义 8 知N(S) = ∩α∈ω是S的因N(S)是S的理想,故N(S)是S的最小Cwrpp理想.而命题b右边的集合显然也是S的最小Cwrpp理想,故它必等于N(S).
c.由于S是wrpp半群,所以∃e∈E(S)使得于是再证J**(a)是S的wrpp理想**-左理想:由于J**(a)是由元a生成的**-主理想,故J**(a)既是S的理想又是其**-左理想,故J**(a)是S的理想**-左理想.又由a的证明过程可知,J**(a)是wrpp半群.综上,J**(a)是S的 wrpp理想**-左理想.
基于以上定义和结论,我们应用有零元的Cwrpp半群C有半格分解表示 (即式 (1)),强Cwrpp Rees根性质和本原性质,用理想扩张的手段来刻画有强Cwrpp Rees根的本原wrpp半群的结构特征.
2 有强Cwrpp Rees根的wrpp半群的性质
以下若不特别声明,S总表示有强Cwrpp Rees根的wrpp半群.
性质1 设S是本原的,则
a.S的仼一子半群是本原的;
b.对0≠e∈E(S),a∈S,aL**e当且仅当a≠0且a∈Se.
证明 结论b的证明类似于文献[6]中推论3.2的证明,这里省略,只证结论a.
设T≤S,S是本原的,即∀e∈E(S),e在S上是本原的,由于E(T)上自然序所以∀e∈E(T),e在T上也是本原的,故T是本原的.
性质2 设a∈S,若J**(a)是非零主理想**-左理想集合中极小元,则J**(a)=∪{}0.
证明 显然⊆J**(a).反之,设0≠x∈J**(a),显然J**(x)⊆J**(a),由J**(a)是非零主理想**-左理想集合中的极小元和引理7推出J**(x)=J**(a),即x∈.因此J**(a)=∪{}0.
性质3 下列结论成立:
a.对∀a∈S,J**(a)=∪{Je|e∈E)};
b.对∀a∈S,L**(a)=∪{Le|e∈E)};
c.S的理想**-左(右)理想I可表为I=∪e∈E(I)J**(e).
证明S是有强Cwrpp Rees根的wrpp半群,所以
a.由J**(a)定义:∀e∈E(),有Je⊆(a),故∪{Je|e∈E)}⊆J**(a),另一方面,设0≠x∈J**(a),由引理5、引理7,得

b.显然∪{Le|e∈E()}⊆L**(a).另一方面,设0≠x∈L**(a),S是wrpp半群,故∃e∈E)使得
c.设T=∪e∈E(I)J**(e),可证T是S的理想.为此先证T为S的子半群
∀a,b∈T∃e,f∈E(I)使得a∈J**(e),b∈J**(f)而J**(e)是S的理想,所以有ab∈J**(e)⊆T.故T为S的子半群.又∀a∈T,∃f∈E(I)使得a∈J**(f),由于J**(f)为S的理想,故有∀s∈S,as∈J**(f)⊆T,sa∈J**(f)⊆T,故T为S的理想.
再证T是S的**-左理想:对a∈T,存在f∈E(I),使得a∈J**(f)由于J**(f)是S的理想**-左理想,则⊆J**(f),当然有⊆T,所以T是S的**-左理想.综上,T是S的理想**-左理想.
最后证I=T成立:由于I是S的理想**-左理想,对∀e∈E(I),J**(e)⊆I,所以有T⊆I;设a∈I则存在e∈E(I)使得a∈,即有=.又T是S的理想**-左理想,故有=⊆T,因此a∈T,所以I⊆T.综上,I=T.
性质4 对0≠e∈E(S),以下各条件等价:
(a)S1e是非零幂等元生成主左理想集合中的极小元;
(b)e是本原幂等元;
(c)S1e是0-极小**-左理想;
(d)S1eS1是非零幂等元生成主理想集合中的极小元;
(e)S1eS1是左0-**-单的.
证明 (a)⇒(c)由非零幂等元生成主**-左理想集合被非零幂等元生成主左理想集合包含,即得该结论成立.
(c)⇒(a)设S1e是0-极小**-左理想.若有f∈E(S)使得S1f⊆S1e,往证S1f也是0-**-左理想:首先S1f是S的左理想,其次由于S是wrpp半群,那么∀a∈S1f⊆S有h∈E(),=,a=ah∈S1h从而S1f⊆S1h同理可证S1h⊆S1f故S1h=S1f于是有==⊆S1f,由定义10,S1f是0-**-左理想.由S1e是0-极小**-左理想得S1f=S1e.从而结论(a)成立.
(b)⇒(a)设e是S的本原幂等元,如果0≠f∈E(S),S1f⊆S1e那么f=fe,因此efef=eff=ef,efe=ef=eef,即ef∈E(S),ef≤e.从而ef=0或ef=e.若ef=0,则efe=ef=0从而推得.f=f2=fefe=f·0=0这与0≠f∈E(S)矛盾.因此ef=e,S1f=S1e.即(a)成立.
(a)⇒(b)如果(a)成立,设f∈E(S)使得f≤e,那么ef=fe=f,S1f⊆S1e.因为S1e是非零幂等元生成主左理想集合中的极小元,所以S1f=S1e.故e∈S1f,e=ef=f成立.即(b)成立.
(b)⇒(d)设e是本原幂等元,假定,对0≠f∈E(S)有S1fS1⊆S1eS1,则有u,v∈S使得f=uev.取元素g=evfue,则g有性质
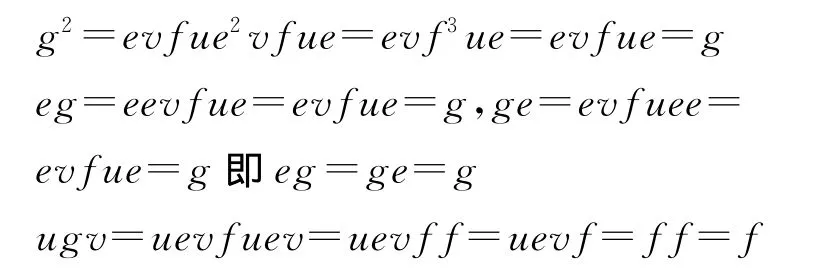
因此g是非零幂等元且g≤e.由于e是本原的,有g=e.因为f=ugv,g=evfue,所以S1fS1=S1gS1=S1eS1.因此(d)成立.
(d)⇒(b)假定对某个0≠f∈E(S),f≤e成立.由ef=fe=f推 出S1f⊆S1e,从 而,S1fS1⊆S1eS1.由于S1eS1是非零幂等元生成主理想集合中的极小元,因此S1fS1=S1eS1,从而对e∈S1有S1fe=S1ee所以S1f=S1e从而f=e.(b)成立.
(d)⇒(e)显然(S1eS1)2≠{}0,设{}0≠A是S1eS1的理想**-左理想,下证A=S1eS1.由性质3知,在S1eS1上,将A表示为A=∪f∈E(A)J**(f).因A≠{0},由 A的表示,故E(A)≠{0},取0≠f∈E(A),则J(f)=S1fS1⊆A⊆S1eS1,由S1eS1是非零幂等元生成主理想集合中的极小元得,A=S1fS1=S1eS1,由定义11知S1eS1是左0-**-单的.
(e)⇒(d)设S1eS1是左0-**-单的,则S1eS1的理想**-左理想只有{}0和S1eS1,因此,由非零幂等元生成的主理想**-左理想集合中只有S1eS1.假定对0≠f∈E(S)有S1fS1⊆S1eS1,则S1fS1是S1eS1的另-个非零理想**-左理想,这与S1eS1是左0-**-单的矛盾,即(d)成立.
性质5S是由它的某个Cwrpp子半群C关于Cwrpp根N(S)理想扩张,得到
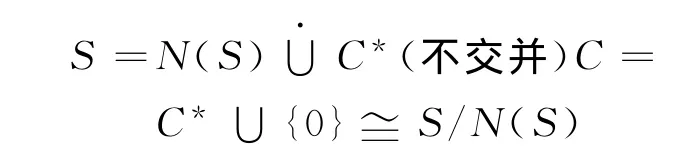
且当S是本原半群时,有
a.C*有依赖于本原半格Y的分解式(1);
b.N(S)是S的理想**-左理想且有不交并表示

其中,J**(e)(∀e∈∩α∈wE(Iα))是S的左0-**-单子半群.
证明 由定义11和定义12知,只要证当S是本原半群时结论a,b成立.
a.由引理6知,C*有半格分解式(1),由于S是本原的,由性质1知,C*也是本原的,即∀e∈是本原的,故Y为本原半格,因此C*有依赖于本原半格的分解式(1).
b.先证N(S)是S的理想**-左理想,这只要证N(S)是S的**-左理想:设a∈N(S),由引理5知,N(S)是S的理想得⊆L**(a)⊆N(S),即N(S)是S的**-左理想.
再证式(2)成立:由于N(S)是S的理想**-左理想,由性质3知,N(S)可表示为N(S)=∪e∈E(N(S))J**(e),由引理7知,N(S)=∩α∈ωIα,所以故式(2)成立.

最后证J**(e)(∀e∈∩α∈wE(Iα))是S的左0-**-单子半群:设{0}≠A是J**(e)的-个非零理想**-左理想,由引理7,J**(e)是wrpp半群,故
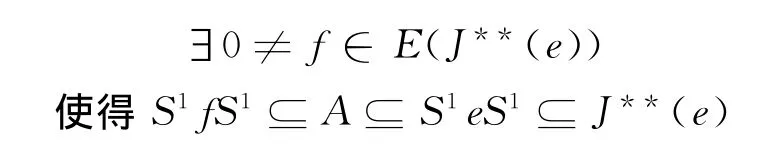
应用性质4(b)⇒(d)的证明得e=f∈A.因{0}≠A是J**(e)的-个非零理想**-左理想,由e=f∈A得A=J**(e),即J**(e)是左0-**-单的.
3 有强Cwrpp Rees根的本原wrpp半群的结构特征
下面给出有强Cwrpp Rees根的本原wrpp半群的一个结构特征,并用实例说明这类半群具有其独特意义.
定理2 对于有强Cwrpp Rees根的wrpp半群S,以下条件等价:
(a)S是本原的;
(b)S是Cwrpp半群C关于N(S)的理想扩张,其中N(S)和C满足条件:
(1)N(S)是本原wrpp左0-**-单子半群的0-直并;
(2)C是本原wrpp左0-**-单子半群的0-直并.
(c)S是本原wrpp左0-**-单子半群的0-直并.
证明 (a)⇒(b)由性质5,设本原半群S是它的某个Cwrpp子半群C关于N(S)的理想扩张.只需证(1)(2)成立,现证(1).由性质5知,J**(e)是左0-**-单的(∀e∈∩α∈wE(Iα)).下证N(S)是J**(e)(∀e∈∩α∈wE(Iα))的0-直并.由于对∀e,f∈∩α∈wE(Iα)
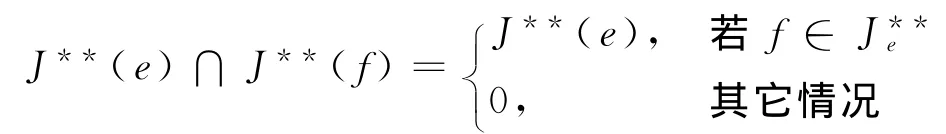
设x∈且y∈,那么. 因为
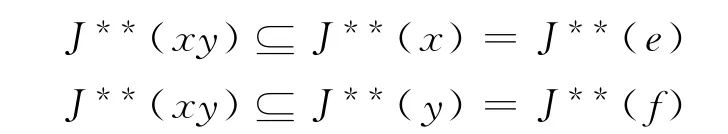
得J**(xy){}=0或J**(xy)=J**(e),J**(xy){}=0或J**(xy)=J**(f).因此
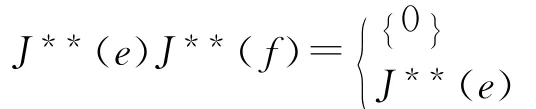
综上知,条件(1)成立.由性质5,用相同方法可证(2)成立.
(b)⇒(c)由(1)(2)和性质5式(2)知
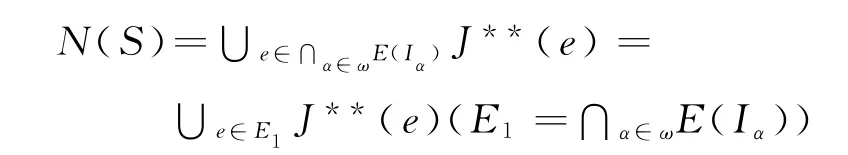
由引理6,令E2={1α}α∈Y这里1α(α∈Y)为左R-可消幺半群=(α∈Y)的幺元.令¯E=E1∪E2,由S=N(S)知.于是

由结论(b)和以下亊实:
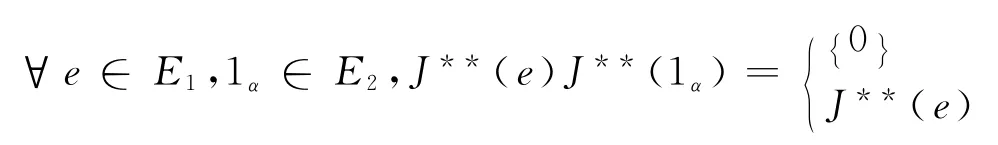
即使(c)成立.
(c)⇒(a)由题设条件不妨设S=∪e∈¯EJ**(e)是本原wrpp左0-**-单子半群J**(e)的0-直并(e∈是幂等元),由性质4,e∈是J**(e)的本原幂等元,且对 ∀h∈J**(e),h是J**(e)的本原幂等元.往证结论(a)成立.
对∀f∈E(S),设有α∈使得f∈J**(α),只要证明f是S的本原幂等元即可,假设有0≠h∈E(S)使得h≤f,∃β∈使得h∈J**(β),分以下情形进行:
a.若J**(α)≠J**(β)则J**(α)∩J**(β)=Φ,由题设条件得h=fh=hf=0,不可.
b.若J**(α)=J**(β)则f,h∈J**(α),f,h是J**(e)的本原幂等元,从而在J**(α)上,由h≤f推得h=f.
综上所述,知f是S的本原幂等元,从而结论(a)成立.
最后给出有强Cwrpp Rees根的本原wrpp半群的例子以说明其独特意义.
例1 设C*是无零元的本原Cwrpp半群,C=C*∪{}0,C的半格分解由(引理6中)式(1)给出,则易见Y是本原半格.由引理6,设左Cwrpp半群N(见文献[4])有依赖于本原半格Y的半格分解N=∪α∈Y.则有以下结论:
a.易知,E(N)包含由Y决定的子带E1为
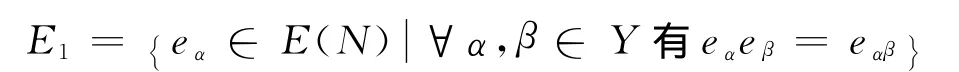
b.N是本原半群:事实上∀e∈E(N)∃α∈Y使得e∈E(),若有f∈E(N),f≤e则f∈E)(β∈Y),由于Y是本原半格,故f=e,即e是本原的,所以N是本原半群.
c.N和C满足条件(1)(2):首先是本原wrpp左0-**-单子半群,下证N和C是的0-直并:事实上,由于Y是本原半格,所以∀α,β∈Y有α≤nβ⇔α=β,从而有
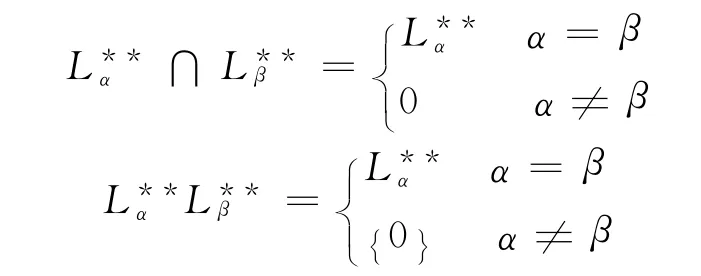
所以,N和C是本原wrpp左0-**-单子半群的0-直并.令

定义 从C*到N的映射

可证θ是一个局部同态映射[6]:∀x,y∈C*,则存在α,β∈Y使得x∈Mα,y∈Mβ,不妨设x=xα,y=yβ则存在zαβ∈Mαβ,使得

在S上定义如下运算"°":
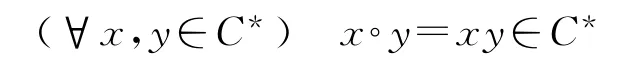
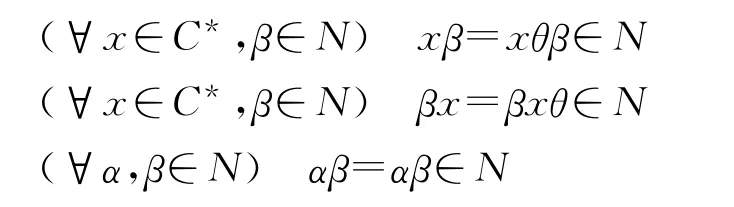
则易验证S成为C关于N的理想扩张半群.由定理2知,S是有强Cwrpp Rees根的本原wrpp半群.由于故S不是文献[1]中的SBCRW-半群.说明这类半群有其独特意义.
[1]Du L,Shum K P.On left Cwrpp semigroups[J].Semigroup Forum,2003,67:373-387.
[2]Fountain J B.Abundant semigroups[J].ProcLondon Math Soc,1982,44(3):103-129.
[3]Tang X D.On a theorem of Cwrpp semigroup[J].Communications in Algebra,1997,25:1499-1504.
[4]Howie J M.An introduction to semigroup theory[M].London:Academic Press,1976.
[5]Clifford A H,Preston G B.The algebraic theory of semigroups[M].Providence:American Mathematical Society,1961.
[6]Fountain J B.Adequate semigroups[J].Proceedings of the Edinburgh MathematicalSociety,1979,22(1):113-125.

