船用双相不锈钢焊接结构疲劳性能研究

王智祥，王正伦，张 鑫

（重庆交通大学 a.船舶工程中心；b.机电与汽车工程学院，重庆 400074）

1 引 言

双相不锈钢（DSS）具有强度高、低温韧性好、抗疲劳强度高和对应力腐蚀不敏感等优良特性[1-3]。近年来，双相不锈钢焊接件和焊接结构的应用尤其广泛，比如在化学品船建造、各类管道、海洋平台等行业。在特种船舶制造方面，使用双相不锈钢建造的化学品船防腐能力非常强，后期维护费用低，船舶安全性得以大大提高[4]。船体是一种典型的焊接结构，焊接质量和性能直接影响到船舶的安全性能[5]。本文以我国化学品船舶建造中首次使用国产不锈钢带来的技术难题为研究背景，以重庆市重大科技攻关项目“特种船舶焊接技术研究（CSTC2008AB3033）”为支撑，采用疲劳实验和有限元模拟相结合的方法对船用双相不锈钢焊接结构的疲劳性能进行了相关研究。研究结果对掌握船舶焊接结构的疲劳特性，揭示双相不锈钢的疲劳的本质，防止特种化学品船生命周期内失效事故的突然发生，有着重要的理论意义和实用价值。

2 疲劳裂纹扩展速率实验

2.1 实验材料及设备

本次实验所用双相不锈钢产自太原钢铁厂，由国营川东造船厂提供，该厂是我国首次运用国产双相不锈钢来建造5500 t化学品船舶的制造商。为了研究该材料的疲劳裂纹扩展速率，首先按照GB/T 6398-2000《金属材料疲劳裂纹扩展速率试验方法》[6]（后简称《方法》）的规范要求从母材上直接截取试板并加工成规格:100 mm×200 mm×10 mm。其次，通过船厂提供的材料数据、加工工艺以及大量实际生产经验，实验将试板加工为V型坡口并进行对焊。再次，从焊后的试板的焊缝、热影响区及母材上取材，并按照《方法》的要求加工为图1的SE（B）试样。最后，将试样的表面磨光，并从切口顶端沿切口延伸线每隔1 mm画刻度线，以方便之后疲劳裂纹长度的测量。实验在PLG-200高频疲劳实验机上进行，该型号高频实验机最大负荷量程为500 kN,由微机控制，试样则采用FWDH8标准三点弯曲夹具进行装夹（见图2）。

图1 试样尺寸Fig.1 Size of sample

图2 疲劳实验现场图Fig.2 Fatigue test site pictures

2.2 实验过程

为了研究不同应力对材料疲劳裂纹扩展速率的影响情况，实验中选取了应力比R为0.1，0.3和0.6三种应力比工况进行实验，最大载荷选取17 kN，加载频率控制在101.5～108 Hz，如表1所示。

实验采用了《方法》中推荐的方法，具体操作如下:在实验过程中逐一记录裂纹长度ai（i=1,2,3,…,n）及相应的载荷循环次数Ni（i=1,2,3,…,n），其中裂纹长度ai（i=1,2,3,…,n）采用JC-10型20倍放大显微镜结合刻度线进行测量，载荷循环次数Ni由实验机自动记录，记录值随时标在坐标纸上。当裂纹扩展到24～28 mm时停止实验。

表1 疲劳实验方案Tab.1 Fatigue test program

2.3 实验数据处理及分析

参考《方法》的内容，扩展速率da/dN由一组对应的裂纹长度a和循环数N值采用多点递增法求得。应力强度因子ΔK则按公式（1）求得:

式中:α=a/W（a为裂纹长度，mm），ΔP为实验加载范围，N；B、W分别为试件宽度和试件高度，mm。

分别在应力比R为0.1，0.3和0.6三种工况下进行实验并随时记录数据，然后采用《方法》推荐的七点回归分析法对3组数据进行线性回归分析，得到相应的材料系数C和n，其结果如表2所示。

表2 三种应力比下疲劳裂纹扩展速率回归分析结果Tab.2 Regression analysis of fatigue crack behavior in three stress ratio

由表2可见，当R=0.6时，材料常数C、n在一个量级上，说明母材、热影响区以及焊缝的疲劳裂纹扩展速率基本是一致的，处于同一个水平上。而当R=0.1，0.3时，材料常数C、n出现明显的差别。尤其常数C的变化，已经跨越了几个量级。这说明了当R=0.1，0.3时，3个位置的疲劳裂纹扩展速率有着较明显的差别，并且随着应力比的减小，这种差别越明显。而观察相关系数，数值都基本处于0.92附近，说明数据的线性关系较好[7]。把所有的da/dN数据进行整理，得到焊接件不同部位的疲劳扩展速率（如图 3）。

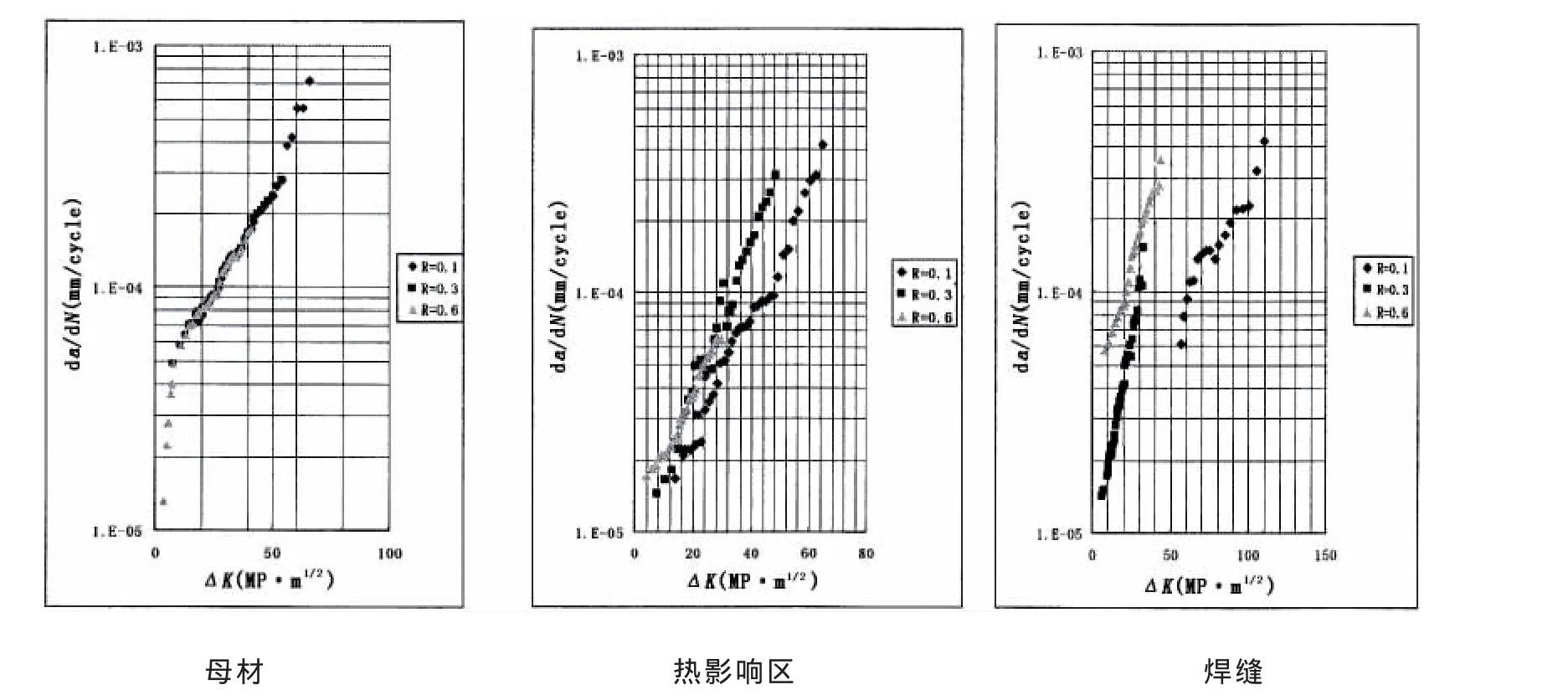
图3 母材、热影响区、焊缝的疲劳扩展速率Fig.3 Fatigue crack growth rate of BM,HAZ and WM

进一步整理，可以得到母材、热影响区以及焊缝各自在不同应力比下da/dN与△K的回归方程，具体如下:

由（2）-（4）式可以看出，船用双相不锈钢母材随着应力比的增加，疲劳裂纹扩展的速率随之增加，这与疲劳裂纹扩展的基本理论[8]相一致，但增加量并不明显，基本维持在一个相同的速率水平上。如△K为20和40的时候，三个应力比下的da/dN的取值几乎是相同的。同时，这也说明双相不锈钢母材的裂纹扩展速率对应力比的变化并不敏感，母材的疲劳裂纹在应力发生变化时扩展仍会维持在一个比较稳定的状态，不会有过大的起伏。

由（5）-（7）式可以看出，随着应力比的提高，热影响区的疲劳裂纹扩展速率同样随着应力比的提高而增加，但其速率分布点已经不处于同一个分布区域，所以其疲劳裂纹扩展速率变化更加显著。如△K为18，R=0.3时的da/dN比R=0.1时的da/dN略大，而当R=0.6时的da/dN已是R=0.1时的2倍多。因此，热影响区的疲劳裂纹扩展速率对应力比的变化具有一定的敏感度，并且高于母材。

由（8）-（10）式可以看出，焊缝处的疲劳裂纹扩展速率也是随着应力比的增加而增加，且幅度更大，它与热影响区的规律更为相似；焊缝处的疲劳裂纹扩展速率对应力比的变化有较强的敏感度，并且在母材与热影响区之上。

纵观（2）-（10）式，在同一应力比的前提下，船用双相不锈钢焊接街头不同部位的疲劳裂纹扩展速率也是不相同的。比较R=0.1时，母材、热影响区和焊缝的疲劳裂纹扩展速率相比母材的速率最大，焊缝的速率最小。如△K取30时，母材的da/dN约为0.0001，而热影响区和焊缝的da/dN分别为0.00004和0.00001。而当R=0.3和R=0.6时，也有类似的结果。其抗疲劳比较，母材的抗疲劳裂纹扩展能力最弱，焊缝最强，热影响区居于二者之间。

3 有限元模拟与实验结果对比分析

本文进一步运用有限元分析软件对该材料的裂纹扩展进行了模拟，并结合损伤模型的理论，用Fortran编写计算裂纹扩展速率的后处理程序，最终得到模拟结果，并将实验结果与模拟结果进行了对比分析。

3.1 有限元模拟

利用有限元分析软件有关断裂力学的分析计算的相关功能，结合实验中试件的实际情况以及预制裂纹附近的相关区域，建立了船用双相不锈钢疲劳裂纹扩展数值模拟的二维裂纹模型，如图4所示。

图4 二维裂纹模型图Fig.4 Two-dimensional crack model

图5 裂纹尖端处网络划分Fig.5 Network division at the crack tip

在有限元建模过程中，几何模型转换为有限元模型时，大量的计算结果表明，网格的细化对结果有较大影响，网格越细结果越接近实验结果，但是网格细化到一定程度后对疲劳裂纹扩展速率的影响非常小，并且计算过程中裂纹尖端网格加密区的网格边长越小，在有限元模拟求解过程中发现结果的收敛性越差[9]。在实际操作时，通过反复的调试并逐步对网格进行细化，考虑到裂纹尖端的奇异性，并且要最大可能地提高计算的精度，在这里最终选取了PLANE82奇异单元来对模型进行网络划分，模型网格划分后如图5所示。为了模拟船用双相不锈钢循环加载过程，参照实际实验过程选定加载频率为104 Hz，最大载荷为17 kN，而应力比分别定为0.1，0.3和0.6，即载荷下降到10%，30%和60%。

3.2 有限元模拟结果

通过以上模型建立，网格划分，载荷确定等步骤，经有限元分析软件对疲劳裂纹扩展进行计算，可以得到裂纹尖端处每个节点的坐标和每一步的应力应变值的相关信息。

图6 R=0.1:加载初期的总应力图Fig.6 R=0.1:the total stress diagram at initial load

图7 R=0.1:加载初期的总应变图Fig.7 R=0.1:the total strain diagram at initial load

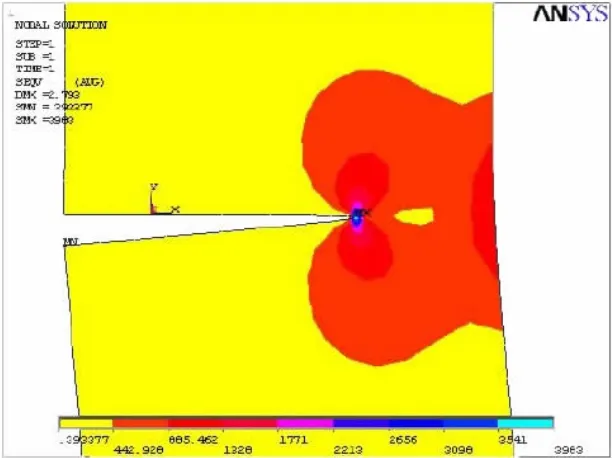
图8 R=0.1:裂纹扩展到23.3 mm时的应力图Fig.8 R=0.1:stress diagram of the crack when 23.3 mm

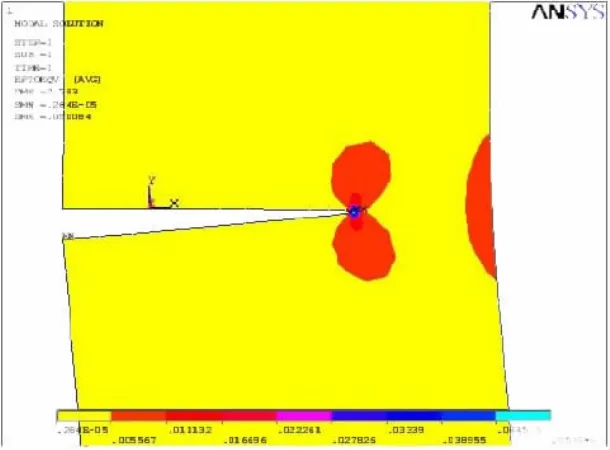
图9 R=0.1:裂纹扩展到23.3 mm时的应变图Fig.9 R=0.1:strain diagram of the crack when 23.3 mm

图6、图7为开始以应力比0.1加载时试样总应力与应变图。由图8可以看出，整个模型的应力最大值发生在裂纹尖端处。图8和图9为在应力比为0.1，加载至试件裂纹扩展长度为23.3 mm时的应力应变图。此外，经过有限元软件计算后同时会生成模型中的结点坐标信息和载荷步信息，将这些数据进行保存，利用Fortran语言编写出一个疲劳裂纹扩展速率相关参数的后处理程序，绘制出模拟数据的da/dN－△K的模拟关系曲线，如图10所示。

为了与实验数据拟合得到的疲劳裂纹扩展速率Paris公式进行比较，可以将有限元模拟过程中产生的数据直接应用数学绘图软件Origin进行数值拟合，便可得到有限元模拟的近似公式:

3.3 疲劳裂纹扩展有限元模拟结果与实验结果对比分析

将不同应力比下的实验与模拟的da/dN－△K的关系曲线绘制出，如图11。可以看出，在相同应力比条件下模拟与实验的曲线趋势基本相同，这说明本文所用模拟方法较为成功，在工程设计中采用数值模拟来计算、绘制船用双相不锈钢的疲劳性能曲线是可行的。将有限元模拟所得的材料常数C和n与相应的实验数据进行对比分析，其具体数值如表3中所示。

图10 有限元模拟计算获得的da/dN-△K曲线Fig.10 The da/dN-△K curve by finite element simulation

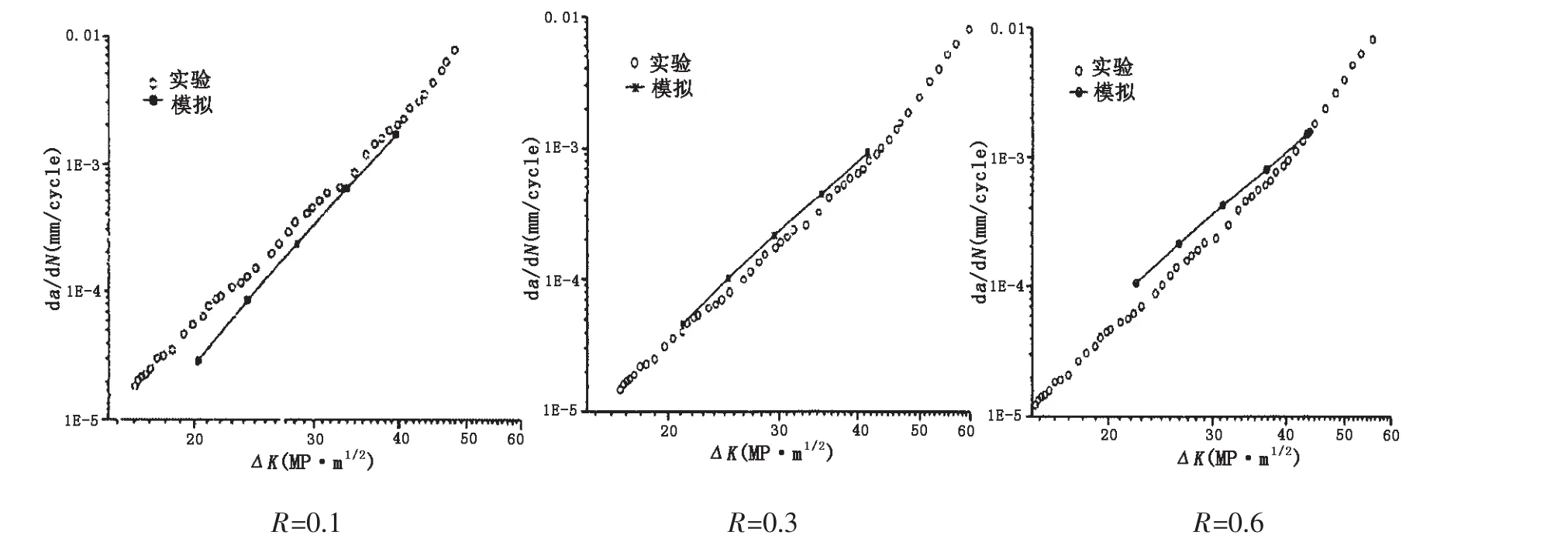
图11 实验与模拟的da/dN-△K曲线Fig.11 The da/dN-△K curves of experiment and simulate

表3 有限元模拟数据与实验数据比较Tab.3 comparison between finite element simulation data and experimental data

从上表中的比较结果可以看出，实验方法与有限元方法所拟合的Paris公式的系数C和n值有一定误差，但相较之前关于低碳钢、合金钢、304不锈钢等材料的研究[10-12]，系数C的水平已从50%至70%的误差大大减小到20%左右。因此用本文所介绍的有限元方法和计算疲劳裂纹扩展的数据处理程序以是可行的。

4 结 论

本文采用标准试样，在PLG-200高频疲劳实验机上分别对焊接试件的母材、热影响区以及焊缝的疲劳裂纹扩展速率等材料的疲劳性能进行了实验研究。通过有限元分析软件对船用双相不锈钢母材的疲劳裂纹扩展进行了进一步的数值模拟，分别绘制了实验结果和模拟结果的da/dN和△K的关系曲线，可得出以下结论:船用双相不锈钢焊缝及周边区域不同部位的疲劳裂纹扩展速率da/dN与应力强因子△K之间变化规律类似于经典力学中的Paris公式。通过实验数据可知，焊缝裂纹扩展速率最低，抗疲劳裂纹扩展能力最高；母材疲劳裂纹扩展速率最高，抗疲劳裂纹扩展能力最差；热影响区介于二者之间，表明川东造船厂所采用的焊接工艺是可行的。由实验所得到的回归方程表明，焊缝处疲劳裂纹扩展的速率对应力比的敏感度最大，热影响区次之，母材最小。本课题组进行的疲劳裂纹扩展实验证明了本文所采用的有限元模拟方法是可行的，这对船用双相不锈钢的疲劳性能在工程中的应用提供了理论基础，具有较大的实用价值。

[1]张建勋,李为卫.2205双相不锈钢的焊接性研究综述[J].焊管,2005,28(5):6-8.Zhang Jianxun,Li Weiwei.Research on welding of duplex stainless steel 2205[J].Welded Pipe and Tube,2005,28(5):6-8.

[2]Walker E K.Effects of environments and complex load history on fatigue life[J].ASTM STP,1997,462:1-12.

[3]Notten G,Charles J,Van Nassau L.Duplex stainless steels[J].The Netherlands,1997(21):9-115.

[4]任 剑,周兆乾.双相不锈钢焊接在造船实践中的应用[J].船海工程,2002(5):15-17.Ren Jian,Zhou Zhaoqian.Duplex stainless steels in shipbuilding practice[J].Ship and Ocean Engineering,2002(5):15-17.

[5]李良碧,潘广善,万正权.高强钢锥柱结合壳焊接残余应力的数值模拟和试验研究[J].船舶力学,2010(10):1143-1150.Li Liangbi,Pan Guangshan,Wan Zhengquan.Numerical simulation and experiments study of welding residual stress of the cone-cylinder pressure hull of high tensile strength steel[J].Journal of Ship Mechanics,2010,14(10):1143-1150.

[6]GB6398-2000金属材料疲劳裂纹扩展速率试验方法[S].北京:国家标准局,2000.The test method of metal fatigue crack growth rate[S].Beijing:National Bureau of Standards,2000.

[7]杨化仁.焊接结构疲劳强度理论[M].沈阳:东北大学出版社,2002:104.Yang Huaren.Welded structure fatigue strength theory[M].Shenyang:Northeastern University Press,2002:104.

[8]钱 怡,崔维成.变幅载荷下疲劳裂纹扩展规律试验研究综述[J].船舶力学,2010,14(5):556-565.Qian Yi,Cui Weicheng.An overview on experimental investigation on variable amplitude fatigue crack growth rule[J].Journal of Ship Mechanics,2010,14(5):556-565.

[9]孙文婷,万正权.对接焊残余应力的有限元分析[J].船舶力学,2007,11(1):94-101.Sun Wenting,Wan Zhengquan.Finite element analysis of butt-welding residual stresses[J].Journal of Ship Mechanics,2007,11(1):94-101.

[10]屠立群,刘宝剑,蔡东海.基于ANSYS的16MnR钢疲劳裂纹扩展分析[J].轻工机械,2010,28(3):44-47.Tu Liqun,Liu Baojian,Cai Donghai.Analysis of fatigue crack growth of 16MnR steel with ANSYS software[J].Light Industry Machinery,2010,28(3):44-47.

[11]Badji R,Belkessa B,Maza H,et al.Effect of post weld heat treatment on microstructure and mechanical properties of welded 2205 duplex stainless steel[J].Materials Science Forum,2004(1):467-470.

[12]邱昌贤,崔维成,田常录.循环压应力下的耐压结构疲劳裂纹扩展分析[J].船舶力学,2010,14(4):409-415.Qiu Changxian,Cui Weicheng,Tian Changlu.Fatigue crack propagation analysis for pressure hull under cyclic compression[J].Journal of Ship Mechanics,2010,14(4):409-415.

[13]周太全,陈鸿天.具初始裂纹钢桥梁焊接构件疲劳裂纹扩展和疲劳寿命计算[J].船舶力学,2009,13(1):91-99.Zhou Taiquan,Tommy Chan Hung Tin.Fatigue crack growth and fatigue life evaluation for welded steel bridge members with initial crack[J].Journal of Ship Mechanics,2009,13(1):91-99.