浮筏系统隔振性能的功率流评价指标

许树浩，桂洪斌

（1中国船舶科学研究中心，江苏 无锡 214082；2哈尔滨工业大学（威海），山东 威海 264209）

1 引 言

潜艇在低速航行时，影响其隐蔽性和探测能力的辐射噪声和自噪声主要是机械噪声。机械噪声是指舰船上的各种机械的振动，通过船体向水中辐射而形成的噪声。其噪声性质以线谱为最明显特征，处于低频段，因为传得较远，成为舰船的目标特征信号。抑制机械设备振动所引起的辐射噪声，主要采用隔振措施，即使用刚度比较小的支撑系统支撑设备，从而隔离振动，并吸收振动能量。浮筏隔振系统具有稳定性高、筏体质量开销少，在多台设备共存的情况下，设备布置灵活等优点。

力传递率一般作为隔振效果的理论预测依据，但由于其不易测量，因此在工程实践中常采用振级落差来评定实际系统的隔振效果。单一的力传递率反映的仅是动态力的传递关系，未能考虑到基础对于传递力的响应，而振级落差则不能反映系统的力传递特性，忽略了振源设备信息。

振动的传递主要是能量的传递，从能量角度研究振动问题更能反映问题的本质。功率流作为一个反映能量的物理量，它既包含了力和速度的幅值大小也包含了两者之间的相位关系，给出了振动传递的一个绝对度量的物理量。对于隔振系统进行的功率流分析可以清楚地表明每一个支撑点或每一台设备对于基础的能量输入，可以指导隔振系统的设计。

功率流研究方法根据系统动力特性分析手段的不同，形成了不同特点的功率流方法。基于导纳原理的功率流法是当前主要的功率流研究手段，主要针对少数简单结构来作理论上的定性研究。Goyder和White在文献[1]中研究了单层和双层隔振系统中功率流的传播机理，建立了隔振系统传递分析的导纳功率流表达形式。文献[2-3]采用了典型的导纳功率流法对一个安装在柔性基础上的多支承隔振系统进行了分析，以振动功率流控制的观点研究了系统的动态特性。基于有限元的功率流法具有较广泛的适用性，大多数复杂结构都可以建模应用有限元分析法进行分析，因此在工程实际中具有广泛的运用。文献[4]从有限元动力方程推导出发，给出了结点频域复数力的表达式，进而给出基于有限元动力分析的功率流计算方法。文献[5]采用子结构改进有限元功率流计算方法，计算精度基本不变但计算效率得到了较大提高。

本文对一个实际筏体结构进行有限元频率响应分析，采用随频率变化的弹簧阻尼器模拟隔振器。在得到弹簧阻尼器两端的速度响应后，从隔振器阻抗方程计算得到隔振器两端的受力值，进而代入功率流方程得到系统的输入、输出功率流值。

2 基本理论

若记f（t）为作用于结构某点处的外力瞬时值，而V（t）为该点的速度响应瞬时值（如图 1），则输入该结构的功率瞬时值为:

对于实际的振动结构的功率流研究往往是取其在一段时间（对于周期振动就是振动的最小正周期）内的平均功率，这种时均功率比瞬时功率更能反映外部激励注入结构的能量强度。按时间平均的功率称为振动功率流，即

若激振力F（t）和响应V（t）均为简谐变化量，即

图1 简单结构振动功率流Fig.1 The vibration power flow of a simple structure

令

由（9）式可以知道，功率流的计算除了计算点处的响应外，还需要知道沿计算点切开时该点在振动中受到的力向量。通过有限元频率响应可以求得复杂结构任意结点上的响应，而隔振系统的功率流输出点（隔振器与基座连接端）所受的力向量可以通过隔振器机械阻抗方程求解。隔振器阻抗方程为

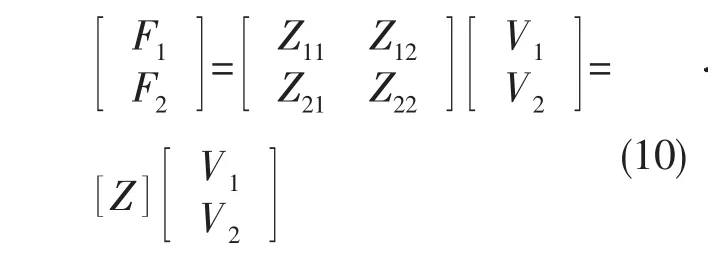
图2 隔振器装置两端力和响应示意图Fig.2 The forces and responses of the isolator ends

将（10）式代入功率流表达式（9）中，得到输入出功率流为:

式中，PIn为隔振器上端输入功率流，V1*为V1的共轭复数。得到输出功率流为:

式中，POut为隔振器下端输出入功率流，V2*为V2的共轭复数。

对于（12）式中的V1、V2可以通过有限元频率响应分析求解。

3 浮筏隔振系统

针对浮筏隔振系统，建立有限元模型，如图3所示。有限元模型中同时考虑了壳体结构的影响，外层壳体厚度为0.03 m，基座面板厚度为0.015 m。材料弹性模量E=2.1×1011Pa，泊松比μ=0.3，结构阻尼η=0.001，密度 ρ=7600 kg/m3。

浮筏模型如图 4所示，筏体上布置三个模拟设备的质量块（见表 1），每个质量块下面布置4个上层隔振器，总共12个。筏体下层布置下层隔振器，总共4个。筏体上面板和下底板厚度为0.005 mm、中竖板厚度为0.003 mm。筏体板材料同壳体和基座面板材料。

图3 浮筏隔振系统有限元模型Fig.3 The FEM model of the float raft isolation system

图4 浮筏有限元模型Fig.4 The FEM model of float raft

表1 筏体上层质量块属性Tab.1 The property of the masses on the float raft

3.1 浮筏隔振系统频率响应分析

对浮筏隔振系统作直接积分法频率响应求解，从1 Hz到200 Hz，分析频率步长取1 Hz。计算得到各节点上的加速度响应值后，将隔振系统上层隔振器上端结点的加速度响应算术平均值作为系统输入加速度响应值，将隔振系统下层隔振器下端结点的加速度响应算数平均值作为系统输出加速度响应值，如图 5。

图5 浮筏隔振系统加速度响应Fig.5 The acceleration response of the float raft isolation system

加速度响应振级落差定义为:

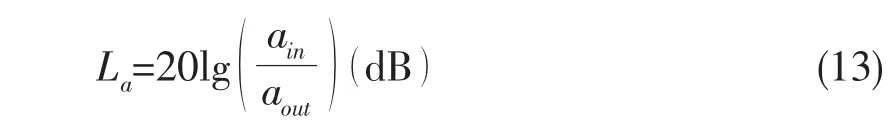
加速度响应振级落差见图6。

3.2 浮筏隔振系统功率流分析

将对浮筏隔振系统进行的频率响应分析中得到的结点速度响应代入（11）、（12）式中可以得到各隔振器的输入、输出功率流值。取隔振系统上层隔振器的输入功率流算数平均值作为系统的输入功率流，取隔振系统下层隔振器的输出功率流算数平均值作为系统的输出功率流，见图7。

功率流振级落差定义为:

图6 浮筏隔振系统加速度响应振级落差Fig.6 The acceleration damping of the float raft isolation system

功率流振级落差见图8。

3.3 结果分析

隔振系统输入输出加速度响应（图5）和功率流响应（图7）反映的都是隔振系统输入输出响应的对比，只是评价标准不同，对比两者可以发现:

（a）两者的峰值的个数相同，峰所在的频率位置相同，基本的曲线趋势也相同。

（b） 加速度响应图（图 5）在 20 Hz和 70 Hz附近频率点上出现了响应被放大的现象，而在功率流响应图（图7）上相应的频率点没有出现这个现象。这是因为在这个频率上虽然加速度响应被放大了，但是功率流的大小在隔振前后是减小的。筏体下层隔振器下端结点（即隔振后的点）的加速度响应大于隔振系统中上层的点（即隔振前的点）是有可能的，但是功率流作为一种能量度量值，只要隔振系统存在阻尼，它总是减小的。

（c）隔振系统功率流响应反映的是振动能量大小的情况，图7说明低频段是系统能量输出的重要通道，应该加强对低频段功率流的输出控制。图5中的隔振系统加速度响应不能反映低频段是系统振动输出的重要通道的这一特点。

在隔振系统加速度响应振级落差图6和隔振系统功率流振级落差图8中可以发现:

（d）功率流振级落差图曲线和加速度振级落差图曲线在趋势上是一致的。

图7 浮筏隔振系统功率流Fig.7 The power flow of the float raft isolation system

图8 浮筏隔振系统功率流振级落差Fig.8 The power flow damping of the float raft isolation system

4 结 论

本文建立了浮筏隔振系统的有限元模型，采用刚度为常数、阻尼随频率变化的Bush单元来模拟实际的5-200 Hz的隔振器的垂向机械阻抗特性。通过有限元频率响应计算得到了浮筏隔振系统的结点响应信息，在此基础上采用隔振器机械阻抗方程求得隔振器两端的受力值，进而代入功率流表达式得到了系统的输入输出功率流。对系统输入输出加速度响应和功率流响应的对比分析可以看到，采用功率流来评价隔振系统的优劣更能反映隔振系统的实际隔振效果。功率流隔振效果更加客观地评价了一个隔振系统的优劣程度。采用功率流作为隔振系统隔振效果的评价标准是合适的，而且在某些方面要优于采用单一的加速度（速度）响应作为评价标准的评价体系。

[1]Goyder H G D,White R G.Vibration power plow from machine into built-up structures,Part III:Power flow through isolation systems[J].Journal of Sound and Vibration,1980,68(1):97-117.

[2]孙玲玲,宋孔杰.柴油机多支承隔振系统的功率流特性[J].内燃机学报,2003,21(4):249-252.

[3]张 峰,俞孟萨,许树浩,等.浮筏隔振系统功率流传递的矢量四端网络参数方法[J].中国造船,2010,51(4):118-126.

[4]伍先俊,朱石坚.基于有限元的功率流计算及隔振系统优化设计技术研究[J].船舶力学,2005,9(4):138-145.Wu Xianjun,Zhu Shijian.Calculation technique of vibration power flow based on finite element analysis and its application in the isolation system optimization[J].Journal of Ship Mechanics,2005,9(4):138-145.

[5]伍先俊,朱石坚.组件功率流计算法和iSIGHT环境下隔振系统优化设计[J].船舶力学,2006,10(2):138-145.Wu Xianjun,Zhu Shijian.Vibration power flow calculation based component modal technique and isolation system optimization using iSIGHT[J].Journal of Ship Mechanics,2006,10(2):138-145.