基座结构形式对艇体振动特性的影响研究

梁德利 ， 计 方 ， 叶 曦

（1北京临近空间飞行器系统工程研究所，北京 100076；2中国舰船研究院，北京 1001923 哈尔滨工程大学 船舶工程学院，哈尔滨 150001）

1 引 言

目前，在研究圆柱壳振动声辐射特性时，很少考虑壳体的内部结构对其振动声辐射的影响。但在实际工程问题中，壳体内部都不可避免地存在某些结构，如基座、横纵舱壁等[1-2]。其中动力设备一般都安装在基座上，动力设备的振动首先将振动传递给基座，然后通过基座将振动传递给其他结构，而壳内基座都是由各种形式的连接结构串联或者并联组合而成。不同的连接结构对振动波的传递是不同的，合理设计壳内结构，使其能够有效阻断振动波的传递，进而起到减振降噪的作用。因此研究基座对双层圆柱壳振动特性的影响对其减振降噪有重要意义。

虽然通过波动理论来分析结构中振动波传递是非常准确的，但是对于一个复杂的结构要分析波的多向传播和耦合以及能量流的多通道传递是非常困难的。因此在工程实际中一般采用数值仿真与模型试验相结合的方法进行复杂结构的振动特性分析[3-4]。以往的典型船体结构波动特性分析都是局限在半无限结构假设基础上，但这对有限尺度的基座连接结构阻波特性分析具有很大的局限性。因此，本文在其他文献的基础上分析了有限尺度的“L”形和“”形连接结构的波动特性，探索了结构边界对振动波传递的影响规律。在此基础上，以某一双层圆柱壳动力舱段为例，通过数值实验及大尺度模型试验分析了不同基座结构连接形式对双层圆柱壳振特性的影响规律，旨在为舰船基座结构声学设计提供参考。

2 有限尺度基座连接结构波动特性分析

2.1 有限长板“L”形连接结构

分析构成“L”形连接的两块板为有限长时的振动波传递特性，以更加接近于实际结构。假设两块板长度分别为l1，l2，且两板长度远大于板内结构波波长，有限长板“L”形连接结构简图如图1所示，平面简谐弯曲波从x=-l1垂直入射板1。

与半无限长板构成的“L”形连接结构不同的是，当板为有限长时，入射波在转角处产生的透射和反射波在沿着板1，2传递到x=-l1和y=l2时，会再次被反射，而反射波会作为新的入射波入射转角，当板结构阻尼很小时，振动波会在板1，2中来回反射及透射。因此，直接从振动微分方程求解两板内结构波的质点振动速度将变得十分复杂。由于虚数波不传递能量；共轭衰减波成对出现，能量相互抵消，本文着重探索有限尺度的连接结构在转角处的实数波的传播特性。

当一平面简谐弯曲波从x=-l1垂直入射时，两板的质点振速可以看成为沿两板±x和±y两方向传递的结构波的质点振动速度的合成[5]:

图1 “L”形基座连接结构简图Fig.1 The structure of L junction base

式中:上标+表示沿两板正方向（板1中为沿+x，板2中为沿+y）传递的全部二次波和入射波在x=-l1或y=0合成质点振速，上标-表示沿两板负方向（板1中为沿-x，板2中为沿-y）传递的全部二次波和入射波在x=0或y=l2合成质点振速。

利用半无限长板“L”形连接结构在转角处的平衡关系和结构波在x=-l1、y=l2处的反射系数[6-7]，建立边界处和转角处的质点振速平衡方程:

1）在 x=-l1处:

2）在 y=l2处:

3）在转角处:

下午丁主任再也不敢到柜台前站了，他总是在他老婆坐的木桩上看报纸，看书，有时，看到梨花出来解手，也打声招呼，可看到后面鬼鬼祟祟地跟着潘美丽，便埋头看自己手里的东西，头都不抬。潘美丽走过去，一把拿下他手里的东西：你的眼水还不错哈！丁主任笑笑，看着远方：去上班吧。潘美丽等着梨花走远了才在丁主任头上一拍，身后丢下一句：别吃着碗里的，看着锅里的。

式中VBI表示在x=-l1处入射弯曲波质点振速；下表附加了-l1和-l2的反射系数分别表示结构波在x=-l1和y=l2处的反射系数。

将（1）-（4）式联立，就可得到一个八元线性方程组，将方程组写成矩阵形式:

图2 有限长“L”形结构弯曲波透射系数频域曲线Fig.2 Bending wave transmission coefficient of limited scale L junction structure

图3 有限长“L”形结构弯曲波反射系数频域曲线Fig.3 Bending wave reflection coefficient of limited scale L junction structure

当入射弯曲波VBI已知后，通过求解方程组，就可求得边界处及转角处的质点振动速度（i=1，2），最后得到两板内的质点振动速度的分布。假设两板的材料为钢，长度都为10 m，厚度也都为0.01 m，图2和图3为透射效率、反射效率系数随频率变化曲线。从图2和图3可以看出，当组成“L”形连接结构的板为有限长时，其各系数都随着频率的变化而发生振荡变化，而不是像无限长板那样是一条光滑曲线，这是由于当板结构为有限长后，板端存在反射，振动波在边界和转角处来回反射而导致的；同时也可以看出，τBB和ρBB两系数都在随频率的增大其整体趋势逐渐变小。

将各反射系数和透射系数相加，即 τBB+τBL+ρBB+ρBL，图4为各系数之和随频率变化曲线。

从图4中可以看到:在部分频率处各系数之和大于1，这是由于有限长板边界处和突变截面处都存在反射，在某些频率处，当波在有限长结构中来回反射时，两板中将产生驻波甚至发生共振，从而使得振动能量在两板中“富集”，导致各系数之和大于1。

图4 有限长“L”形结构各能量传递系数系数之和频域曲线Fig.4 The sum of sound coefficient of limited scale L junction structure with frequency

2.2 阶梯形连接结构中振动波传递分析

在有限长“L”形连接结构的振动波传递特性分析基础上，本小节推导了阶梯型（“”形）连接结构中振动波传递特性。如图5所示的“”形连接结构，其可以看成是由两个“L”形连接结构延拓而来的。当平面弯曲波垂直入射第一个直角接头时，由于不均质结构中存在波型变换，因此当入射第二个直角接头时既有弯曲波又有转化的纵波。假设各板相对应的长度分别为l1，l2，l3。

忽略边界处的近场效应，当一列平面简谐弯曲波垂直入射后，板内质点的振动速度可以看作是沿±xi方向传递的振动波的质点振速的合成:

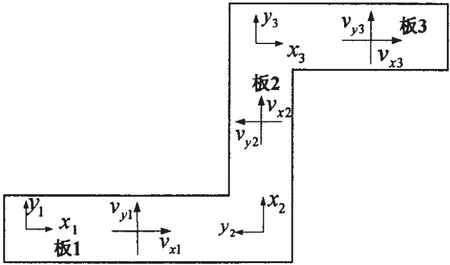
图5 “”形基座结构简图Fig.5 The structure of junction base

由于板1和板3的边界处有:

将突变截面从左至右依次编号为1，2。利用前几节推导的突变截面处平衡条件，则第i（i=1～3）块板的振动波质点振动速度在突变截面处的平衡方程为:

式中:反射系数下脚标编号表示第i（i=1，2，3）个板在向其他波传递振动波的反射系数，如rBL12表示板1向板2传递振动波时弯曲波—纵波转换的反射系数，其他类同。

将（6），（7）式和（8）式联立，得到一个关于质点横向及纵向振动速度的线性方程组，将其写成矩阵形式:

图6 板1到板3弯曲波传递系数频域曲线Fig.6 Sound transmission coefficient of bending wave with frequency

图7 板1到板3衍生纵波传递系数频域曲线Fig.7 Sound transmission coefficient of derivation longitudinal wave with frequency

从图6和图7中可以看出，无论是弯曲波—弯曲波透射效率还是弯曲波—纵波透射效率，其曲线随频率都有很大的变化，在一系列极大与极小值之间来回振荡，这是由于从板1向板3的振动波传递能量主要取决于板2中沿x2正方向传递的结构波的幅值（包括由板1透射进入板2的以及沿x2负方向传递至第一转角处反射而产生的二次振动波总和），当在某一些特定频率下，透射结构波与全部二次反射波相位相同，从而使得振动波沿x2正方向传递的振动波幅值相互叠加而达到极大值，使得透射效率达到最大值，甚至超过1，而在另一些频率下，透射结构波与全部二次反射波相位正好相反，从而使得沿x2正方向传递的振动波幅值相互抵消，使得透射效率达到最小值。

对比图2和图6可以看出:在10-3000 Hz的艇体机械噪声主导频带内，“”形连接结构的弯曲波透射效率除个别频点外较“L”形结构显著降低，具有高传递损失特性。

3 基座连接形式对艇体振动特性的影响规律

在考虑双层圆柱壳减振降噪时，也可以从壳内基座出发，通过改变基座结构连接形式，构造高传递损失基座，从而降低双层圆柱壳振动声辐射。

因此，在双层圆柱壳典型基座的设计布置上可以采用透射效率较低的连接结构替代透射效率较高的连接结构，从而阻断振动波的传递。在满足GJB4000-2000前提下，在满足结构强度及稳定性基础上开展了基座结构参数优化设计，根据舱段结构参数结果将基座腹板与基座安装板之间移开一段距离50 mm，构造“”形连接结构的基座结构，其结构简图如图8所示。

图8 “L”形基座转换为“ ”形基座Fig.8 The sketch base structure junction

为了考察基座对振动的影响，在圆柱壳耐压壳结构和储油舱舱壁结构上选取9个考核点，由于结构左右对称，考核点位置位于模型左侧，其考核点布置如图9所示。

图9 舱段结构简图及测点布置Fig.9 The sketch of power cabin and measuring points

建立有限元模型以及边界元模型，其中在建立流体介质水时，为了保证计算精度，流体介质水场半径取4倍双层圆柱壳轻外壳半径[8-9]。按照满足最大计算频率（500 Hz）进行网格划分，图10为双层圆柱壳有限元及边界元模型，以内部含旧基座模型为例。

在基座面板中间施加单位载荷力，通过有限元软件ABAQUS计算结构的振动，然后将轻外壳的振动响应作为边界条件，采用边界元软件VIRTUALLAB软件中的直接边界元方法计算其声辐射[10]。

图10 FEM/BEM耦合法计算模型Fig.10 Calculation model with FEM/BEM method

图11为基座连接形式改变前后轻外壳振动均方速度随频率的变化曲线。

上面分析了基座连接结构改进前后舱段非耐压壳体的振动特性，下面深入分析基座—液舱壁—非耐压壳体的主传递途径中各典型测点的振动特性。图12为基座形式改变前后典型测点处的振动加速度级的频率响应曲线。

图11 轻外壳振动均方速度级频响曲线Fig.11 Comparative curves of vibration acoustic level of outer shell

图12 典型测点振动加速度级频响曲线Fig.12 Comparative curves of vibration acoustic level at typical measuring points

从图12中可以看出:在大部分频率点处，将基座连接形式由“L”形转换为“”形后，各测点振动加速度有不同程度减小；将基座连接形式改变后，振动峰值向高频发生转移，且共振峰值个数明显变少。表1为各测点平均减振效果，从表1中可以看出，各测点都能够有效降低壳体振动，振动加速度级平均减振约2.0 dB。

表1 基座连接形式改进前后舱段测点10-500 Hz频段减振效果表Tab.1 The 10-500 Hz variation acoustic level with different connection types

4 大尺度动力舱段模型振动试验验证

在哈尔滨工程大学振动冲击实验室完成了双层圆柱壳空气中振动实验，实验分两种工况:1）“L”形连接基座（改进前）；2）“?”形连接基座（改进后），分别测量两种连接形式基座下典型测点处的振动加速度值，考察其减振效果。实验模型为某艇舱段缩尺比模型，由于实验模型基本为左右对称结构，实验过程中只是模型基座连接形式发生了变化，因此，为了降低实验成本且在不影响实验精度的情况下，将两个不同的基座形式置于同一个模型结构内，即模型壳内左舷为改进后基座，模型壳内右舷为改进前基座。本次实验模型为实验模型结构示意图如图13所示，图14为实验模型实物图。

图13 实验模型结构示意图Fig.13 The sketch of experiment model

图14 实验模型实物图Fig.14 Practical object of the experiment model

双层圆柱壳模型的内壳和外壳上都有环肋，壳体间由多块托板连接，耐压壳内部左右两舷各有一燃油舱，在燃油舱水平舱壁上安装有基座，在图13中，1—轻外壳；2—外壳环肋；3—托板；4—内壳环肋；5—耐压壳；6—上层建筑壳板；7—上层建筑横梁；8—液舱顶板；9—液舱纵壁板；10—液舱支撑结构；11—改进后基座；12—改进前基座；13—端板。从图14（b）中可以明显看出壳内基座结构连接形式。

分别在动力原舱段推进电机基座面板及声学设计后基座面板中心处激励，激励力为10-1000 Hz白噪声，对测试数据进行归一化处理，从而分析得到基座下液舱壁、耐压壳体上的振动特性。测点布置左右对称，其振动加速度计布置与数值试验相同。图15给出基座连接结构改进前后液舱壁典型测点加速度级频响曲线。

图16为结构声学设计前后耐压壳体典型测点加速度级频响曲线。

图15 基座连接结构改进前后液舱壁典型测点加速度级频响曲线Fig.15 Comparative curves of vibration acoustic level at tank wallafter

图16 基座连接结构改进前后耐压壳体典型测点加速度级频响曲线Fig.16 Comparative curves of vibration acoustic level at inner shell

从表2中可以看出，基座连接结构改进前后动力舱段耐压壳体的中高频段的振动得到了有效的衰减和隔离。舱段耐压壳体在10-1000 Hz频段振动加速级平均降低约3 dB。由此可见，艇体基座连接结构在进行声学改进后，有效地阻抑了基座—液舱壁—耐压壳的结构声的主传递通道。

表2 基座连接结构改进前后舱段各测点10-1000 Hz频带减振效果列表Tab.2 The 20-1000 Hz variation acoustic level with different connection types

续表2

5 结 论

本文基于波动理论的分析处理方法，探索了有限尺度的“L”形和“”形连接结构的波动特性，探索了结构边界对振动波传递的影响规律。以某一双层圆柱壳动力舱段为例，通过数值试验对比分析了不同基座结构连接形式对双层圆柱壳振动特性的影响规律。在此基础上开展了大尺度模型的振动试验测试，得到以下结论:

[1]尼基福罗夫 阿 斯.船体结构声学设计[M].北京:国防工业出版社,1998.

[2]刘见华.舰船结构声传递的阻抑机理及应用研究[D].上海:上海交通大学博士学位论文,2003.

[3]Cemer L,Heckl M,Ungar E E.Structure-borne Sound[M].Second Edition.Berlin:Springer-Verlag,1988:316-334.

[4]车驰东,陈端石.成任意角度连接的两块平板转角处阻振质量对平面弯曲波传递的影响分析[J].声学学报,2007,32(3):282-288.

[5]Grice R M,Pinnington R J.A method for the vibration analysis of built-up structures,Part I:Introduction and analysis of the plate-stiffened beam[J].Journal of Sound and Vibration,2000,230(4):825-849.

[6]Mitri F G,Fellah Z E A.Acoustic radiation force on coated cylinders in plane progressive waves[J].Journal of Sound and Vibration,2007,308:190-200.

[7]Wu G X,Eatock Taylor R.The coupled finite element and boundary element analysis of nonlinear interactions between waves and bodies[J].Ocean Engineering,2003,30:387-400.

[8]Ji Fang,Yao Xiongliang.The influence of blocking mass parameters to power cabin vibration isolation performance[J].Journal of Marine Science,2010,1:11-17.

[9]计 方,姚熊亮.舰船高传递损失基座振动波传递特性研究[J].工程力学,2011,3:240-245.

[10]Yao Xiongliang,Ji Fang.Attenuation of the flexural wave transmission through impedance mismatch hull base[J].Journal of Ship Mechanics,2010,15(6):678-689.