基于焓平衡法的固体燃料冲压发动机燃速预示模型①

谢爱元，武晓松，夏 强，2

(1.南京理工大学机械工程学院，南京 210094;2.北京临近空间飞行器系统工程研究所，北京 100067)

符号说明:

0 引言

固体燃料冲压发动机工作状态与发动机外弹道参数、进气道工作性能、发动机结构尺寸及固体燃料物理化学性质等息息相关。在发动机设计与分析中，对固体燃料燃面退移速率进行预示，有助于优化发动机结构尺寸，提高燃烧效率、增大比冲;与发动机内弹道模型及进气道工作状态模型结合，还可优化发动机工作状态。

固体燃料冲压发动机的燃面退移速率(简称燃速)不仅和固体燃料、燃烧室结构尺寸有关，还和来流条件、燃料/空气的化学当量比有关［1－4］。目前，解决这一问题的方式主要通过大量的实验研究［2－4］，总结出燃面退移速率的经验公式，成本高昂。然而，这些经验公式均忽略了装药长度对燃面退移速率的影响;当所设计的工况不在以往实验工况范围内时，通过插值外推所得到的数据可能产生很大的误差;且该方法对于新配方的固体燃料无效。

文献［5］基于流场与固体药柱间传热的焓平衡，建立了中小尺寸的混合火箭燃面退移速率模型，编写了计算程序，预示了2个不同尺寸的HTPB/N2O混合火箭内弹道，并与实验数据进行了对比，证明了该模型的准确性，但没有给出具体的计算流程。

在文献［5］的基础上，本文假定工作过程中固体燃料壁面温度不是初温(通常为300 K)，而是固体燃料的汽化温度(聚乙烯为 430 K、HTPB 为 480 K［6］等);同时，计算从初温到汽化温度过程中固相吸收的热量。考虑装药长度及来流空气总温的变化对退移速率的影响，建立固体燃料冲压发动机固体燃料的退移速率模型，联合计算热力学软件CEA，编写燃面退移速率预示程序。

1 燃面退移速率模型

固体燃料冲压发动机的物理模型如图1所示。在固体燃料内表面的单位面积上存在焓平衡，关系式如下:

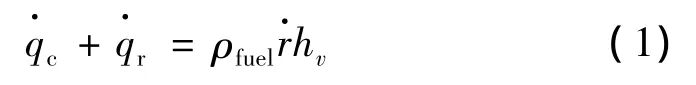
方程(3)中，对流换热系数可由斯坦顿数St表示，如下:

使用雷诺修正/科尔伯恩分析法［7］，可将斯坦顿数表示为

将方程(4)、(5)代入方程(3)，得

上述只适合于无汽化的混合壁面边界，燃料汽化的质量加入边界模型由Lees［8］提出，表述如下:

式(8)为长度方向上不同位置处，固体药柱燃面退移速率的计算方程。

固体燃料冲压发动机药柱通道内的流动为管流。从再附着点开始，其边界层将不断发展，直到形成完全发展的管流为止。其药柱的长径比通常小于20，在药柱通道内，完全发展的湍流并未建立。因此，基于完全发展管流的对流换热经验公式并不适用。

为解决这一问题，本文使用基于平板扰流边界层理论而得的表面摩擦因子经验公式，Mottard和Loposer［9］的实验，证实了将其用于未充分发展管流的可靠性。

表面摩擦因子表示如下［7］:

式(9)的使用范围为106＜Rex＜108，适用于固体燃料冲压发动机。

将式(9)在长度方向上取平均值得到平均摩擦因子:

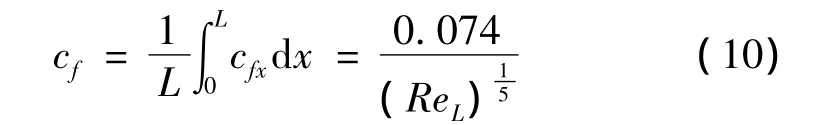
在固体燃料冲压发动机中，来流空气质量通量ρeUe可表示为

本文使用CEA进行热力学计算，所得参数为对应工况下轴向上的平均值。同时，与来流空气质量流率相比，燃气质量流率很小(约为0.1)，将其忽略，认为轴向上气体的密流处处相等。

将式(10)、式(11)带入式(8)中，可得长度方向上燃面退移速率的平均值。

由此可见，当其他参数不变时，固体燃料的平均退移速率正比于装药长度L的－0.2次方。燃料的质量流率可表示为

对于给定的氧化剂/燃料混合物，其燃烧状态的影响因素有环境压力、氧化剂/燃料的质量之比、氧化剂/燃料的初温等。而最大的影响因素为氧化剂/燃料的质量之比，表示如下:

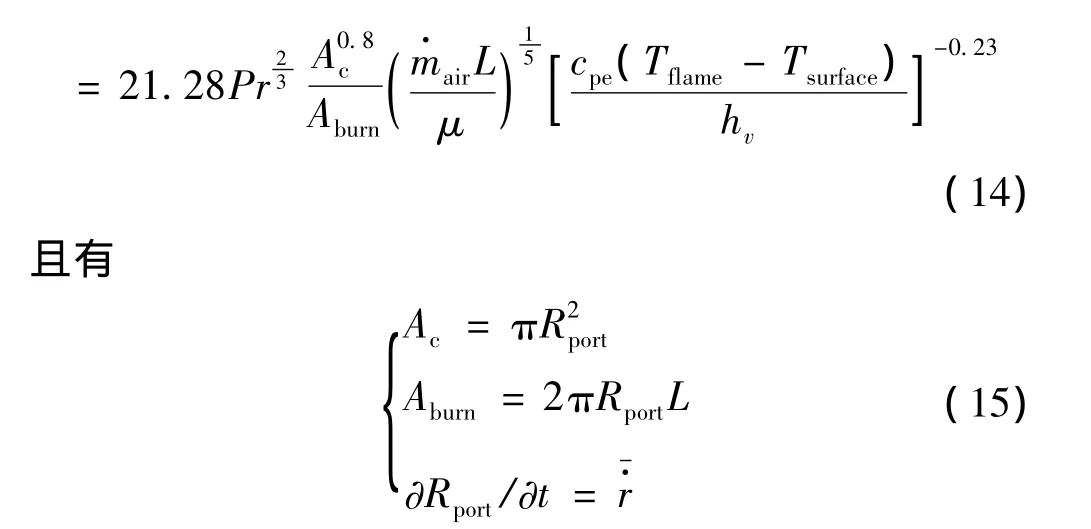
发动机中燃烧生成的热量，一部分用于加热反应物，一部分被产物带走。文献［5］中，使用N2O和HTPB作为氧化剂和固体燃料，其化学当量比为1时，氧化剂与燃料的质量之比为8.95。气态N2O的定压比热约为0.9 kJ/kg，HTPB 的固相比热容为 2.38 kJ/kg，即化学当量比为1时，温度升高1 K，N2O与HTPB的吸热量之比约为3.4。由于汽化吸热，喷入燃烧室的气态N2O的初温很低(0.1 MPa下，N2O的汽化温度为185 K)，而固体推进剂的初温为300 K。由此可见，在N2O/HTPB的混合火箭中，可忽略HTPB固相由初温至汽化温度的吸热量，认为固体燃料的内壁温度为初温。而固体燃料冲压发动机中，来流空气温度较高(Ma=3时为840 K，直连式实验中一般大于450 K)，此时固体燃料由初温至汽化温度的吸热量是不能忽略的。文中假定固体燃料的内壁温度为其汽化温度。

对给定固体燃料，从初始温度的固相变为气相，吸收的热量可表示为

联式立(12)～式(16)，即可获得燃面退移速率。

至此，对于不同的固体燃料，只需掌握其密度、有效汽化热、汽化温度、固相比热容及其汽化后的组分等数据，通过联合CEA计算热力学软件计算其汽化产物与空气燃烧产物的温度及输运系数，通过迭代求解出固体燃料的燃面退移速率。

2 燃面退移速率计算

2.1 碳氢聚合物的热解产物

碳氢聚合物的分解是一系列复杂的物理化学过程，其分解产物与其表面温度密切相关。本文假设固体燃料 PMMA、PE的热解产物分别为单体 MMA(C5H8O2)［1］和 C2H4。

2.2 影响燃面退移速率的参数选取及计算流程

国内外大量文献表明，固体药柱燃面退移速率受药柱通道直径、燃烧室压强、来流空气质量流率、总温等因素影响。文献［4］表明，在低压下(pc＜0.8 MPa)，固体燃料燃烧时几乎没有颗粒生成，辐射换热量可忽略，燃烧室压强变化对燃面退移速率的影响很小;0.8 MPa≤pc≤1.3 MPa时，颗粒生成量随压强增大而增多，进而辐射换热量增大，此时，燃烧室压强变化对燃面退移速率的影响不可忽略;pc＞1.3 MPa后，颗粒生成量已饱和，辐射换热量不变，燃面退移速率再次与压力无关，但辐射换热不可忽略。文献［1］表明，，可见低压下，燃烧室压强增大100%时，燃面退移速率仅增大14.6%。本文所计算的工况均在0.8 MPa以下，因此仅考虑药柱通道直径、来流空气质量流率、总温对燃面退移速率的影响。

图2为0.7 MPa下，不同来流温度Tair，燃烧产物状态随混合比的变化关系，其中MMA的标准生成焓为－340.53 kJ/mol［1］。只考虑对流换热的情况下，PE 的有效汽化热为4.0～5.5 MJ/kg，其值取得越大，数值仿真结果与实验结果越吻合［2］。因此，文中取PE的有效汽化热为5.5 MJ/kg;PMMA的有效汽化热为2.0 MJ/kg［6］。PE 与 PMMA 的密度分别为 965 kg/m3和1 180 kg/m3，固相比热容为2.0 kJ/kg 和1.0 kJ/kg［6］。固体燃料冲压发动机中常用由温升定义的燃烧效率ηΔT来表征固体燃料的燃烧效率。文献［1，4］表明，成功点燃的固态碳氢燃料，ηΔT平均值约为0.9，部分可达0.95，本文取 ηΔT=0.9 作为 PMMA、PE 的燃烧效率。

计算流程如图3所示。其中，计算步长为0.005～0.05 s，收敛准则为固体燃料质量消耗率的初判值与二次判断值误差小于0.5%。

2.3 计算结果与分析

本文对PE(PMMA)为燃料的固体燃料冲压发动机燃面退移速率共进行了23次计算，结果如表1所示。其中，文献［3］拟合的公式，燃面退移速率与压强pc有关，计算其退移速率的试验值时，取pc=7 atm(本文计算产物物性时选取的压强)。表1中，数据来源为燃速公式一栏中所对应的参考文献，误差为负时表示燃面退移速率的计算值小于试验值，“—”表示此项无内容。

由表1可知，当燃料为PE时，除了来流空气总温Tair=300 K外，其计算值与实验值的误差均在±15%以内，误差绝对值的平均值为5.63%。

当其他条件不变时，Tair由300 K变化至700 K时，计算误差逐渐减小，由正变负。固体燃料冲压发动机中，燃烧主要受扩散火焰控制，温度越高，分子间的扩散运动越剧烈，在有限时间内分子间的混合越充分，即来流空气总温越高，固体燃料冲压发动机燃烧效率越高。同时，文献［1］表明，来流空气总温为300 K时，固体燃料点燃后，很快熄灭，燃烧并不能稳定。因此，Tair=300 K时，计算误差偏大的主要原因为ηΔT的取值过高;取ηΔT=0.5时，计算结果见表1(修正后一列)，可知误差均在0～15%以内。这表明了该模型的一致性和可靠性。

表1 计算结果Table 1 Calculated results

燃料为PMMA，Tair=423 K时，计算误差均为负值，原因为实验中使用航空煤油/氧气燃烧加热来流空气的直接加热方式，航空煤油燃烧并不完全，使得来流空气中含有大量的碳颗粒，辐射换热不可忽略。以PMMA为燃料的固体燃料冲压发动机中，当有大量碳颗粒时，辐射换热量为对流换热量的15%［10］，即式(1)中=0.15。

考虑辐射后，Tair=423 K时，燃面退移速率的计算值分别为 0.302、0.373、0.227 mm/s，对应误差为5.0%、4.6%和 －14.3%，均在 ±15%以内。

同时，由表1还可发现，其他条件不变时，来流空气质量流率增加，计算误差也由大变小，由正变负。这是因为来流空气质量流率的增加，导致空气的流动速度加快，提高了空气/燃料的混合速率，使得实际燃烧效率从低于0.9逐渐变化到高于0.9。修正后，PE计算误差绝对值的平均值为7.8%，PMMA计算误差绝对值的平均值为6.55%。

表2为同一工况下，不同装药长度的燃面退移速率计算结果。对其进行指数拟合，结果为

与式(12)相符合，造成差异的原因为工作过程中随着燃面退移速率的降低，空燃比增大，火焰温度、燃烧产物的物性不断改变。

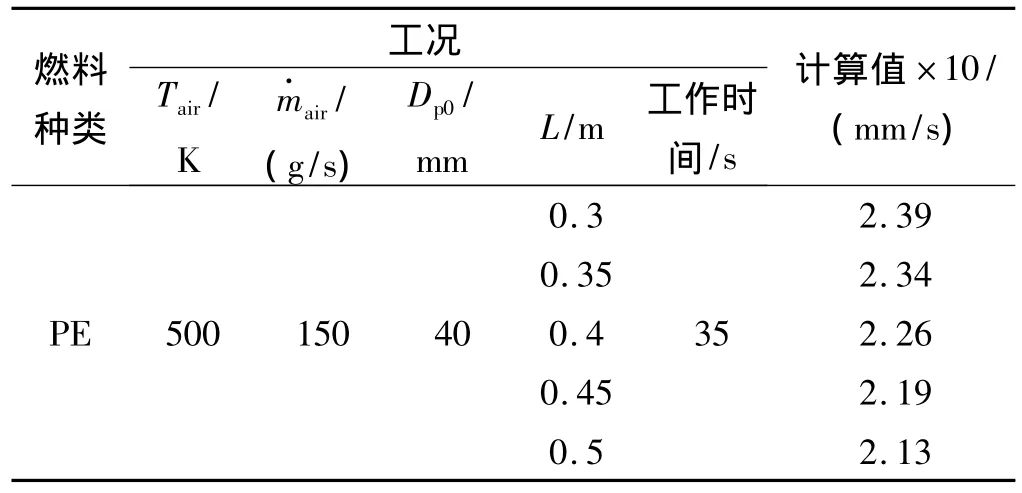
表2 不同装药长度燃面退移速率的计算结果Table 2 Regression rate calculated results with length change of fuel

3 结论

(1)当来流空气总温Tair≥423 K时，取燃烧效率ηΔT=0.9，计算值与试验值吻合很好，误差均在±15%以内。

(2)对于PE，当来流空气总温Tair=300 K时，ηΔT=0.9，计算值与试验值不吻合。其主要原因为燃烧效率取值过大，选取合理的燃料效率值后，计算值与试验值吻合，误差在0～15%。

(3)其他条件不变时，提高来流空气质量流率，有利于空气/燃料的混合，提高燃烧效率。

(4)来流空气总温为450 K以上时，PE计算误差绝对值的平均值为5.63%;PMMA计算误差绝对值的平均值为6.55%，所建立的模型准确可靠。

(5)计算结果表明，当其他参数不变的情况下，固体燃料冲压发动机中燃面退移速率与装药长度的－0.23次方成正比，这是首个将装药长度考虑在内的固体燃料冲压发动机燃面退移速率模型。

［1］夏强.固体燃料冲压发动机工作过程研究［D］.南京:南京理工大学，2011.

［2］Elands P J M，Korting P A O G.Combustion of polyethylene in a solid fuel ramjet－a comparison of computational and experimental results［R］.AIAA 88－3043.

［3］Schulte G.Fuel regression and flame stabilization studies of solid－fuel ramjets［J］.Journal of Propulsion and Power，1986，4(2):301－304.

［4］Korting P A O G，Van C W M，Der Geld.Combustion of PMMA in a solid fuel ramjet［R］.AIAA 86－1401.

［5］Shannon D Eilers，Stephen A Whitmore.Correlation of hybrid rocket propellant regression measurements with enthalpy－balance model predictions［J］.Journal of Spacecraft and Rockets，2008，5(45):1010－1020.

［6］Timnat Y M，Korting P A O G.Hybrid rocket motor experiments［R］.Department of Aerospace Engineering，Delft University of Technology，Report LR－452，1985.

［7］Incropoera F P，Dewitt D P，et al.传热和传质基本原理［M］.葛新石，等译.北京:化学工业出版社，2009.

［8］Lees L.Convective heat transfer with mass addition and chemical reactions［C］//Combustion and Propulsion，3rd AGARD Colloquium，Pergamon，New York，1958:451.

［9］Mottard E J，Loposer J D.Average skin－friction drag coefficients from tank tests of a parabolic body of revolution［R］.NACA RP－1161，1957.

［10］Michael E Metochianakis，David W Netzer.Modeling solidfuel ramjet combustion，including radiation to the fuel surface［J］.Journal of Spacecraft Technology，1983，4(15):405－406.