基于模糊集理论与CSMR的岩质边坡稳定性分析

李云，刘霁,

(1. 湖南城市学院 测绘与市政工程学院，湖南 益阳，413000；2. 中南大学 资源与安全工程学院，湖南 长沙，410083)

边坡失稳产生的灾害是最为严重的地质灾害之一，特别是随着大量开采业、水利水电业、公路业的不断发展，期滑坡现象日益严峻[1]，边坡的稳定性分析与评价显得非常重要，许多研究者进行了大量研究[2-6]。岩质边坡的稳定性受众多复杂因素影响[7]，是一个包含大量不确定信息并且难于用数值表示的问题，稳定性分析结果又依赖于这些因素。Romanam[8]以比较合理的工程地质和岩石力学背景，在RMR法的基础上提出 SMR评价方法，我国水电系统的工程技术人员对在对 SMR评价方法进行修正的基础上提出了 CSMR评价方法。无论是 SMR评价方法还是CSMR评价方法，都不能很好地处理影响因素数据的模糊性，而模糊集理论非常适宜于处理这些具有不确定性的因素。为此，本文作者将模糊集理论与CSMR评价方法相结合对岩质边坡稳定性进行评价。

1 CSMR评价方法

CSMR分类体系(Chinese system of SMR)是以SMR评价方法为基础提出的改进的边坡总体稳定性评价方法。SMR评价方法是在RMR法的基础上增加4个修正指标，CSMR法在SMR基础上再增加2个修正系数，所以，RMR法是CSMR系统的基础，也是岩质边坡稳定性评价的重要工具。

1.1 RMR岩体评价方法

RMR分类体系见表1。RMR方法是Bieniawski[9]提出的,该体系考虑了岩石的单轴抗压强度(RUCS)或点载荷强度、岩石质量指标(RRQD)、节理间距(RSD)、节理条件(RCD)和地下水(RGD)等因素对岩体质量的影响RRMR：

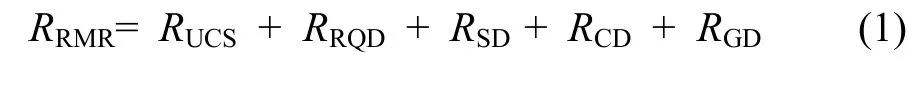
式中：RCD为节理条件评分值；RBG为地下水评分值；RRMR为岩体质量的影响评分值。

1.2 SMR评价方法

Romana于1985年引入考虑节理和边坡相互关系的系数的SMR系统，提出4个新的修正指标：F1反映结构面倾向与边坡倾向的关系；F2反映平面滑动中结构面倾角的影响；F3反映边坡倾角与结构面倾角的关系；F4反映开挖方法对边坡稳定的影响[10]。

表 2所示为修正指标 F1，F2，F3和 F4的取值原则，表3所示为根据SMR评分方法对边坡稳定性的评价分类。

1.3 CSMR评价方法

中国水利水电工程边坡登记小组通过对大量实际工程的对比分析，提出了引入高度修正和结构面条件修正的CSMR体系[11]。CSMR指标的计算公式为

式中：ξ为高度修正系数；λ为结构面性质折减系数；RCSM为边坡总体稳定性评价值。结构面条件修正系数λ按表4确定，高度修正系数ξ按下式确定：

表1 RMR分类参数及评价标准Table 1 Parameters of RMR and evaluation standard

表2 修正指标及取值原则Table 2 Adjusting factors for discontinuity

表3 SMR法边坡稳定性评价表Table 3 Empirical description of SMR classes

表4 结构面条件修正系数λTable 4 Discontinuity condition adjusting coefficient λ

式中：H为边坡高度；H0为标准高度，建议取 H0=80 m。

2 模糊集理论

模糊集是扎德于1965年提出的，这一概念源自于经典集合理论。经典的集合理论认为任何1个元素与任何1个元素的关系只有“属于”与“不属于”2种情况，绝对不允许模棱两可。模糊集把普遍集合中的元素对集合隶属度只能取0和1，推广到可以取区间[0,1]上的任意1个数值[12]。实现模糊逻辑推理的过程主要有3步：模糊化、模糊推理和解模糊化，见图1。

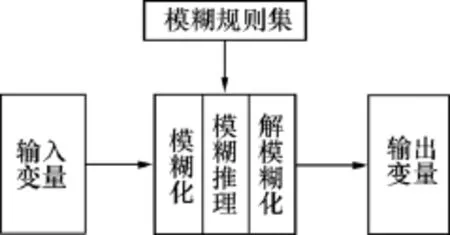
图1 模糊推理系统Fig.1 Fuzzy inference system

2.1 模糊化

模糊化过程把输入的精确量转换为相应的模糊集合，这样才能用输入值作为模糊控制规则中的条件来运用模糊规则进行推理。为了实现模糊化，先要进行论域变换，将真实论域变换为内部论域，并要针对输入语言变量定义模糊子集及其隶属度函数。

2.2 模糊推理

通过一组模糊条件语句构成模糊控制规则，并计算模糊控制规则决定的模糊关系，然后根据推理合成规则进行模糊推理。在该步，输入语言变量被加到 1个IF-THEN规则的集合中，把各种规则的结果加在一起产生1个“模糊输出”集合。IF-THEN规则可以表示为：

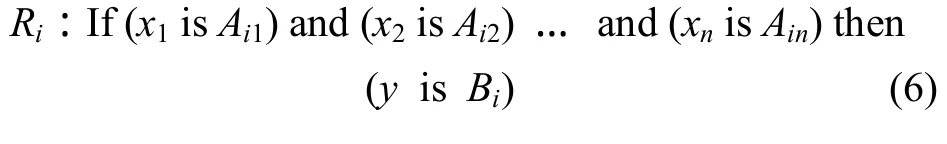
其中：Ri表示第i条控制规则；(x1, x2, …, xn)表示输入变量；y表示控制变量；(Ai1, Ai2, …, Ain)为隶属度函数uAij(xj)定义的模糊推理；Bi为规则的结论[13]。

模糊推理是应用模糊关系表示模糊条件句，将推理的判断过程转化为对隶属度的合成及演算过程，即已知模糊命题，推出新的模糊命题作为结论的过程。模糊推理系统是基于模糊集理论和 IF-THEN规则的运算系统，既可以处理精确的输入，也可以处理模糊的输入，因此，模糊推理系统广泛应用于自动控制、数据分类处理、分析决策和专家系统等方面。在实际应用中，常见的模糊推理系统主要有3种：Mamdani模糊模型、Tsukamoto模糊模型和Takagi-Sugeno-Kang模糊模型，它们的主要区别是模糊规则和解模糊化过程不同。常用的推理方法有Zadeh推理方法、Mamdani推理方法和模糊加权推理法[14]，而Mamdani推理方法在模糊逻辑中最常见。Mamdani认为模糊集和模糊逻辑可以用于将非结构化的语言描述转化成运算法则，而很多地质学上的参数是用语言来描述的，因此，Mamdani推理方法适宜于复杂的工程地质问题的处理，本文也采用Mamdani推理方法。

2.3 解模糊化

通过模糊推理得到的结果是1个模糊集合或者隶属度函数，但在实际应用中，往往需要1个确定值。解模糊化过程就是在推理得到的模糊集合中取1个最能代表这个模糊集合单值的过程，最常见的精确化方法包括最大隶属度函数法、重心法和加权平均法。在实际中应用最多的是重心法，它的优势在于所有的隶属度函数都参与了精确化过程。

3 基于模糊集理论的CSMR评价方法

在本文中，模糊推理模型有6个输入和2个输出，共有 300条模糊规则。在模糊推理过程中采用Mamdani推理方法，采用重心法解模糊化过程。由于CSMR法是在RMR法和SMR法基础上修正的，因而，按照模糊集理论对各个因素进行重组，最终形成的FCSMR流程见图2。图中：UCS为单轴抗压强度值；RQD为岩石质量指标值；SD为节理间距；CD为节理条件值；GD为地下水评分值；F1为结构面与边坡倾向的关系值；F2为平面滑动中结构面倾角值；F3为边坡倾角与结构面倾角的关系值；F4为开挖方法对边坡稳定性的影响值。

3.1 RMR模糊系统

RMR模糊系统用于计算RMR评分值，本来应该有5个输入和1个输出，但是，由于节理条件和地下水条件没有明确的数值而难于计算，因此，RMR模糊系统只涉及岩石单轴抗压强度、岩石质量指标和节理间距3个因素。当系统解模糊化完成时，直接将另外2个因素的评分值加到模糊系统的输出评分值上。RMR模糊推理系统输入参数的隶属度函数见图3。

图2 FCSMR系统流程图Fig.2 Flow chart of FCSMR

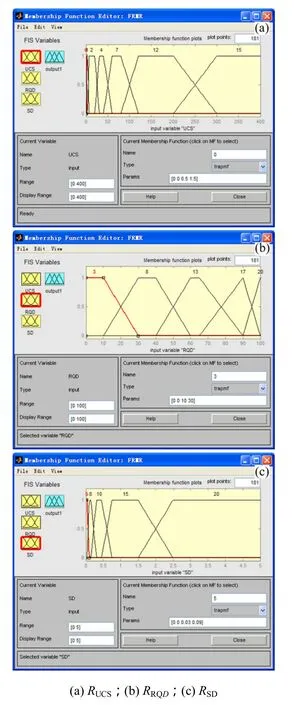
图3 RMR模糊系统输入参数Fig.3 Input parameters of RMR fuzzy inference system

3.2 修正指标的模糊系统

在4个修正指标中，边坡的开挖方法属于语言性描述而不是1个确定值，因此，将F1，F2和F3作为输入参数，F4直接加到解模糊化得到的结果上。修正指标模糊系统参数的隶属度函数见图4。

3.3 边坡稳定性FCSMR评价

将 RMR模糊系统和修正指标模糊系统得到的评分值按式(3)计算得到最终的FCSMR评分值，FCSMR评分值的模糊分级见图5。

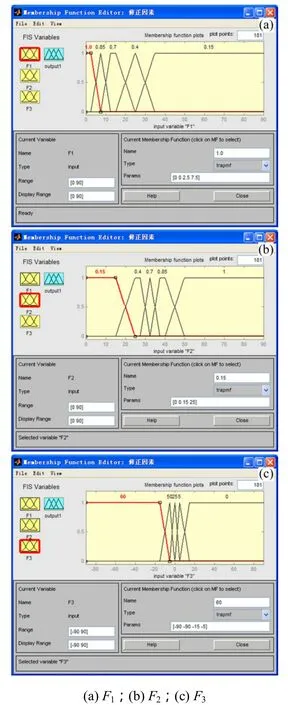
图4 修正指标的模糊系统输入参数Fig.4 Input parameters of adjusting factors fuzzy inference system

图5 FCSMR分值的隶属度函数Fig.5 Membership functions of FCSMR

4 FCSMR工程应用

4.1 工程概况

大朝山水电站进水口位于澜沧江右岸冲沟龙塘沟右侧，进水口边坡所在的山坡为1个凸起地形，两面临空，山脊走向约30°，坡角约为45°，整个边坡高约为120 m。主要岩性为三叠系上统的火山喷出岩，岩层为单斜构造，流层产状变化较大，一般为310°～350°∠16°～34°。地质调查表明，进水口边坡区无Ⅰ和Ⅱ结构面，主要发育4组节理，这4组节理的产状见表5。

进水口边坡岩石风化强烈，全强风化带底界为10～20 m，微风化带底界为60～130 m，强风化带岩体风化卸荷裂隙发育，岩体呈散体或碎裂结构，岩体强度低，节理裂隙充填物多为次生泥。边坡的 RMR法评价结果见表6。

表5 主要节理参数Table 5 Main discontinuities characterization parameters

4.2 边坡稳定性评价

根据表5和表6，利用FCSMR系统对边坡进行评分，得到最终评分值为19.7。由表3可见：边坡稳定性极差，会发生平面滑动或类似土质滑坡。从图 7可以看出：边坡的FCSMR分值同时属于Ⅴ级和Ⅳ级。根据CSMR评分系统得到边坡的评分值为27.2，边坡稳定性很差；CSMR分值属于Ⅳ级，会发生大规模平面滑动或楔形体滑动。这 2种评价方法对比结果见表7。

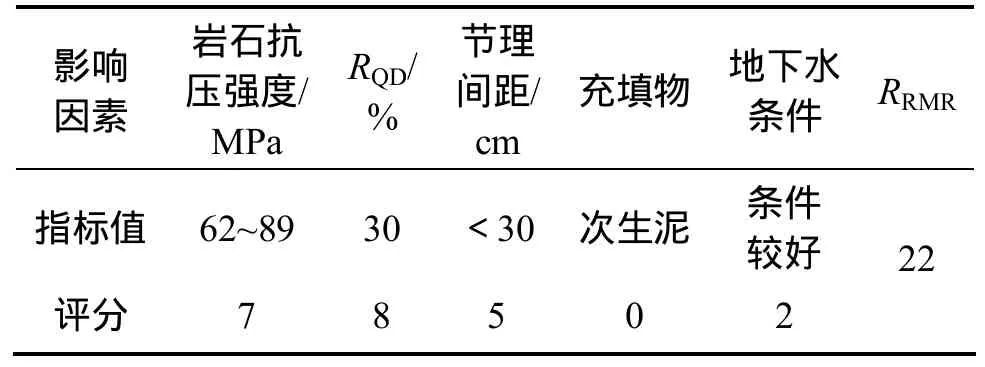
表6 RMR评价结果Table 6 RMR parameters and rating

表7 FCSMR与CSMR评价结果Table 7 Evaluation results of FCSMR and CSMR

为了验证FCSMR评价方法是否正确，利用理正岩土边坡稳定性分析系统计算边坡的安全系数作为验证标准，为此，首先计算岩体的内聚力c和内摩擦角φ。在一定围压范围内，广义Hoek-Brown准则能表示成破坏面上正-剪应力的形式，用于Mohr-Coulomb准则中抗剪强度参数的估算[15]。最终估算结果见表8。

表8 边坡岩体抗剪强度参数Table 8 Shear strength parameters of slope rock mass

按照表7中的Mohr-Coulomb参数，利用岩土边坡稳定性分析系统，计算边坡的安全系数。按照圆弧形滑动方式，采用瑞典条分法计算得到的安全系数为1.493，按照平面滑动方式计算得到的安全系数为1.918。理正软件计算结果表明：边坡发生圆弧形类似土质滑坡的可能性更大，FCSMR评定结果更加接近于实际情况，即边坡可能发生类似土质滑坡。这也同时证明FCSMR评价方法是准确、可靠的。

5 结论

(1) 由于组成岩质边坡的岩体的性质、组织结构不同，以及岩体中结构面发育情况存在差异，导致地下水状况不同。基于岩质边坡的稳定性评价过程是一个处理数据模糊性的过程，将模糊集理论引入岩质边坡稳定性评价中。

(2) 对大朝山水电站进水口边坡进行稳定性评价时，CSMR评价评价方法得分值为27.2，可能发生平面破坏或楔形体破坏，评分值属于Ⅳ级；而 FCSMR评价方法评分值为19.7，边坡可能发生平面破坏或类似土质滑坡，评分值同时属于Ⅴ级和Ⅳ级。根据理正岩土边坡稳定性分析系统的计算结果，边坡按照圆弧形破坏计算得到的安全系数为1.493，按平面破坏计算得到的安全系数为1.918，即边坡发生圆弧形滑动即类似土质滑坡的可能性更大，FCSMR评价方法评价结果比CSMR评价方法评价结果更加准确、可靠。

(3) 将模糊集理论与CSMR评价方法相结合，是评价岩质边坡稳定性的一种有效方法。

[1] 薛锦春, 李夕兵, 董陇军. 边坡稳定性的聚类未确知综合识别方法及应用[J]. 岩土力学, 2010, 31(Z1): 293-297.XUE Jing-chun, LI Xi-bing, DONG Long-jun. Study of rock slope stability based on clustering uncertained measurement complicated algorithm[J]. Rock and Soil Mechanics, 2010,31(Z1): 293-297.

[2] 李文秀, 梁旭黎, 赵胜涛. 地下水影响下裂隙岩质边坡变形的 Fuzzy测度分析[J]. 岩石力学与工程学报, 2005, 24(2):302-306.LI Wen-xiu, LIANG Xu-li, ZHAO Sheng-tao. Fuzzy measures analysis for displacements and deformations of jointed rock slope under influence of groundwater[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(2): 302-306.

[3] 雷远见, 王水林. 基于离散元的强度折减法分析岩质边坡稳定性[J]. 岩土力学, 2006, 27(10): 1693-1698.LEI Yuan-jian, WANG Shui-lin. Stability analysis of jointed rock slope by strength reduction based on UDEC[J]. Rock and Soil Mechanics, 2006, 27(10): 1693-1698.

[4] 徐卫亚, 蒋中明, 石安池. 基于模糊集理论的边坡稳定性分析[J]. 岩土工程学报, 2003, 25(4): 409-413.XU Wei-ya, JIANG Zhong-ming, SHI An-chi. Slope stability analysis using fuzzy sets theory[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(4): 409-413.

[5] 马毅, 王希良, 刘振, 等. 基于模糊因素的岩质边坡地震稳定性多模型组合评价[J]. 岩土力学, 2011, 32(Z1): 624-629.MA Yi, WANG Xi-liang, LIU Zhen, et al. Multiple model combination evaluation of seismic stability of rock slopes based on fuzzy factors[J]. Rock and Soil Mechanics, 2011, 32(Z1):624-629.

[6] 冯树荣, 赵海斌, 蒋中明. 节理岩体边坡稳定性分析新方法[J]. 岩土力学, 2009, 30(6): 1639-1642.FENG Shu-rong, ZHAO Hai-bin, JIANG Zhong-ming. A new method of stability analysis of jointed rock slop[J]. Rock and Soil Mechanics, 2009, 30(6): 1639-1642.

[7] 张晓晖, 王辉, 戴福初, 等. 基于关系矩阵和模糊集合的斜坡稳定性综合评价[J]. 岩石力学与工程学报, 2000, 19(3):346-351.ZHANG Xiao-hui, WANG Hui, DAI Fu-chu, et al.Comprehensive evaluation of slope stability using interaction matrix and fuzzy sets[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(3): 346-351.

[8] Romanam. New adjustment ratings for application of Bieniawski classification to slopes[C]//International Symposium on the Role for Rock Mechanics. Zacatecas: ISRM, 1985: 49-53.

[9] Bieniawski Z T. Engineering classification of joint rock masses[J]. The Civil Engineer in South Africa, 1973, 15(12):335-343.

[10] 邱恩喜, 谢强, 石岳, 等. 修正 SMR 法在红层软岩边坡中的应用[J]. 岩土力学, 2009, 30(7): 2109-2113.QIU En-xi, XIE Qiang, SHI Yue, et al. Application of modified SMR to redbed soft rock slopes[J]. Rock and Soil Mechanics,2009, 30(7): 2109-2113.

[11] 孙东亚, 陈祖煜, 杜伯辉, 等. 边坡稳定评价方法 RMR-SMR体系及其修正[J]. 岩石力学与工程学报, 1997, 16(4): 297-304.SUN Dong-ya, CHEN Zu-yu, DU Bo-hui, et al. Modifications to the RMR SMR system for slop stability evaluation[J]. Chinese Journal of Rock Mechanics and Engineering, 1997, 16(4):297-304.

[12] 闻新, 周露, 李江东, 等. MATLAB模糊逻辑工具箱的分析与应用[M]. 北京: 科学出版社, 2001: 37-46.WEN Xin, ZHOU Lu, LI Jiang-dong, et al. Analysis and application of MATLAB fuzzy logic toolbox[M]. Beijing:Science Press, 2001: 37-46.

[13] 陈乐求, 彭振斌, 陈伟, 等. 基于模糊控制的人工神经网络模拟在土质边坡安全预测中的应用[J]. 中南大学学报: 自然科学版, 2009, 40(5): 1381-1387.CHEN Le-qiu, PENG Zhen-bin, CHEN Wei, et al. Artificial neural network simulation on prediction of clay slope stability based on fuzzy controller[J]. Journal of Central of South University: Science and Technology, 2009, 40(5): 1381-1387.

[14] 周润景, 张丽娜. 基于MATLAB与fuzzy TECH的模糊与神经网络设计[M]. 北京: 电子工业出版社, 2010: 73-87.ZHOU Run-jing, ZHANG Li-na. Fuzzy and neural network design based on MATLAB and fuzzy TECH[M]. Beijing:Electronics Industry Press, 2010: 73-87.

[15] 李远耀, 殷坤龙, 代云霞. 基于广义Hoek-Brown准则强度折减法的岩坡稳定性分析[J]. 岩土力学, 2008, 29(Z1): 347-352.LI Yuan-yao, YIN Kun-long, DAI Yun-xia. Stability analysis of rock slope by strength reduction method based on generalized Hoek-Brown failure criterion[J]. Rock and Soil Mechanics, 2008,29(Z1): 347-352.